Презентация по математике "Проектная работа: Гиперкуб"

Цель: систематизировать теоретические знания о фигуре четырехмерного пространства и создать слайд-фильм.

Гипотеза: если четырехмерное пространство существует, то в этом пространстве можно представить геометрические фигуры и предположить их практическое применение.

Объект: теоретические знания научно- популярной литературы и материалы Интернета.

Предмет: фигура четырехмерного пространства.

Определение гиперкуба

Гиперкубом называется правильный политоп, ячейкой которого является куб.

Политоп – это четырехмерная фигура, граница которой состоит из многогранников. Аналогом ячейки политопа является грань многогранника. Гиперкуб является аналогом трехмерного куба. Эта фигура также известная под названием тессеракт.

 Слово было образовано от греческого "τεσσερες ακτινες" ("четыре луча"), имеется в виде четыре оси координат. Кроме этого, в некоторых источниках, эту же фигуру называли тетракубом (tetracube).

Гиперкуб имеет 16 вершин, 32 ребра, 24 грани (квадрата), 8 ячеек (кубов). Из каждой вершины исходят по четыре взаимно-перпендикулярных ребра. Границей гиперкуба является трехмерная замкнутая выпуклая фигура, объем которой (боковой объем гиперкуба) равняется восьми единичным трехмерных кубам. Внутри себя эта фигура содержит единичный гиперкуб, гиперобъем которого равняется гиперобъему единичного гиперкуба.

Мы не можем представить себе вещь, существующую вне трёх пространственных измерений и одномерной временной протяжённости. Может быть после соответствующей тренировки, когда в результате эволюции ум человеческий превратится в более мощный инструмент, мы и смогли бы научиться мыслить в четырёх пространственных измерениях. Сейчас мы этого не умеем. Мы смотрим на мир сквозь пространственно-временные очки, одно стекло которых позволяет нам воспринять одномерное время, другое – трёхмерное пространство. Мы не можем представить себе мысленно образ гиперкуба или какой-нибудь другой четырёхмерной структуры. М. Гарднер "Этот правый, левый мир"

Вот так мы видим Гиперкуб в развернутом виде в трехмерном пространстве

Полную информацию смотрите в презентации.

Почему наше пространство трёхмерно?

И. Кант

"Размышления об истинной оценке живых сил" (1747)

Выполнили:

ученики 10-В класса

Матвеев Дмитрий , Пилипенко Иван

Руководитель:

Божова С.В.

учитель математики

• Цель: c истематизировать теоретические знания о фигуре четырехмерного пространства и создать слайд-фильм.
• Гипотеза: если четырехмерное пространство существует, то в этом пространстве можно представить геометрические фигуры и предположить их практическое применение.
• Объект: теоретические знания научно-

популярной литературы и

материалы Интернета.

• Предмет : фигура

четырехмерного пространства.

• Гиперкубом называется правильный политоп, ячейкой которого является куб.
• Политоп – это четырехмерная фигура, граница которой состоит из многогранников. Аналогом ячейки политопа является грань многогранника. Гиперкуб является аналогом трехмерного куба. Эта фигура также известная под названием тессеракт.
• Слово было образовано от греческого " τεσσερες ακτινες " ("четыре луча"), имеется в виде четыре оси координат. Кроме этого, в некоторых источниках, эту же фигуру называли тетракубом (tetracube).

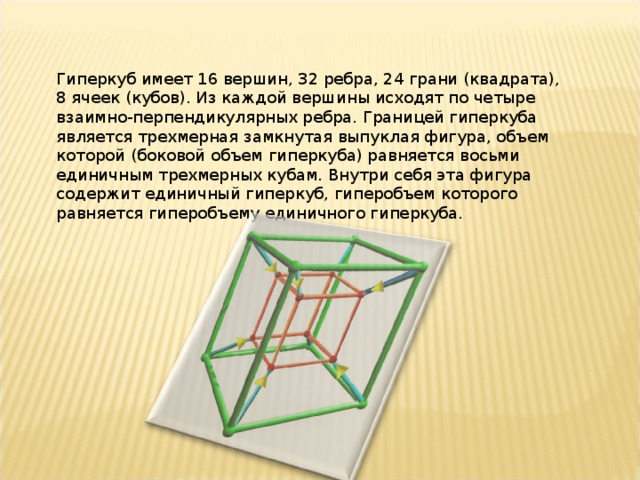
Гиперкуб имеет 16 вершин, 32 ребра, 24 грани (квадрата), 8 ячеек (кубов). Из каждой вершины исходят по четыре взаимно-перпендикулярных ребра. Границей гиперкуба является трехмерная замкнутая выпуклая фигура, объем которой (боковой объем гиперкуба) равняется восьми единичным трехмерных кубам. Внутри себя эта фигура содержит единичный гиперкуб, гиперобъем которого равняется гиперобъему единичного гиперкуба.

0-мерный куб

Начнём с начала — с 0-мерного куба. Этот куб содержит 0 взаимно перпендикулярных граней, то есть это просто точка.

1-мерный куб

В одномерном пространстве у нас есть только одно направление. Сдвигаем точку в этом направление и получаем отрезок.

Это одномерный куб.

• 2-мерный куб
• У нас появляется второе измерение, сдвигаем наш одномерный куб (отрезок) в направлении второго измерения и получаем квадрат.

• Это куб в двумерном пространстве.
• 3-мерный куб
• С появлением третьего измерения поступаем аналогично: сдвигаем квадрат и получаем обычный трёхмерный куб.

4-мерный куб -

Теперь у нас появилось четвёртое измерение. То есть в нашем распоряжении имеется направление, перпендикулярное всем трём предыдущим. Воспользуемся им точно так же. Четырёхмерный куб будет выглядеть вот так.

Естественно, трёхмерный и четырёхмерный кубы нельзя изобразить на двумерной плоскости экрана. Это проекции.

• Четырехмерное пространство есть упорядоченное множество точек M(x; y; z; t). Для задания гиперкуба нужно определить координаты шестнадцати его вершин:
• A(0; 0; 0; 0), B(1; 0; 0; 0), C(1; 1; 0; 0), D(0; 1; 0; 0),
• E(0; 0; 1; 0), F(1; 0; 1; 0), G(1; 1; 1; 0), H(0; 1; 1; 0),
• K(0; 0; 0; 1), L(1; 0; 0; 1), M(1; 1; 0; 1), N(0; 1; 0; 1),
• O(0; 0; 1; 1), P(1; 0; 1; 1), R(1; 1; 1; 1), S(0; 1; 1; 1).
• Координаты гиперкуба получены из координат трехмерного куба добавлением четвертой координаты, равной нулю, а потом единице.
• Используя формулы аналитической геометрии

для четырехмерного евклидового пространства,

можно получить свойства гиперкуба.

• Р ассмотрим геометрическую модель гиперкуба. Как мы получаем геометрическую модель трехмерного куба? Мы делаем его развертку, а из развертки «склеиваем» модель куба. Развертка трехмерного куба состоит из квадрата, к сторонам которого приложено по квадрату плюс еще один квадрат. Примыкающие квадраты поворачиваем вокруг сторон квадрата, соседние стороны квадратов соединяем друг с другом , а оставшиеся четыре стороны замыкаем последним квадратом

• Аналогично рассмотрим развертку гиперкуба. Его разверткой будет являться трехмерная фигура, состоящая из исходного трехмерного куба, шести кубов, примыкающих к каждой грани исходного куба и еще одного куба. Всего восемь трехмерных кубов. Чтобы из данной развертки получить четырехмерный куб (гиперкуб), нужно повернуть на 90 градусов каждый из прилегающих кубов. Эти прилегающие кубы будут расположены в другом трехмерном пространстве. Соседние грани кубов соединить друг с другом. Вложить восьмой куб гранями в оставшееся незаполненное пространство. Получим четырехмерную фигуру – гиперкуб, граница которого состоит из восьми трехмерных кубов. Существует 261 различная развёртка тессеракта

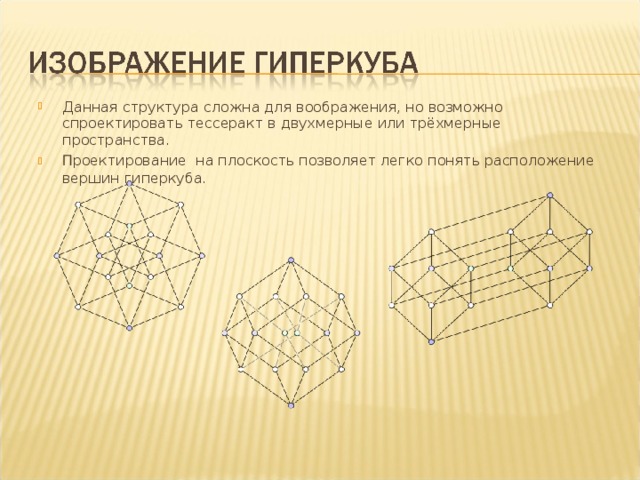
• Данная структура сложна для воображения, но возможно спроектировать тессеракт в двухмерные или трёхмерные пространства.
• П роектирование на плоскость позволяет легко понять расположение вершин гиперкуба.

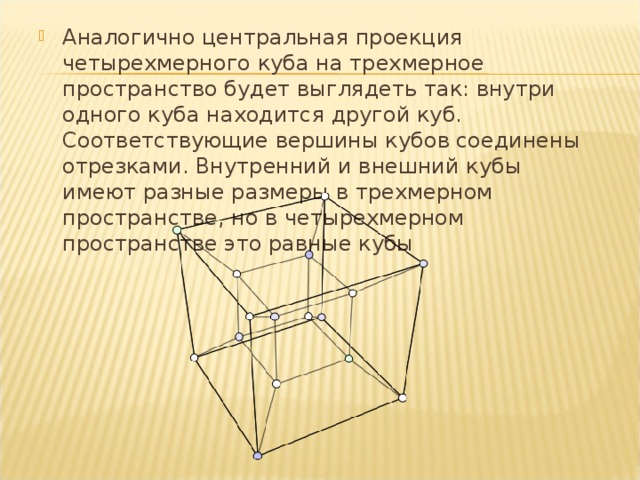
• Аналогично центральная проекция четырехмерного куба на трехмерное пространство будет выглядеть так: внутри одного куба находится другой куб. Соответствующие вершины кубов соединены отрезками. Внутренний и внешний кубы имеют разные размеры в трехмерном пространстве, но в четырехмерном пространстве это равные кубы

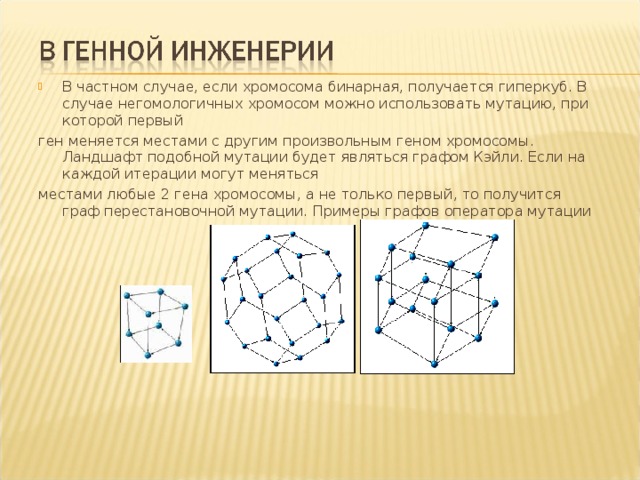
• В частном случае, если хромосома бинарная, получается гиперкуб. В случае негомологичных хромосом можно использовать мутацию, при которой первый

ген меняется местами с другим произвольным геном хромосомы. Ландшафт подобной мутации будет являться графом Кэйли. Если на каждой итерации могут меняться

местами любые 2 гена хромосомы, а не только первый, то получится граф перестановочной мутации. Примеры графов оператора мутации

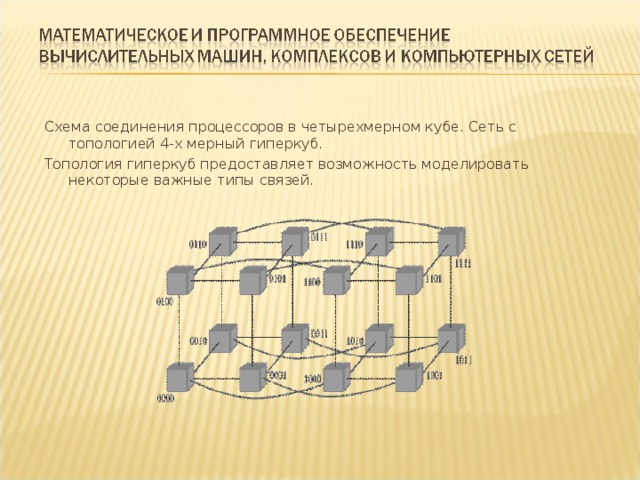
Схема соединения процессоров в четырехмерном кубе. Сеть с топологией 4-х мерный гиперкуб.

Топология гиперкуб предоставляет возможность моделировать некоторые важные типы связей.

Витражное изображение гиперкуба, выполненное архитектором Клодом Брегдоном в 1913 г. для Торговой палаты Рочестера. Видны четыре наклонных куба, два вертикальных и два горизонтальных. 21 октября на математическом факультете Университета штата Пенсильвания состоялось открытие необычной скульптуры под названием "Октакуб". Она представляет собой изображение четырёхмерного геометрического объекта в трёхмерном пространстве. По мнению автора скульптуры, профессора Адриана Окнеану, столь красивой фигуры такого рода в мире не существовало, ни виртуально, ни физически, хотя трёхмерные проекции четырёхмерных фигур изготавливались и раньше."Октакуб" был изготовлен из нержавеющей стали в инженерных мастерских Университета штата Пенсильвания. Установлена скульптура в отремонтированном корпусе имени Макаллистера математического факультета. Высота, ширина и длина скульптуры одинаковы и составляют около 180 см. Размещена скульптура на гранитном пьедестале высотой 90 см так, чтобы её центр находился примерно на уровне взгляда человека.

• Гиперкуб появился в научно-фантастической литературе с 1940 года, когда Роберт Хайнлайн в рассказе "Дом, который построил Тил" описал дом, построенный по форме развертки тессеракта. В рассказе этот дом сворачивается, превращаясь в четырехмерный тессеракт. После этого гиперкуб появляется во многих книгах и новеллах.
• В фильме "Куб 2: Гиперкуб" рассказывается о восьми людях, запертых в сети гиперкубов.
• На картине Сальвадора Дали "Распятие" ("Crucifixion (Corpus Hypercubus)", 1954) изображен Иисус распятый на развертке тессеракта. Эту картину можно увидеть в Музее Искусств (Metropolitan Museum of Art) в Нью-Йорке.

В данной работе ставилась цель дать первоначальное знакомство с четырехмерным пространством. Сделано это было на примере самой простой фигуры – гиперкуба.

Мир четырехмерного пространства удивителен! В нем, наряду с похожими фигурами в трехмерном пространстве, существуют и фигуры, аналогов которых нет в трехмерном пространстве.

Многие явления материального мира, макромира и мегамира, несмотря на грандиозные успехи в физике, химии и астрономии, так и остались необъяснимыми.

Познав свойства четырехмерного пространства и позаимствовав некоторые идеи из четырехмерной геометрии, можно будет не только построить более строгие теории и модели материального мира, но и создать инструменты и системы, функционирующие по законам четырехмерного мира, тогда возможности человека окажутся еще более впечатляющими.

В ходе работы мы:

1. Изучили научно-популярную литературу и материалы Интернета по данной теме.

2. Осуществили обзорный анализ изученного материала.

3. На основе полученного материала создали слайд-фильм.

Мы считаем, что наша работа поможет учащимся старших классов получить наглядное представление по данной теме, и считаем , что своей работой вносим значительный вклад в повышение мотивации к самостоятельному изучению геометрии и понимании ее практической значимости.