
УРОК – ПРЕЗЕНТАЦИЯ. ТЕМА : Определение геометрической прогрессии. Формула n -го члена геометрической прогрессии

ЦЕЛЬ УРОКА :
- Формирование понятия геометрической прогрессии, используя сопоставление и противопоставления понятию арифметической прогрессии.
- Познакомить со свойствами геометрической прогрессии и формулой n- го члена.
- Закрепить на примерах решения задач.

Задачи урока :
- Обучающие: ввести понятие геометрической прогрессии; развитие общеучебных умений и навыков. Развивающие: работа по овладению учебно-интеллектуальными умениями(сравнение, обобщение , исследование), расширение эрудиции по предмету. Воспитательные : создание комфортной атмосферы на уроке, привитие навыков самооценки, привитие интереса к предмету .

Содержание урока:
- Самостоятельная работа с проверкой в классе.
- Организация изучения понятия геометрической прогрессии и введение формулы n- го члена геометрической прогрессии.
- Первичное применение знаний и умений.
- Подведение итогов работы на уроке.

Самостоятельная работа

В заданиях 1-3 дана арифметическая прогрессия. Найдите: 1 вариант 2 вариант
- двадцать третий член, если первый член -9 и разность 4.
- сумму десяти первых членов, если а = 4 n +2 , n – натуральное число.
- сумму семи первых членов прогрессии
-5;-3;-1;…
4. Продолжите числовую последовательность, записав еще 2 члена: -2;6;-18;…
- тридцать второй член, если первый член 65 и разность -2.
- сумму десяти первых членов, если а = 3n-1, n – натуральное число.
- сумму семи первых членов прогрессии 8;4;0;…
- Продолжите числовую последовательность, записав еще 2 члена: 1;2;4;…

Ответы к самостоятельной работе:

Изучение понятия геометрической прогрессии и вывод формулы n -го члена геометрической прогрессии.

4 задание 1 вариант 2 вариант
1
1 2
2 2
4 2
8 2
-2
-2 ( -3)
6 ( -3)
-18 ( -3)
54 ( -3)

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число.

Исторические сведения.
- С геометрической прогрессией, которую получили в первом веке, связана интересная легенда. По преданию, шахматы были изобретены в пятом веке до нашей эры в Индии. Индусский царь был так восхищен игрой , что решил отблагодарить изобретателя шахмат. Который ,в свою очередь, попросил следующую награду: выдать ему за первую клетку

- шахматной доски одно зерно, за вторую клетку -2 пшеничных зерна, за третью-4, за четвертую-8, за пятую-16 зерен и т.д. до 64 клетки, т.е. за каждую следующую клетку доски следует выдавать в 2 раза больше, чем за предыдущую. Царь был недоволен просьбой, так как считал , что изобретатель, прося столь ничтожную награду , оскорбляет его. И тогда придворный математик стал считать ,сколько зерна должен получить изобретатель. Для того чтобы подсчитать величину награды , мы должны сложить все зерна, лежащие на всех клетках доски.



Для того чтобы подсчитать величину награды, надо сложить зерна, лежащие на всех клеточках доски.


- Когда подсчитали сумму зерен, то количество оказалось очень большим числом. Но такого количества зерна нет ни у какого царя, и просьбу изобретателя выполнить невозможно. А сегодня мы познакомимся с понятием геометрической прогрессии. Вспомните определение арифметической прогрессии и сформулируйте определение геометрической прогрессии.

Определение
Числовая последовательность отличных от нуля чисел, в которой каждый следующий член получается из предыдущего умножением на одно и тоже число q , называется геометрической прогрессией .
Числовая последовательность, в которой каждый следующий член получается из предыдущего прибавлением одного и того же числом d ,называется арифметической прогрессией .

Число d – называется разностью арифметической прогрессии.
Число q – называется знаменателем геометрической прогрессии.

Обозначение
Арифметическая прогрессия
Геометрическая прогрессия

Допустимые значения
Геометрическая прогрессия
числа неравные нулю
Арифметическая прогрессия
любые числа

Рекуррентная формула
Арифметическая
прогрессия
Геометрическая
прогрессия

Нахождение
разность арифметической
прогрессии
знаменатель геометрической прогрессии

Используя рекуррентную формулу, получим формулу общего члена геометрической прогрессии.
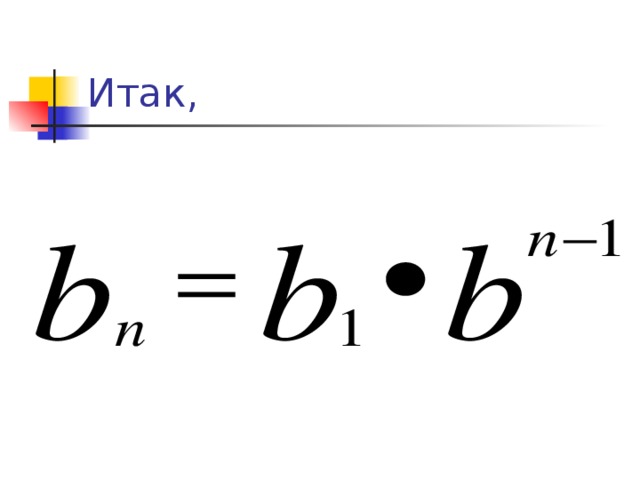
Итак,

Формула n- го члена
геометрическая
прогрессия
арифметическая
прогрессия

Характеристическое свойство
арифметическая
прогрессия
геометрическая
прогрессия
или

- Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних членов. Извлекая квадратный корень из обеих частей этого равенства, получим что для любых трех последовательных членов геометрической прогрессии выполняется равенство :
- Число, которое получилось в правой части равенства называется средним геометрическим двух чисел.

Числовая последовательность, в которой каждый следующий член получается из предыдущего прибавлением одного и того же числом d ,называется арифметической прогрессией .
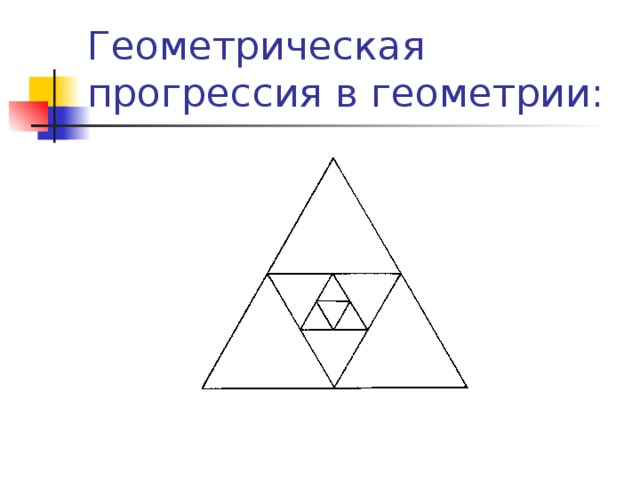
Геометрическая прогрессия в геометрии:

Решение задач

Задача 1
Найдите первые 5 членов
геометрической прогрессии , если
первый член -2, а знаменатель -0,5.
Ответ: -2; 1; -0,5; 0,25; - 0,125

Задача 2.
В правильный треугольник, сторона которого равна 16 см, вписан второй треугольник так, что его вершинами являются середины сторон первого. Во второй треугольник таким же способом вписан третий и т.д. Найдите периметр пятого треугольника.
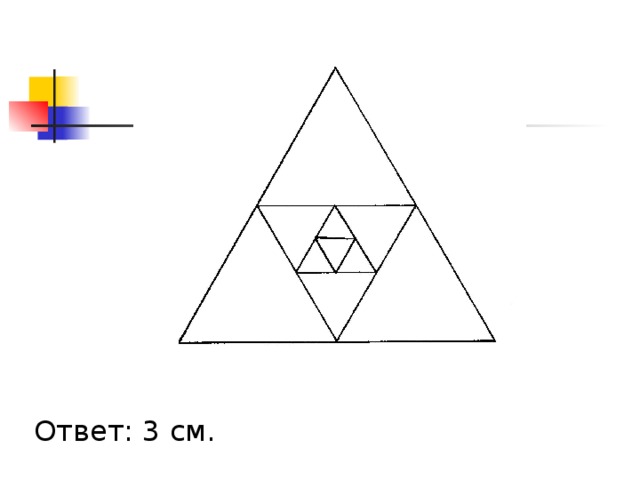
Ответ: 3 см.

Задача 3 (решить двумя способами)
Найдите знаменатель геометрической
прогрессии, если ее четвертый член
25, а шестой член 16.
Ответ:

Задача 4.
Между числами и 27 вставьте
четыре числа, чтобы получилась
геометрическая прогрессия.
Найдите эти числа.
Ответ: ; 1; 3; 9

Задача 5.
Дана геометрическая прогрессия ( ),
в которой и
Найти первый член геометрической
прогрессии.
Ответ: 12 или

Итог урока

Домашнее задание
- Придумать задачу, где используется геометрическая прогрессия.

Спасибо за урок!!!
До новых встреч!


 Получите свидетельство
Получите свидетельство Вход
Вход



























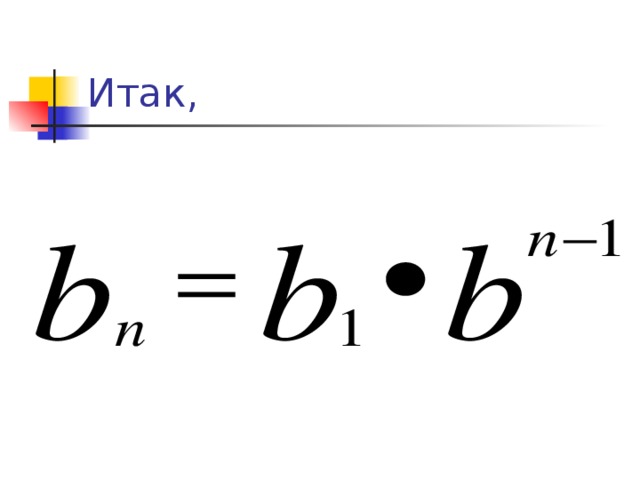
























 Презентация по математике "Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии" (3 MB)
Презентация по математике "Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии" (3 MB)
 0
0 681
681 14
14 Нравится
0
Нравится
0


