Цели урока:
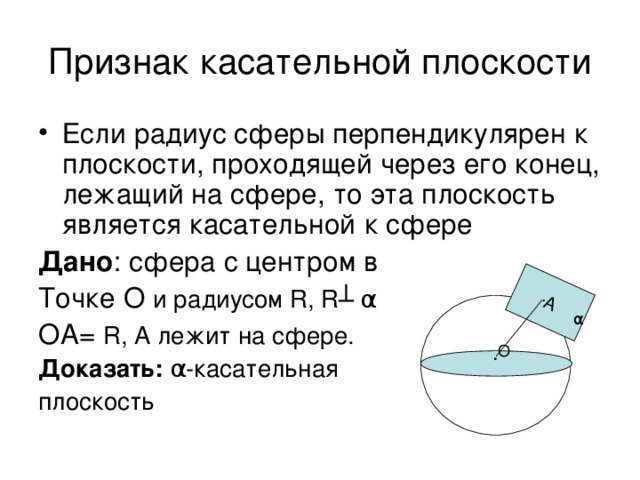
- рассмотреть теоремы о касательной плоскости к сфере;
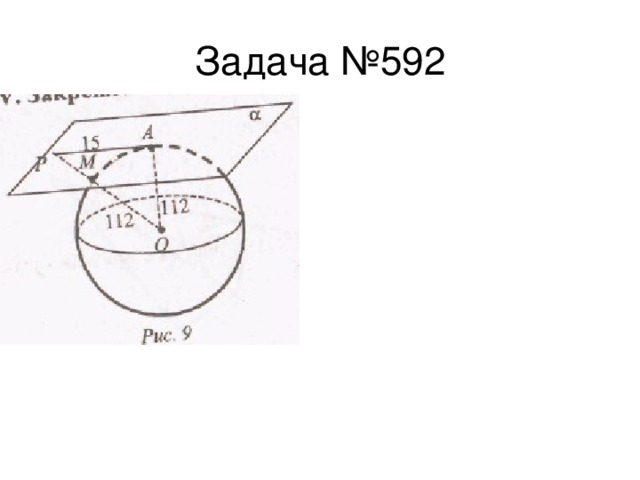
- научиться решать задачи по данной теме.
Устный опрос учащихся.
- Что называется сферой?
- Что называют диаметром сферы?
- Расскажите о взаимном расположении сферы и плоскости.
Изучение нового материала.

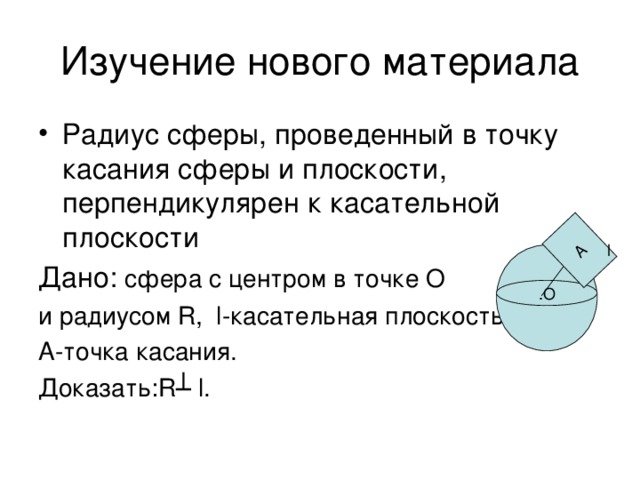
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости
Дано: сфера с центром в точке О и радиусом R, l - касательная плоскость,
А - точка касания.
Доказать: R┴ l.
Доказательство:

Предположим противное:
пусть R ┴ l, следовательно ОА – наклонная к плоскости l, значит, расстояние от центра, сферы до плоскости l меньше R=ОА:d< R, значит, сфера и плоскость l пересекает по окружности, что противоречит условию, что l-касательная плоскость, т.е. плоскость l и сфера имеют одну общую точку. Значит, R┴ l.


 Получите свидетельство
Получите свидетельство Вход
Вход



















 Презентация по математике "Касательная плоскость к сфере" (0.29 MB)
Презентация по математике "Касательная плоскость к сфере" (0.29 MB)
 1
1 2324
2324 553
553 Нравится
0
Нравится
0


