Готовимся к ОГЭ
УЧИТЕЛЬ МАТЕМАТИКИ
I КВАЛИФИКАЦИОННОЙ КАТЕГОРИИ
МБОУ ЛИЦЕЯ №12 г.ЛЕНИНОГОРСКА,
РЕСПУБЛИКИ ТАТАРСТАН:
ГАРЕЕВА ДИНА СЕРГЕЕВНА
Справочный материал
Справочный материал
Справочный материал
Справочный материал
Задача №9
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла А образует со стороной ВС угол равный 15 . Ответ дайте в градусах.
15
Е
В
С
ВЕА= ЕАD накрест лежащие углы
ЕАD= ВАЕ т.к. АЕ- биссектриса
А = 15 + 15= 30
15
15
А
D
Ответ: острый угол параллелограмма равен 30
Задача №9
В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠ B =133 ∠ D =173 . Найдите угол А. Ответ дайте в градусах.
Проведем диагональ АС
С
- АВС и ADC равнобедренные
С ADC равен А ADC , С AВC равен А AВC С = А четырехугольника АВСD, т.к. сумма всех углов четырехугольника равна 360 С + А= 360- (133+173)=54 С = А = 54:2=27
133
173
В
D
А
Ответ: А= 27
Задача №9
Сумма двух углов равнобедренной трапеции равна 50 0
Найдите больший угол трапеции. Ответ дайте в градусах
В
С
А+ D = 50
А= D = 50:2=25
В+ А=180 односторонние углы В= 180 – 25 =155
D
А
Ответ: больший угол трапеции равен 155
Задача №9
Найдите больший угол равнобедренной трапеции АВСD, если диагональ АС образует с основанием АD и боковой стороной АВ углы, равные 46 0 и 1 0 соответственно. Ответ дайте в градусах.
А= 46+1 =47
С
В
В+ А=180 односторонние углы В= 180 – 47 =133
1 0
46 0
А
D
Ответ: больший угол трапеции равен 133
Задача №9
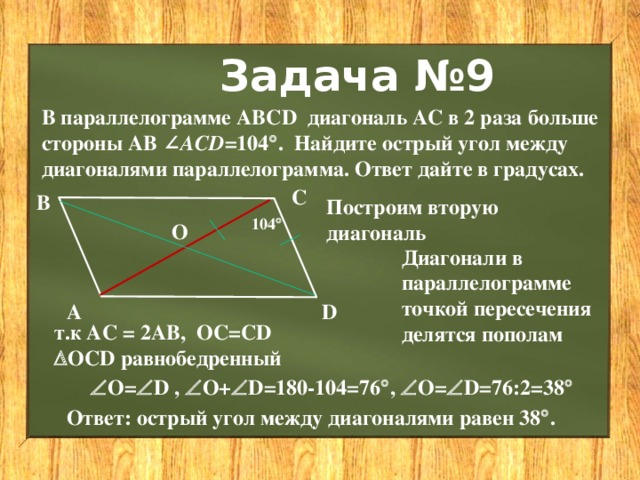
В параллелограмме АВСD диагональ AC в 2 раза больше стороны AB ∠ ACD =104 . Найдите острый угол между диагоналями параллелограмма. Ответ дайте в градусах.
С
В
Построим вторую диагональ
104
О
Диагонали в параллелограмме точкой пересечения делятся пополам
D
А
т.к АС = 2АВ, ОС=СD OCD равнобедренный
О= D , О+ D=180-104=76 , О= D=76:2=38
Ответ: острый угол между диагоналями равен 38 .
Задача №9
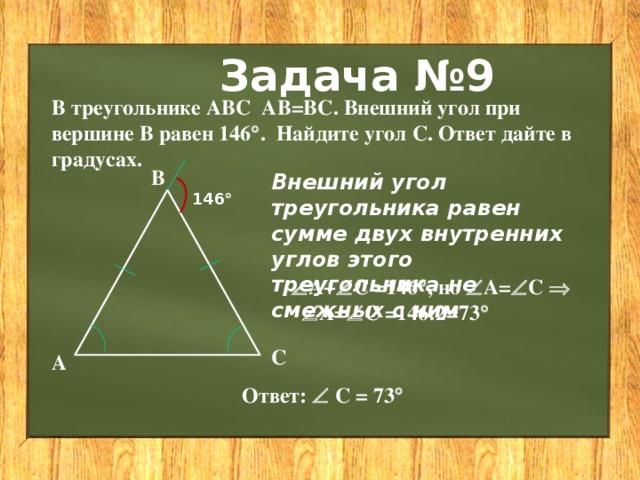
В треугольнике АВС АВ=ВС. Внешний угол при вершине В равен 146 . Найдите угол С. Ответ дайте в градусах.
В
Внешний угол треугольника равен сумме двух внутренних углов этого треугольника не смежных с ним
146
А+ С =146 , но А= С А= С =146:2=73
С
А
Ответ: С = 73
Задача №9
Точка О – центр окружности, на которой лежат точки А, В и С .Известно, что угол АВС равен 15 0 и угол ОАВ равен 8 0 Найдите угол ВСО. Ответ дайте в градусах.
.
АВС – вписанный угол, равен половине дуги на которую опирается АС=30 .
АОС=30 -центральный угол,
.
С
А
.
?
О
8 0
.
АОС= С 1 ОА 1 = 30 - вертикальные, т.е С 1 А 1 =30 , ВАА 1 – вписанный ВА 1 =16
15 0
А 1
С 1
16
в
- С 1 В=30-16=14 ;
- С 1 СВ- вписанный угол, опирающийся на С 1 В
С 1 СВ=14:2=7
Ответ: ВСО=7
Задача №10
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
4
В
С
КМ - средняя линия КВ=КА
КМ || ВС ВР=РD (по т.Фалеса)
КР – средняя линия ABD
КР=AD:2 = 10:2=5
Р
К
М
А
D
10
Ответ: больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей равен 5.
Задача №10
В равнобедренной трапеции известна высота, большее основание и угол при основании. Найдите меньшее основание.
Рассмотрим АВН он прямоугольный и равнобедренный, т.е. АН=ВН=5
В
С
5
Построим высоту из вершины С
А
45
D
СМD = АВН MD = AH = 5 AD = AH + HM + MD,
HM = BC
Н
М
14
BC = 14 – (5+5) = 4
Ответ: меньшее основание равно 4.
Задача №10
На окружности с центром О отмечены точки А и В так, что АОВ=66 . Длина меньшей дуги АВ равна 99. Найдите длину большей дуги.
.
Длина АВ= 99, но т.к. АОВ – центральный угол, опирающийся на АВ, АВ= 66 .
Тогда 1 = 99:66 =1,5
Большая АВ= 360 – 66 = 294
АВ= 294 · 1,5 = 441
В
.
99
.
О
66
А
Ответ: Большая АВ равна 441.
Задача №10
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Рассмотрим АОС он прямоугольный ОС=27, АС=36 применим т.Пифагора и найдем
.
27
С
72
О
А
ОА= 45 (радиус окружности)
D = 45 · 2 = 90
Ответ: диаметр окружности равен 90
Задача №10
Высота равнобедренной трапеции, проведённая из вершины С, делит основание AD на отрезки длиной 8 и 15. Найдите длину основания ВС.
В
С
АМВ= НСD HD = AM = 8
BC = MH = AH – AM = 15 – 8 = 7
D
А
Н
М
15
8
Ответ: длина основания ВС = 7
Задача №10
Тангенс острого угла прямоугольной трапеции равен Найдите её большее основание, если меньшее основание равно высоте и равно 4
В
С
4
tg D=
4
4
А
D
Н
DH = 4 : = 16, АD = 16 + 4 = 20
Ответ: большее основание равно 20
Задача №10
На стороне ВС прямоугольника АВCD, у которого АВ=12 и АD=17, отмечена точка Е так, что угол ЕАВ равен 45 0 . Найдите ЕD.
Рассмотрим АВЕ он прямоугольный и равнобедренный АВ = ВЕ = 12
Е
5
В
С
12
12
45 0
ЕС = ВС – ВЕ = 17 – 12 = 5
DE найдем по т. Пифагора
D
А
17
DE = 13
Ответ: DE = 13
Задача №10
Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба
Найдем стороны ромба.
Р = 4a а = 36:4 = 9
С
В
Проведем высоту
h
S = ah h= 27: 9= 3
А
D
Ответ: высота ромба равна 3.
Задача №11
1. Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
В ромбе диагонали точкой пересечения делятся пополам и пересекаются они под углом 90
50
40
Найдем половину второй диагонали по т.Пифагора
80
Половина второй диагонали равна 30, все диагональ 60.
S = 60 · 80 : 2 = 2400
Ответ: площадь ромба 2400
Задача №11
2. Площадь параллелограмма AВCD равна 6. Точка Е-середина стороны АВ. Найдите площадь трапеции ВCDЕ.
Опустим из вершины В высоту на сторону CD, эта высота общая и для параллелограмма и для трапеции
С
В
.
Е
D
А
= 4,5
Ответ: площадь трапеции равна 4,5
Задача №11
3. Периметр равнобедренного треугольника равен 216, а боковая сторона – 78. Найдите площадь треугольника
Найдем третью сторону
216 – 78 · 2 = 60
78
78
Проведем высоту к этой стороне, это и биссектриса и медиана
30
Найдем высоту h= 72
S м = 72 · 30 : 2 = 1080 S = 2· S м = 2160
Ответ: площадь треугольника равна 2160
Задачи для самостоятельного решения
- Основания равнобедренной трапеции равны 7 и 13, а ее боковые стороны равны 5. Найдите площадь трапеции .
- . Найдите площадь трапеции, изображённой на рисунке.
- Периметр квадрата равен 60. Найдите площадь квадрата
- Найдите площадь ромба, если его диагонали равны 14 и 6
- Высота равнобедренной (равнобокой) трапеции, проведенная из вершины С, делит основание AD на отрезки, длиной 1 и 5. Найдите длину основания ВС.
Задачи для самостоятельного решения
- Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба
- Найдите площадь квадрата, если его диагональ равна 20.
- . В трапеции АВСD АВ=CD, угол ВDА равен 10 0 и угол ВDС равен 109 0 Найдите угол АВD . Ответ дайте в градусах.
- Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Желаем удачи!
Мы верим в вас!
Вы справитесь!
ГАРЕЕВА
ДИНА СЕРГЕЕВНА
Получите свидетельство
Вход
Презентация по математике "Готовимся к ОГЭ. Модуль геометрия" (4.53 MB)
0
4556
874
Нравится
0
