Презентация по математике "Двугранный угол. Угол между плоскостями"

Используя презентацию учащиеся знакомятся с новым понятием "двугранный угол и его линейный угол", с алгоритмом построения линейного угла данного двугранного угла.

Отрабатывается навык  построения линейного угла через решение задач по готовым чертежам.

 Формируется конструктивный навык нахождения угла между плоскостями.

Прямая а разделяет плоскость на две полуплоскости.

а- общая граница полуплоскостей называется ребром двугранного угла.

Полуплоскости, образующие двугранный угол, называются его гранями.

Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не прилежащими одной плоскости.

Тема урока: Двугранный угол. Угол между плоскостями. Учитель: Клепикова Елена Ивановна МБОУ СОШ №6 г. Павлово, Нижегородской области

Цель урока:

• Ввести понятие двугранного угла и его линейного угла
• Рассмотреть задачи на применение этих понятий
• Сформировать конструктивный навык нахождения угла между плоскостями

• Прямая а разделяет плоскость на две полуплоскости

a

α

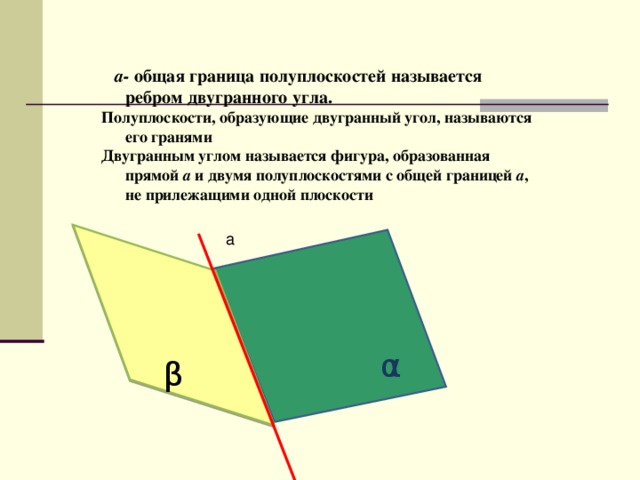
а- общая граница полуплоскостей называется ребром двугранного угла.

Полуплоскости, образующие двугранный угол, называются его гранями

Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а , не прилежащими одной плоскости

• а- общая граница полуплоскостей называется ребром двугранного угла. Полуплоскости, образующие двугранный угол, называются его гранями Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а , не прилежащими одной плоскости

β

α

Назовите предметы, имеющие форму двугранного угла

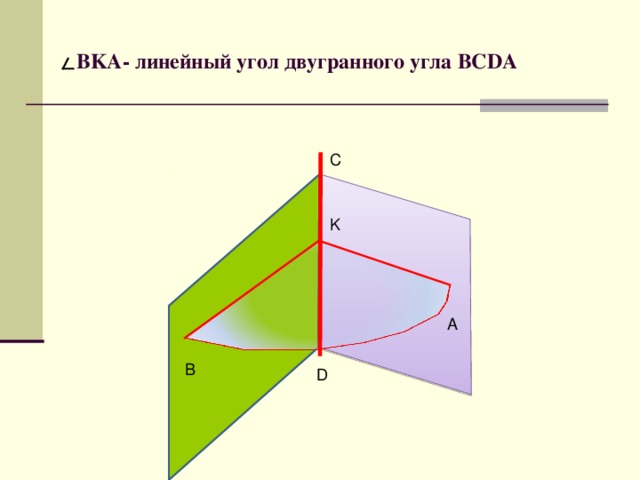
BKA- линейный угол двугранного угла BCDA

C

K

D

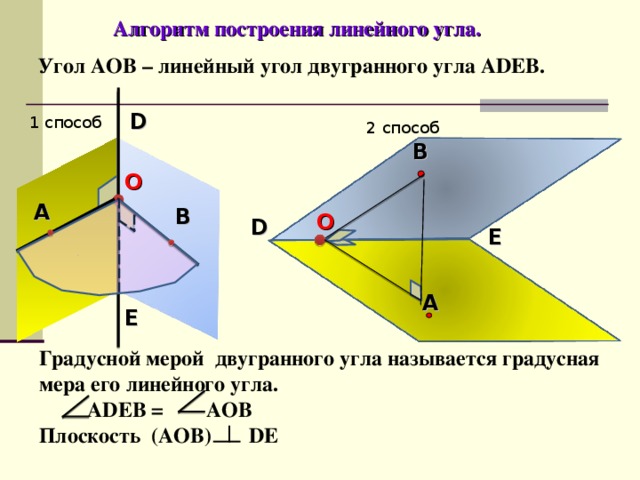
Алгоритм построения линейного угла.

Угол A О B – линейный угол двугранного угла ADEB .

D

1 способ

2 способ

B

O

A

B

O

D

E

A

E

Градусной мерой двугранного угла называется градусная мера его линейного угла.

ADEB = AOB

Плоскость (AOB) DE

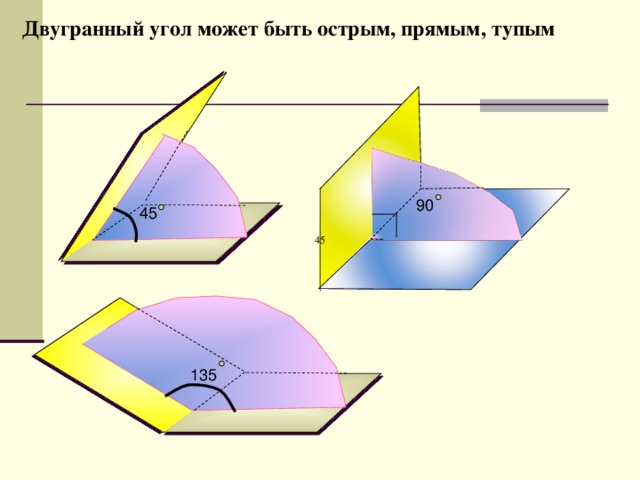
Двугранный угол может быть острым, прямым, тупым

90

45

135

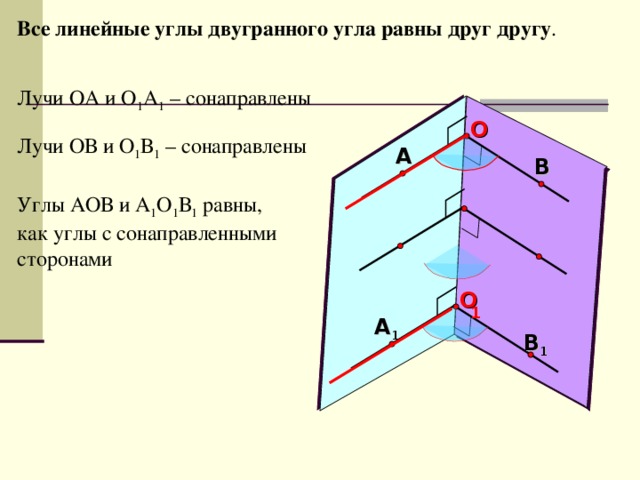
Все линейные углы двугранного угла равны друг другу .

Лучи ОА и О 1 А 1 – сонаправлены

O

Лучи ОВ и О 1 В 1 – сонаправлены

А

В

Углы АОВ и А 1 О 1 В 1 равны,

как углы с сонаправленными сторонами

O

1

А 1

В 1

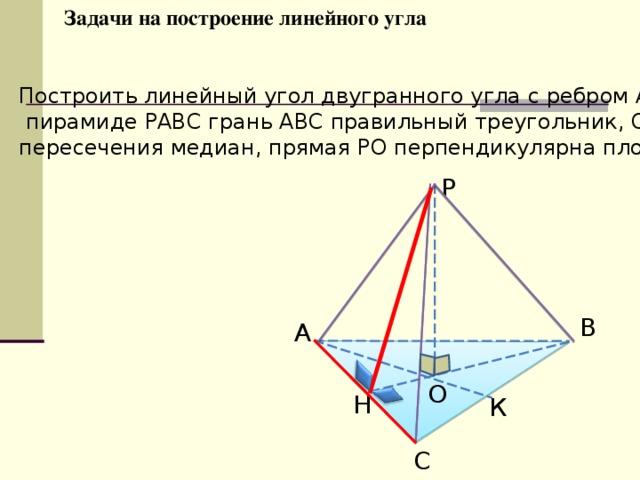
Задачи на построение линейного угла

Построить линейный угол двугранного угла с ребром АС, если в

пирамиде РАВС грань АВС правильный треугольник, О – точка

пересечения медиан, прямая РО перпендикулярна плоскости АВС.

Р

В

А

О

Н

К

С

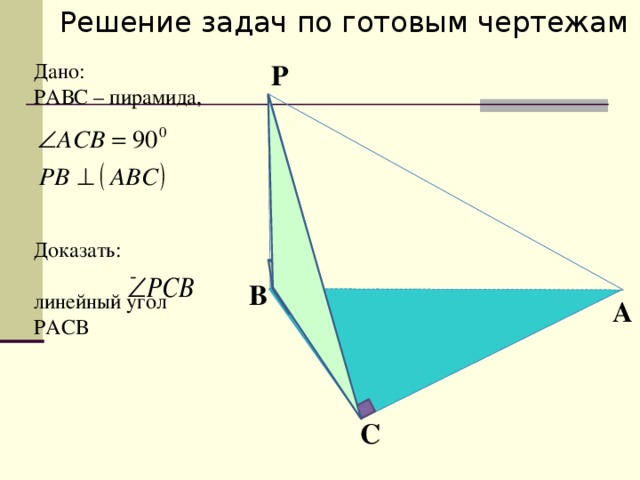
Решение задач по готовым чертежам

Р

Дано:

РАВС – пирамида,

Доказать:

- линейный угол РАСВ

В

A

С

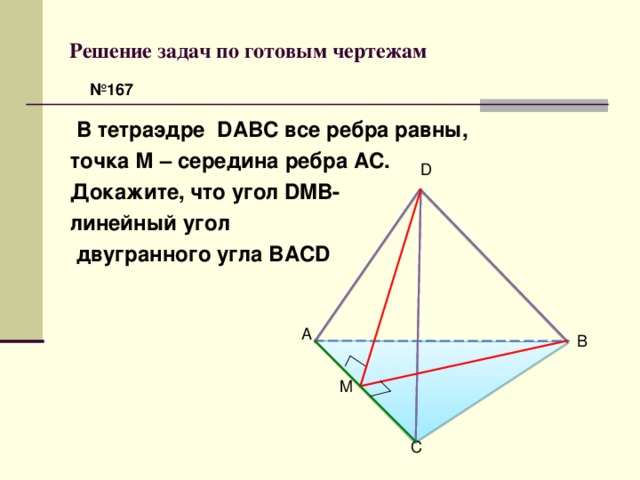
Решение задач по готовым чертежам

№ 167

В тетраэдре DABC все ребра равны,

точка М – середина ребра АС.

Докажите, что угол DMB-

линейный угол

двугранного угла BACD

D

A

B

M

C

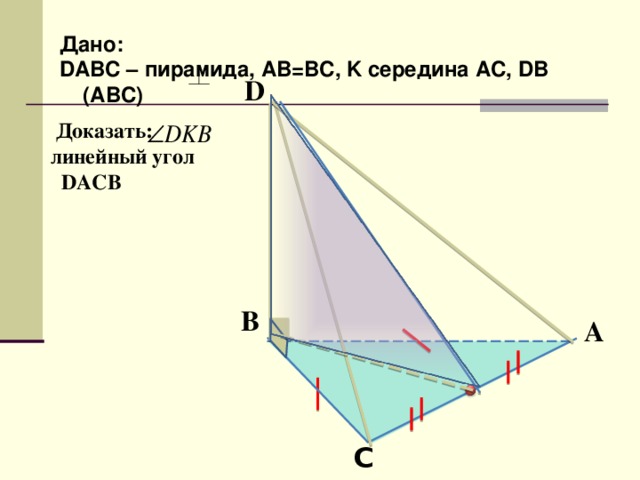
Дано:

D АВС – пирамида, AB=BC, K середина AC, DB (ABC)

Доказать:

линейный угол

DACB

D

В

А

K

С

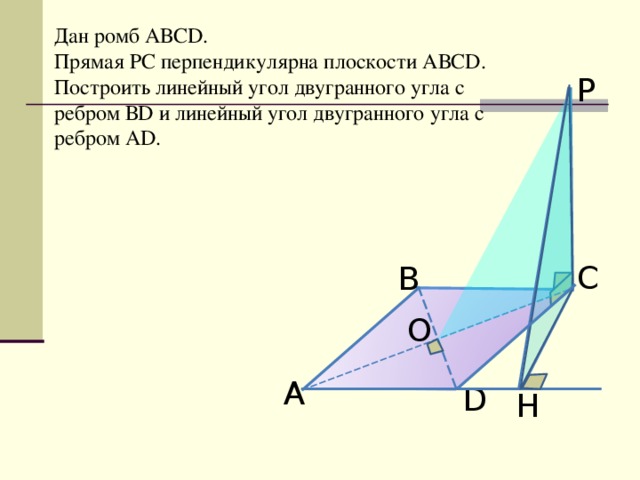
Дан ромб АВС D.

Прямая РС перпендикулярна плоскости АВС D.

Построить линейный угол двугранного угла с ребром В D и линейный угол двугранного угла с ребром А D .

P

С

В

O

А

D

H

В параллелограмме АВС D угол А D С равен , А D = 8 см,

D С= 6 см , прямая РС перпендикулярна плоскости ( АВС ) , РС= 9 см.

Найти величину двугранного угла с ребром А D и площадь

параллелограмма.

Решение:

P

120

H

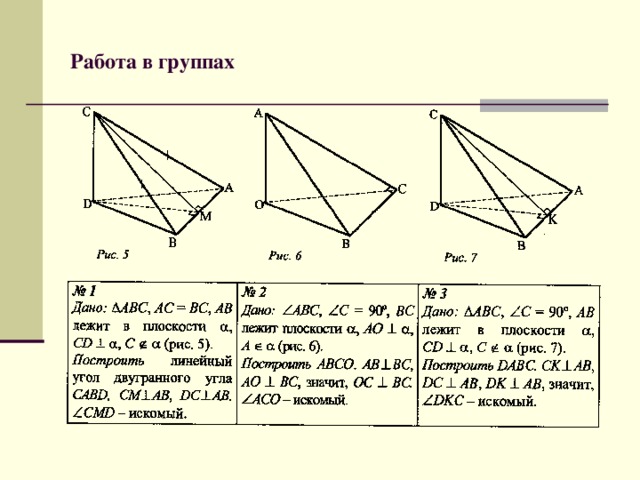
Работа в группах