
Доказательство неравенств
Презентация подготовлена
учителем математики МОУ Романовская СОШ
Атапиной Ириной Николаевной

«... Основные результаты математики
чаще выражаются неравенствами, а не равенствами».
Э. Беккенбах, Р. Беллман.

«Доказательства неравенств: использование равносильных преобразований, метода математической индукции, исследования функций. Неравенство о среднем геометрическом и среднем арифметическом нескольких чисел».

Задачи решение которых весьма затруднительно без применения классических неравенств, - частые гости на математических олимпиадах школьников. Решение задач такого типа обычно представляют собой последовательность достаточно простых рассуждений. Но вот логика и идеи всей цепочки этих элементарных звеньев – рассуждений выходят за рамки методов и приемов школьного курса. Тем более, что процесс доказательства неравенств неформален и мало алгоритмизуем.

Теоретические аспекты темы: «Доказательства неравенств»
Историческая справка.
Общие сведения о неравенствах.
Основные свойства неравенств.
Некоторые важные неравенства.
- Историческая справка. Общие сведения о неравенствах. Основные свойства неравенств. Некоторые важные неравенства.

Историческая справка.
- Понятия «больше» и «меньше» наряду с понятиями равенство возникли в связи со счетом предметов и необходимостью сравнивать различные величины.
 c/d (a,b,c,d положительные числа), то adcb » " width="640"
c/d (a,b,c,d положительные числа), то adcb » " width="640"
- Архимед ( III век до н.э.) указал границы числа π
- В трактате «Начала» Евклида, он доказывает, что среднее геометрическое двух положительных чисел не больше их среднего арифметического.
- В «Математическом собрании» Паппа Александрийского в III в. доказывается
- «Если a /bc/d (a,b,c,d положительные числа), то adcb »

- В 1557 году Роберт Рекорд впервые ввел знак равенства.
- В 1631 году английский ученый Гарриот ввел знаки неравенства.
- Французкий ученый П.Буге (1698-1758) ввел знаки ≤,≥

Одно из самых известных замечательных неравенств – это соотношение между средним арифметическим и средним геометрическим нескольких действительных неотрицательных чисел, опубликованное в1821 году французким математиком Огустеном Луи Коши. Ставшее столь популярным, что для него к настоящему времени найдены десятки доказательств и сотни применений.

Неравенство Коши Для любых неотрицательных чисел их среднее геометрическое не превосходит среднего арифметического. Равенство имеет место тогда и только тогда, когда все числа х 1 ,х 2 ,…,х n равны между собой .

- Неравенство Коши – Буняковского. Неравенство Чебышева. Неравенство Бернулли. Неравенство Иенсона.
- Неравенство Коши – Буняковского. Неравенство Чебышева. Неравенство Бернулли. Неравенство Иенсона.
- Неравенство Коши – Буняковского.
- Неравенство Чебышева.
- Неравенство Бернулли.
- Неравенство Иенсона.

Неравенство Коши – Буняковского Для любых действительных чисел х 1 ,х 2 ,…,х n и у 1 ,у 2 ,…,у n
 -1 и любого натурального числа n (1+x) n ≥ 1+nx " width="640"
-1 и любого натурального числа n (1+x) n ≥ 1+nx " width="640"
Неравенство Бернулли
Для любого х -1 и любого натурального числа n
(1+x) n ≥ 1+nx

Основные методы доказательства неравенств
2.1 Доказательство неравенств путем определения знака разности их частей
2.2 Доказательство неравенств с помощью использования ранее доказанных и очевидных неравенств
2.3 Метод оценивания
2.4 Доказательство неравенств методом от противного
2.5 Доказательство неравенств методом математической индукции
2.6 Метод использования тождеств
2.7 Метод ведения новых переменных (метод подстановки)
2.8 Метод интерпретации или моделей
2.9 Функционально – графические методы доказательства неравенств
2.10 Метод уменьшения числа переменных в неравенстве и понижения степени неравенства
- 2.4 Доказательство неравенств методом от противного 2.5 Доказательство неравенств методом математической индукции 2.6 Метод использования тождеств 2.7 Метод ведения новых переменных (метод подстановки) 2.8 Метод интерпретации или моделей 2.9 Функционально – графические методы доказательства неравенств 2.10 Метод уменьшения числа переменных в неравенстве и понижения степени неравенства
 0 выполняется неравенство (1+x) 1/3 Задача 2. (Вспомогательная.) При краткосрочных вкладах до востребования вклад S (например, рублей) увеличивается по следующему правилу: он растет ежедневно на р процентов от первоначальной суммы S (независимо от срока хранения). Найдите величину вклада спустя n дней его хранения в банке. " width="640"
0 выполняется неравенство (1+x) 1/3 Задача 2. (Вспомогательная.) При краткосрочных вкладах до востребования вклад S (например, рублей) увеличивается по следующему правилу: он растет ежедневно на р процентов от первоначальной суммы S (независимо от срока хранения). Найдите величину вклада спустя n дней его хранения в банке. " width="640"
Неравенства в финансовой математике
- Задача 1 . Доказать, что при х 0 выполняется неравенство (1+x) 1/3
- Задача 2. (Вспомогательная.) При краткосрочных вкладах до востребования вклад S (например, рублей) увеличивается по следующему правилу: он растет ежедневно на р процентов от первоначальной суммы S (независимо от срока хранения). Найдите величину вклада спустя n дней его хранения в банке.

- Задача3. (Вспомогательная.) Пусть увеличение так называемого срочного вклада S производится на р процентов через t месяцев хранения. Определите величину вклада S n спустя nt
( n - натуральное) месяцев хранения в банке, если договор продлевался (пролонгировался) после каждого из
t, 2t, 3t, ... , ( n - 1) t месяцев хранения.
 2) по договору начисляются p/n %. " width="640"
2) по договору начисляются p/n %. " width="640"
- Задача 4. Сравните возрастание через год вклада, положенного по договору под р % прибыли в год, и вклада той же первоначальной величины, если через каждые части года 1/n,2/n,… ,
( n-1 ) /n ( n натуральное, n 2) по договору начисляются p/n %.
![Метод оценивания в задачах ЕГЭ В9 Найдите наибольшее значение функции y = 19 – 2 cos x – 18 x / π на отрезке [-2 π /3; 0 ] .](https://fsd.videouroki.net/html/2014/03/26/98678908/img17.jpg)
Метод оценивания в задачах ЕГЭ
- В9 Найдите наибольшее значение функции y = 19 – 2 cos x – 18 x / π на отрезке [-2 π /3; 0 ] .
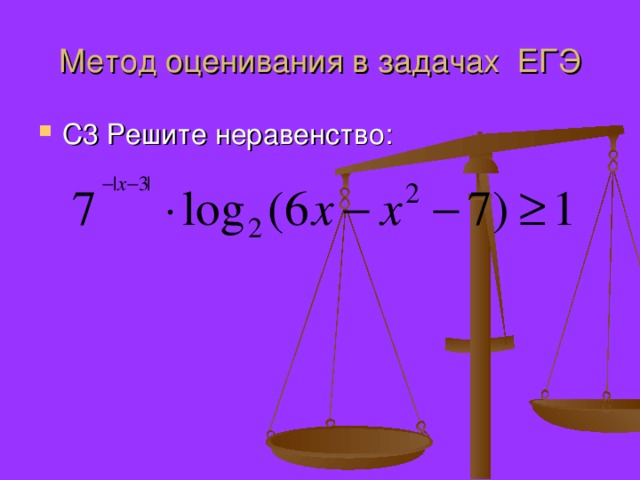
Метод оценивания в задачах ЕГЭ
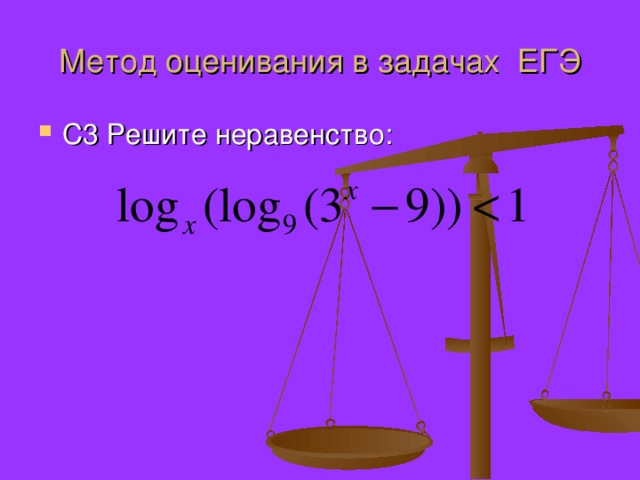
Метод оценивания в задачах ЕГЭ

Методические рекомендации по изучению темы: «Доказательства неравенств» в школьном курсе математики.
- Ю.Н. Макарычев «Алгебра – 8»,
- С.М. Никольский «Алгебра и начала анализа – 10»,
- А.Г.Мордкович, П.В. Семенов «Алгебра и начала анализа – 10»,
- А.Г.Мордкович, П.В. Семенов «Алгебра и начала анализа – 11»,
- Г.В. Дорофеев, Л.В. Кузнецова «Алгебра и начала анализа – 10»,
- Подготовка к ЕГЭ.

Введение в программу темы «Доказательства неравенств» направлено на устранение существующей в школьном курсе математики резкой диспропорции между решением неравенств и доказательством неравенств, и, что особенно важно, доказательство неравенств – один из важнейших видов математической деятельности, тогда как решение неравенств – «привилегия» именно школьной математики.

Таким образом, изучение темы: «Доказательства неравенств» на профильном уровне дает возможность реализовать такие задачи как формирование учащихся навыка осмысления и применение приемов доказательство неравенств; научить применять приемы доказательства неравенств при выполнении различных задач; уметь анализировать, обобщать и делать выводы; логически излагать мысли и творчески относится к делу.


 Получите свидетельство
Получите свидетельство Вход
Вход








 c/d (a,b,c,d положительные числа), то adcb » " width="640"
c/d (a,b,c,d положительные числа), то adcb » " width="640"





 -1 и любого натурального числа n (1+x) n ≥ 1+nx " width="640"
-1 и любого натурального числа n (1+x) n ≥ 1+nx " width="640"

 0 выполняется неравенство (1+x) 1/3 Задача 2. (Вспомогательная.) При краткосрочных вкладах до востребования вклад S (например, рублей) увеличивается по следующему правилу: он растет ежедневно на р процентов от первоначальной суммы S (независимо от срока хранения). Найдите величину вклада спустя n дней его хранения в банке. " width="640"
0 выполняется неравенство (1+x) 1/3 Задача 2. (Вспомогательная.) При краткосрочных вкладах до востребования вклад S (например, рублей) увеличивается по следующему правилу: он растет ежедневно на р процентов от первоначальной суммы S (независимо от срока хранения). Найдите величину вклада спустя n дней его хранения в банке. " width="640"

 2) по договору начисляются p/n %. " width="640"
2) по договору начисляются p/n %. " width="640"
![Метод оценивания в задачах ЕГЭ В9 Найдите наибольшее значение функции y = 19 – 2 cos x – 18 x / π на отрезке [-2 π /3; 0 ] .](https://fsd.videouroki.net/html/2014/03/26/98678908/img17.jpg)
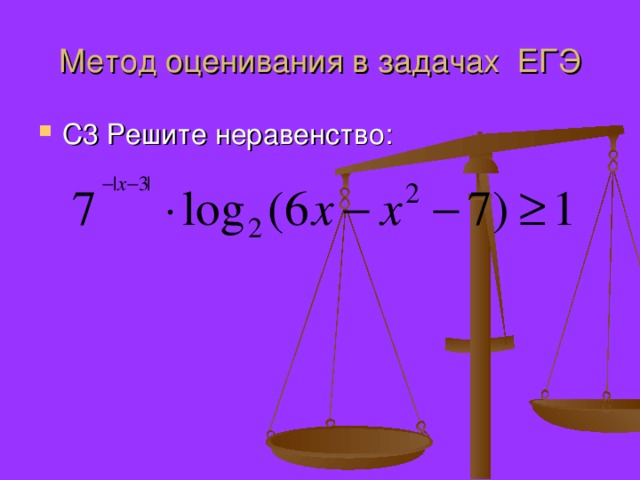
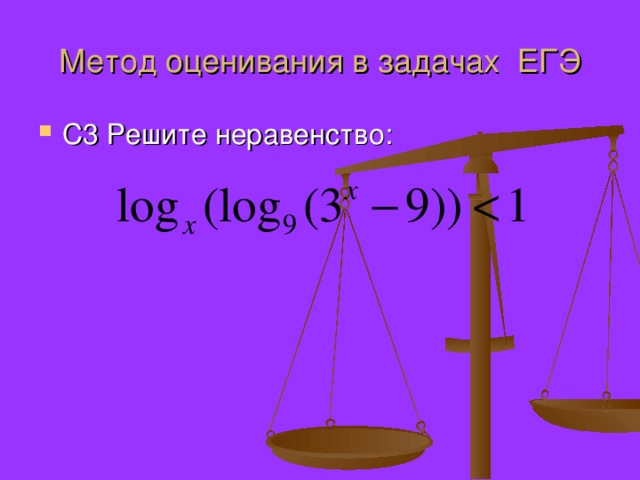












 Презентация по математике "Доказательство неравенств" (0.78 MB)
Презентация по математике "Доказательство неравенств" (0.78 MB)
 0
0 2216
2216 289
289 Нравится
0
Нравится
0




