4-ое измерение:
фантастика или реальность?
Работу выполнила:
Кузьменко Майя Андреевна
Что мы знаем о Вселенной? О том мире, в котором живём? И что такое пространство? Время? Материя и не материя? Это известные вопросы человечества! И чем больше мы понимаем, тем больше возникает вопросов.
Мы живем в 3-х мерном пространстве. На рубеже 19-го и 20-го веков швейцарский математик, физик и астроном Людвиг Шлефли выдвинул идею о том, что если наше физическое пространство имеет размерность 3, то ничто не может помешать нам представить себе пространство размерности 4,5 и даже большей размерности.
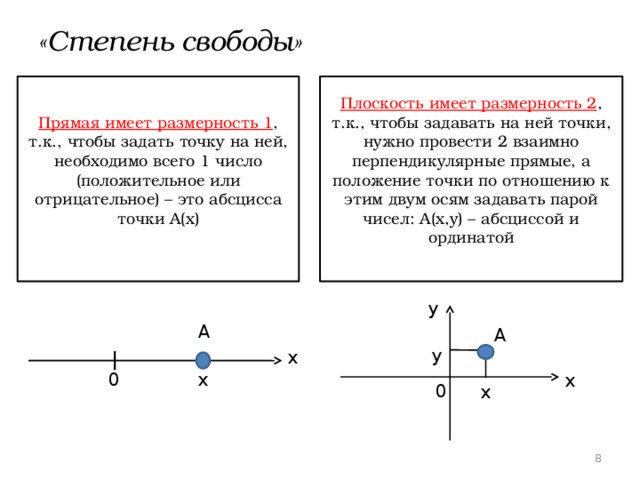
«Степень свободы»
Плоскость имеет размерность 2 , т.к., чтобы задавать на ней точки, нужно провести 2 взаимно перпендикулярные прямые, а положение точки по отношению к этим двум осям задавать парой чисел: А(х,у) – абсциссой и ординатой
Прямая имеет размерность 1 , т.к., чтобы задать точку на ней, необходимо всего 1 число (положительное или отрицательное) – это абсцисса точки А(х)
y
А
A
y
x
x
0
x
0
x
8
z
A
0
y
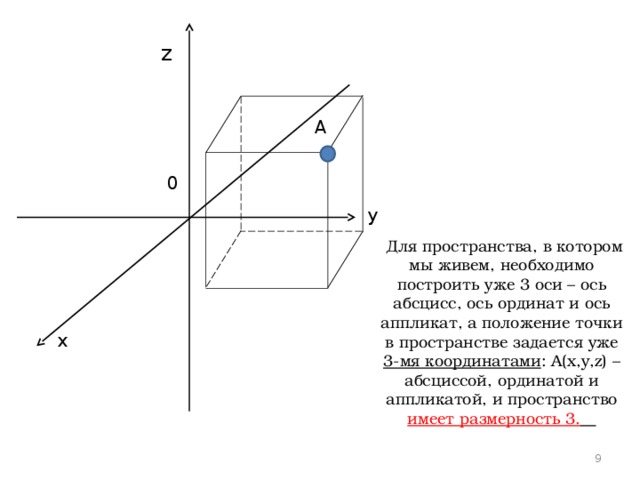
Для пространства, в котором мы живем, необходимо построить уже 3 оси – ось абсцисс, ось ординат и ось аппликат, а положение точки в пространстве задается уже 3-мя координатами : А(х,у,z) – абсциссой, ординатой и аппликатой, и пространство имеет размерность 3.
x
9
Конечно, хотелось бы продолжить,
но в пространстве невозможно провести
4-ю ось, перпендикулярно трём
предыдущим!
Это и не удивительно, т.к. пространство в котором мы живем, имеет размерность 3.
9
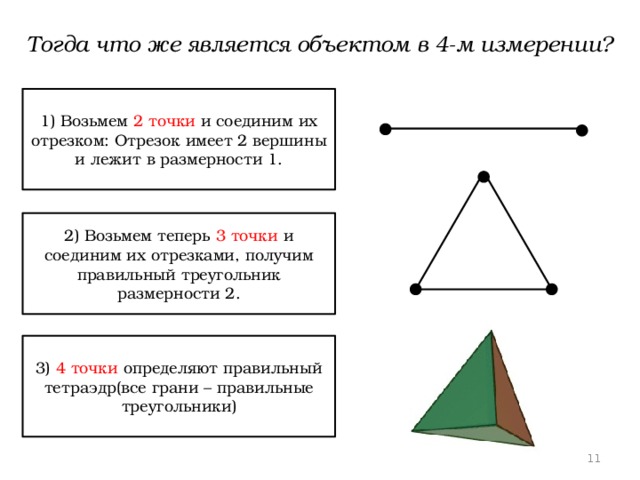
Тогда что же является объектом в 4-м измерении?
1) Возьмем 2 точки и соединим их отрезком: Отрезок имеет 2 вершины и лежит в размерности 1.
2) Возьмем теперь 3 точки и соединим их отрезками, получим правильный треугольник размерности 2.
3) 4 точки определяют правильный тетраэдр(все грани – правильные треугольники)
9
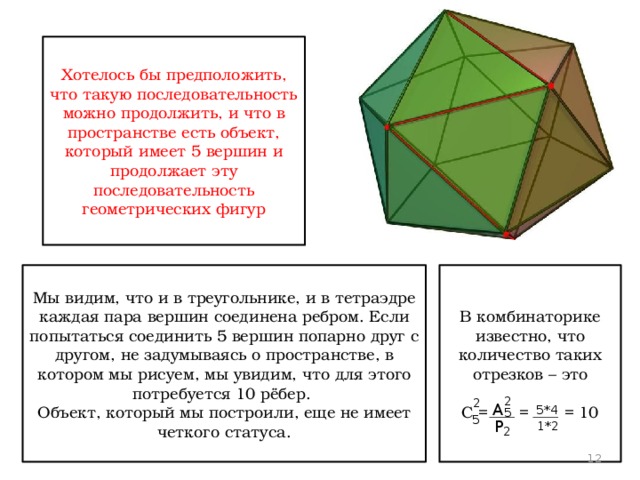
Хотелось бы предположить, что такую последовательность можно продолжить, и что в пространстве есть объект, который имеет 5 вершин и продолжает эту последовательность геометрических фигур
Мы видим, что и в треугольнике, и в тетраэдре каждая пара вершин соединена ребром. Если попытаться соединить 5 вершин попарно друг с другом, не задумываясь о пространстве, в котором мы рисуем, мы увидим, что для этого потребуется 10 рёбер.
В комбинаторике известно, что количество таких отрезков – это
Объект, который мы построили, еще не имеет четкого статуса.
С = = = 10
2
2
А
5*4
5
5
Р
1*2
2
12
Введем некоторые определения:
1. Точкой 4-х мерного пространства называется упорядоченная четверка чисел (x; y; z; u).
2. Координатными осями называются множества точек, одна из координат точек принимает любые числовые значения, а остальные равны 0.
Тогда в 4-х мерном координатном пространстве будут 4 координатные оси:
- Ось ОХ – множество точек вида (х; 0; 0; 0), где х – любое число
- Ось ОY – множество точек вида (0; y; 0; 0), где х – любое число
- Ось ОZ – множество точек вида (0; 0; z; 0), где х – любое число
- Ось ОU – множество точек вида (0; 0; 0; u), где х – любое число
12
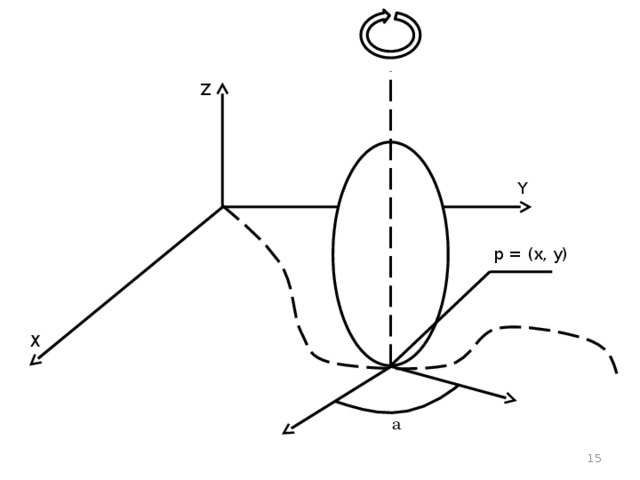
Рассмотрим пример
Нам нужны 4 координаты для описания положения колеса, которое без скольжения движется вперед по поверхности: 2 координаты для описания точки касания колеса с поверхностью, одна – для угла поворота, и еще одна – для угла вращения вокруг продольной оси. Это делает пространство положений колеса 4-х мерным.
Если мы добавим движение, то придётся ввести еще 4 координаты для скорости. Таким образом, пространство положений колеса, движущегося по поверхности, имеет 8 измерений.
12
Z
Y
p = (x, y)
X
a
15
Плоскость uz
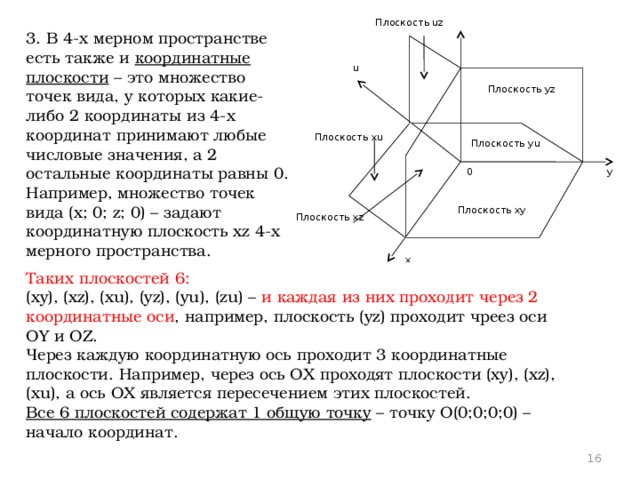
3. В 4-х мерном пространстве есть также и координатные плоскости – это множество точек вида, у которых какие-либо 2 координаты из 4-х координат принимают любые числовые значения, а 2 остальные координаты равны 0. Например, множество точек вида (x; 0; z; 0) – задают координатную плоскость xz 4-х мерного пространства.
u
Плоскость yz
Плоскость xu
Плоскость yu
y
0
Плоскость xy
Плоскость xz
x
Таких плоскостей 6:
(xy), (xz), (xu), (yz), (yu), (zu) – и каждая из них проходит через 2 координатные оси , например, плоскость (yz) проходит чреез оси OY и OZ.
Через каждую координатную ось проходит 3 координатные плоскости. Например, через ось OX проходят плоскости (xy), (xz), (xu), а ось ОХ является пересечением этих плоскостей.
Все 6 плоскостей содержат 1 общую точку – точку О(0;0;0;0) – начало координат.
16
Но в каком же смысле можно говорить о расстоянии между 2 точками в 4-х мерном пространстве? Мы знаем, что метод координат даёт возможность определять расстояние между точками, не опираясь на геометрические представления.
Действительно ,
а) на прямой: |AB|= |x 2 -x 1 | или |AB|= (x 2 -x 1 ) 2
б) на плоскости:|AB|= (x 2 -x 1 ) 2 + (y 2 -y 1 ) 2
в) в 3-х мерном пространстве:|AB|= (x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 + (z 2 -z 1 ) 2
Естественно предположить, что в 4-х мерном пространстве |AB| можно найти аналогично: |AB|= (x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 + (z 2 -z 1 ) 2 + (u 2 -u 1 ) 2 что соответствует определению расстояния между двумя точками A(x 1 ; y 1 ; z 1 ; u 1 ) и B(x 2 ; y 2 ; z 2 ; u 2 ) 4-х мерного пространства.
В частности, если т.В совпадает с точкой О(0;0;0;0), то
|AО|= x 2 + y 2 + z 2 + u 2
Пользуясь этим определением, можно решать задачи из геометрии 4-х мерного пространства
16
Вывод: треугольник АВС – прямоугольный; угол С = 90 0 16 " width="640"
Пример : Доказать, что треугольник АВС – прямоугольный, если А(4; 7; -3; 5); В(3; 0; -3; 1); С(1; 3; -2; 0).
Доказательство :
а) |АВ|= 1+49+0+16 = 66
б) |АС|= 9+16+1+25 = 51
в) |ВС|= 4+9+1+1 = 15
2) Сравним |AB| 2 и |AС| 2 + |ВС| 2 :
66 = 51+15 =
Вывод: треугольник АВС – прямоугольный; угол С = 90 0
16
0≤x≤1
0≤y≤1
0≤z≤1
0≤u≤1
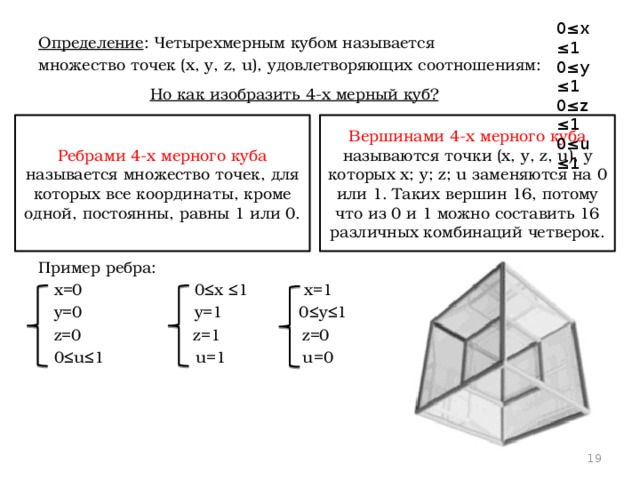
Определение : Четырехмерным кубом называется
множество точек (x, y, z, u), удовлетворяющих соотношениям:
Пример ребра:
x=0 0≤х ≤1 x=1
y=0 y=1 0≤y≤1
z=0 z=1 z=0
0≤u≤1 u=1 u=0
Но как изобразить 4-х мерный куб?
Вершинами 4-х мерного куба называются точки (x, y, z, u), у которых x; y; z; u заменяются на 0 или 1. Таких вершин 16, потому что из 0 и 1 можно составить 16 различных комбинаций четверок.
Ребрами 4-х мерного куба называется множество точек, для которых все координаты, кроме одной, постоянны, равны 1 или 0.
19
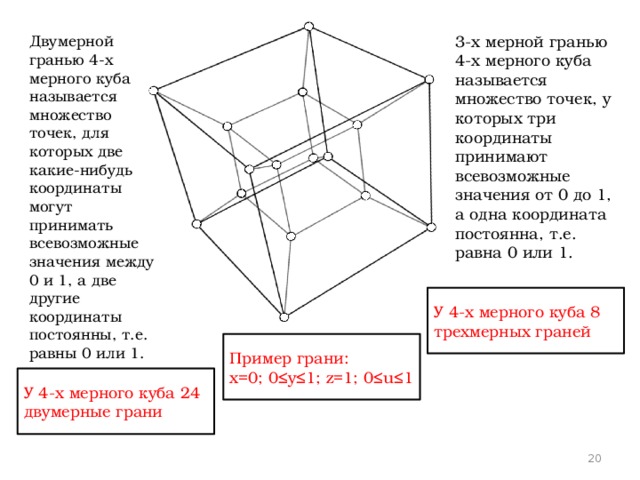
3-х мерной гранью 4-х мерного куба называется множество точек, у которых три координаты принимают всевозможные значения от 0 до 1, а одна координата постоянна, т.е. равна 0 или 1.
Двумерной гранью 4-х мерного куба называется множество точек, для которых две какие-нибудь координаты могут принимать всевозможные значения между 0 и 1, а две другие координаты постоянны, т.е. равны 0 или 1.
У 4-х мерного куба 8 трехмерных граней
Пример грани:
х=0; 0≤у≤1; z=1; 0≤u≤1
У 4-х мерного куба 24 двумерные грани
16
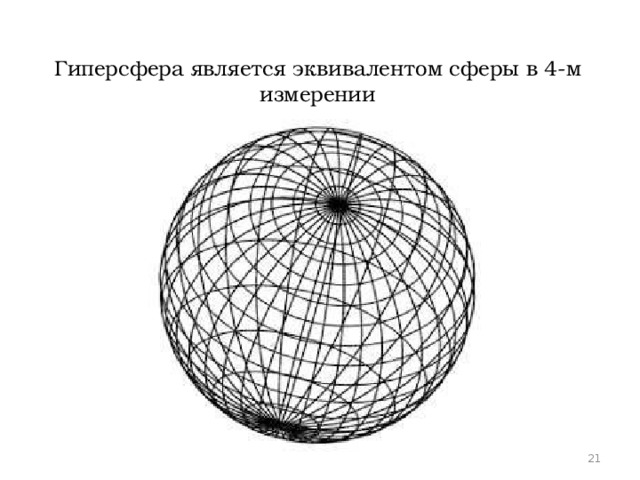
Гиперсфера является эквивалентом сферы в 4-м измерении
16
Есть теорема : Любые 4 отрезка, выходящие из одной точки, представляют взаимно – перпендикулярные оси 4-х мерного пространства.
Как вычислить объем четырехмерного шара?
а) Нужно найти гиперкуб, у которого был бы такой же объем.
б) Если объем гиперкуба равен α, то длина его ребра равна ⁴ α ; но вручную эту задачу решить практически невозможно. Но на языке js, встроенного в систему Вектор, это сделать можно.
Тогда, если R гипершара = 1, то объем гипершара = 4.934802200544679, а сторона гиперкуба = 1.49045008944290901
Гиперобъём 4-х мерного шара вычисляется по формуле:
П²R⁴ , где R – радиус гипершара
2
V⁴ =
16
Т.о. видно, что нет более банального утверждения, что окружающий нас мир представляет собой 4-х мерный пространственно-временной континумум.
16
x=0; y=0 – 1 решение n = 1: х² + у² ≤1 = (0;1);(0;-1);(1;0);(-1;0) – 4 решения n = 2: х² + у² ≤2 = (0;1);(0;-1);(1;0);(-1;0);(1;1);(-1;1);(1;-1);(-1;-1) – 9 реш . И т.д.: при n = 3 – тоже 9 решений при n = 4 – 13 решений при n = 5 – 21 решение при n = 10 – 37 решений при n = 50 – 161 решение при n = 100 – 317 решений 16 " width="640"
Герман Минковский
(1864-1909г.)
Минковский применил геометрические свойства 4-х мерного пространства для решения уравнений и неравенств в целых числах.
Рассмотрим неравенство х² + у² ≤ n ² . Выясним, сколько решений в целых числах оно имеет.
Рассмотрим решение неравенства для небольших значений n:
- n = 0: х² + у² ≤0 = x=0; y=0 – 1 решение
- n = 1: х² + у² ≤1 = (0;1);(0;-1);(1;0);(-1;0) – 4 решения
- n = 2: х² + у² ≤2 = (0;1);(0;-1);(1;0);(-1;0);(1;1);(-1;1);(1;-1);(-1;-1) – 9 реш .
- И т.д.: при n = 3 – тоже 9 решений
при n = 4 – 13 решений
при n = 5 – 21 решение
при n = 10 – 37 решений
при n = 50 – 161 решение
при n = 100 – 317 решений
16
N ≈ n , т.е. данное неравенство х² + у² ≤ n ² имеет столько решений в целых числах, сколько точек (x; y) с целыми координатами попадает в круг радиуса n. N n Аналогичные рассуждения Минковский провел для неравенства х² + у² + z² ≤ n ² , а для решения неравенства х² + у² + z² + u² ≤ n ² предложил ввести 4-х мерное пространство , и решения этого неравенства (x; y; z; u) предложил считать точкой 4-х мерного пространства . Тогда неравенство х² + у² + z² + u² ≤ n ² можно рассматривать как условие того, что точка (x; y; z; u) лежит внутри 4-х мерного шара радиуса n с центром в начале координат. 16 " width="640"
Мы видим, что число решений N растет с возрастанием n, но угадать точный закон изменения N трудно. Хотя, можно составить отношение N к n и мы увидим, что это отношение стремится к известному числу:
4.2; 3.7; 3.45; 3.22; 3.17;…. т.е. → = 3.14159265…
= N ≈ n , т.е. данное неравенство х² + у² ≤ n ² имеет столько решений в целых числах, сколько точек (x; y) с целыми координатами попадает в круг радиуса n.
N
n
Аналогичные рассуждения Минковский провел для неравенства х² + у² + z² ≤ n ² , а для решения неравенства
х² + у² + z² + u² ≤ n ² предложил ввести 4-х мерное пространство , и решения этого
неравенства (x; y; z; u) предложил считать точкой 4-х мерного пространства . Тогда неравенство х² + у² + z² + u² ≤ n ² можно рассматривать как условие того, что точка (x; y; z; u) лежит внутри 4-х мерного шара радиуса n с центром в начале координат.
16
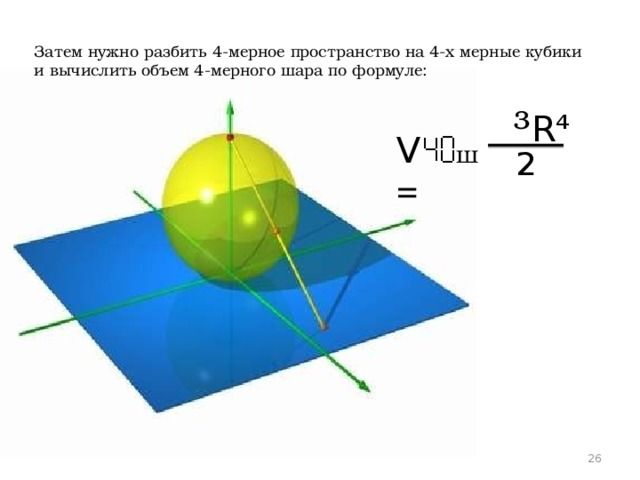
Затем нужно разбить 4-мерное пространство на 4-х мерные кубики и вычислить объем 4-мерного шара по формуле:
³
R⁴
V ш =
2
16
Идеи 4-х мерного пространства у ученых позаимствовали писатели-фантасты и художники. Герои их произведений, используя свойства 4-х мерного пространства , могли съесть содержимое яйца, не повредив скорлупу; выпить напиток, не разбивая бутылку; похитить сокровища из сейфа через 4-е измерение; хирурги выполняли операции, не разрезая ткани тела пациента.
16
«Порядок и хаос»
Звездный додекаэдр (двенадцатигранник), расположенный в центре, как мыльным пузырем, накрыт прозрачной сферой. В этом символе порядка и красоты отражается хаос в виде гетерогенного собрания ненужных, разбитых и сплющенных предметов.
16
Все картины Сальвадора Дали – это путешествие в мир 4-го измерения.
16
16
Тема 4-го измерения в литературе неразрывно связана с английским писателем Гербертом Уэллсом . В романе «Человек-невидимка» главный герой стал невидимым благодаря формуле, которая является геометрическим выражением, включающим 4 измерение.
16
Где еще говорится о 4-м измерении:
- «Алиса в Зазеркалье» (Льюис Керролл)
- «Остров доктора Моро» (Герберт Уэллс)
- «Прекрасные, но обреченные» (Френсис Скотт Фицджеральд)
- «Тайна» (Антон Чехов)
- «Мастер и Маргарита» (Михаил Булгаков)
- «В поисках утраченного времени (Марсель Пруст)
- «Путешествие в космос в поисках 4-го измерения» (Галина Зеленкина)
16
Века идут, года уходят,
Но все живущее – не сон!
Оно живет и превосходит
Вчерашней истины закон.
(Н. Заболоцкий)
16
Литература
- «Четвертое измерение» – Рауль Ибаньес
- «Метод координат» - библиотека физико-математической школы И.М. Гельфанда
- «4-ое измерение» - материалы из Интернета
16
Получите свидетельство
Вход
Презентация по математике "Четвёртое измерение: фантастика или реальность?" (9.41 MB)
0
2186
128
Нравится
0
