
Арифметическая и геометрическая прогрессии.
Подготовка к ЕНТ.
Учитель математики
высшей категории
Соколова В.А.
Цель: з акрепить знания по теме : “ Прогрессии ” .

Цели проведения консультации: .повторить основные определения, формулы, свойства арифметической и геометрической прогрессии; .повторить решение некоторых элементарных задач; .систематизировать знания учащихся; .рассмотреть примеры решений некоторых нестандартных задач; .расширить знания учащихся по теме «Арифметическая и геометрическая прогрессии»; .повысить интерес к математике; .подготовить учащихся к сдаче ЕНТ, выпускных экзаменов.

Закончился 20 век Куда стремится человек? Изучен космос и моря, Строенье звёзд и вся земля. Но математиков зовёт Известный лозунг «Прогрессия – движение вперёд.»
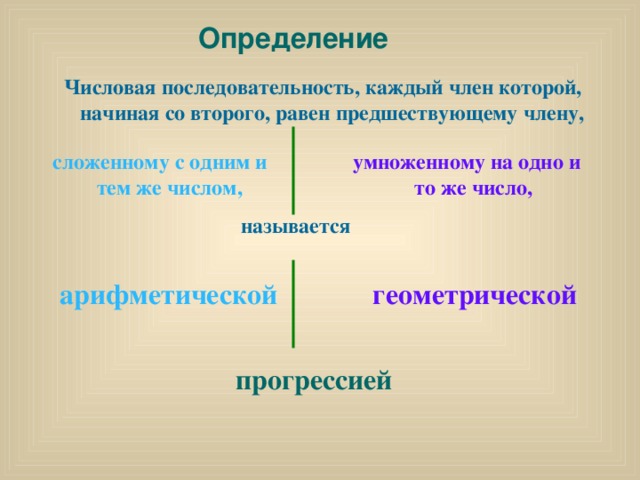
Определение
Числовая последовательность , каждый член которой , начиная со второго , равен предшествующему члену ,
сложенному с одним и тем же числом ,
умноженному на одно и то же число ,
называется
арифметической
геометрической
прогрессией

Формулы
1. Формулы n -ого члена арифметической прогрессии :
2. Сумма n первых членов арифметической прогрессии :
3. Формулы n -ого члена геометрической прогрессии :

4. Сумма n первых членов геометрической прогрессии :
5. Сумма бесконечно убывающей геометрической прогрессии :

Задание № 1
Является ли конечная последовательность...
Если данная последовательность является
то должны быть равны
второго и первого, третьего и второго, и т . д . членов : a 2 -a 1 =a 3 -a 2 =d b 2 :b 1 =b 3 :b 2 =q
10 ; 8 ,5; 7; 5,5
арифметической прогрессией ?
7; -1 4 ; 28 ; - 56
геометрической прогрессией ?
арифметической прогрессией ,
геометрической прогрессией ,
разности
частные

Задание № 2
Известно :
Найти :
Выразим из формулы n -го члена
арифметической прогрессии разность d :
Подставим :
геометрической прогрессии знаменатель q:
Подставим :
 a 11 =43 S 15 -S 14 =87,=a 15 =87 " width="640"
a 11 =43 S 15 -S 14 =87,=a 15 =87 " width="640"
Задание № 3
Дано: a 5 =19 a 14 =55
Найти: d=? Решение.
Задание № 4
Дано : S 11 -S 10 =43 S 15 -S 14 =87 Найти : d=? Решение.
S 11 -S 10 =43,=a 11 =43
S 15 -S 14 =87,=a 15 =87

Любой член арифметической прогрессии можно найти, как среднее арифметическое любых двух её членов и , равноотстоящих от .
Если , то

Задание № 5 Найти a 3 +a 9 , если a 6 =17. Решение.

Любой член геометрической прогрессии можно найти как среднее пропорциональное любых двух её членов и , равноотстоящих от .
Если , то
или

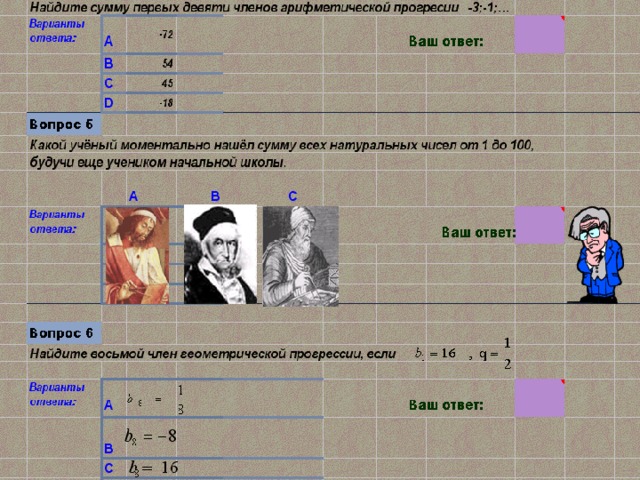
Задание № 6

Задание № 7













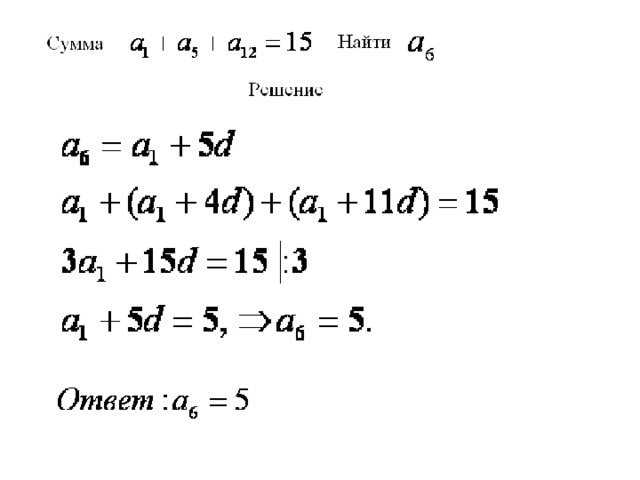






 Получите свидетельство
Получите свидетельство Вход
Вход











 a 11 =43 S 15 -S 14 =87,=a 15 =87 " width="640"
a 11 =43 S 15 -S 14 =87,=a 15 =87 " width="640"


















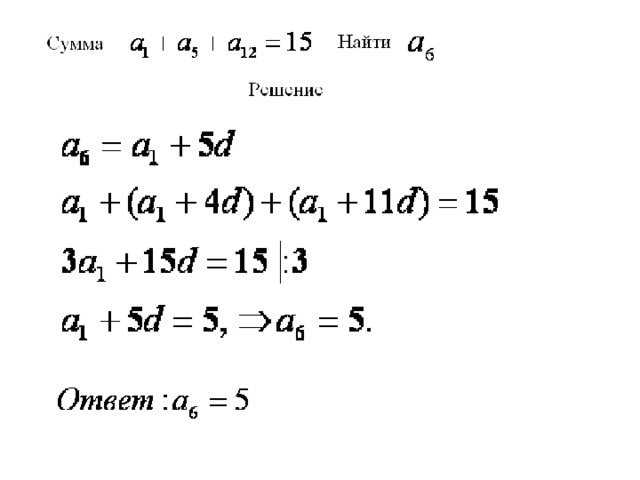















 Презентация по математике "Арифметическая и геометрическая прогрессии. Подготовка к ЕНТ" (2.03 MB)
Презентация по математике "Арифметическая и геометрическая прогрессии. Подготовка к ЕНТ" (2.03 MB)
 0
0 718
718 105
105 Нравится
0
Нравится
0


