Презентация по алгебре "Периодичность функций"

1. Найдите область определения функции:

1) [-2; 2];

2) [-3;1) ∪(1;4);

3) [-3;-2) ∪(-2; 4);

4) (-2; 2].

2. Укажите график нечётной функции:

3. Найдите область значений функции:

а) у = -4cos x.

1) [ -1; 1 ];

2) [ -4; 0 ];

3) [-4; 4];

4) (∞; ∞).

б) y = 3sin х/2

1) [-1,5; 1,5];

2) [ -3; 3];

3) (-3; 3);

4) [-1; 1].

Периодичность функций.

Мальцева М.И.

1. Найдите область определения функции:

y

3) [-3;-2) (-2; 4)

1) [-2; 2]

2

1

x

2) [-3;1) (1;4)

4) (-2; 2]

-3

4

-2

2. Укажите график нечётной функции:

у

у

у

у

х

х

х

х

1)

2)

3)

4)

2

3. Найдите область значений функции:

а) у = -4cos x

2) [ -4; 0 ]

3) [-4; 4]

4) (∞; ∞)

1) [ -1; 1 ]

б) y = 3sin х/2

3) (-3; 3)

4) [-1; 1]

2) [ -3; 3]

1) [-1,5; 1,5]

в) у =sin x - 2

3) [ -1; 1 ]

2) (-∞; ∞)

4) [ -3; 0]

1) [-3; -1]

г) y = sin 2 x + 3

2) [3;4]

3) [0;4]

4) [ 0; 3]

1) [0;1]

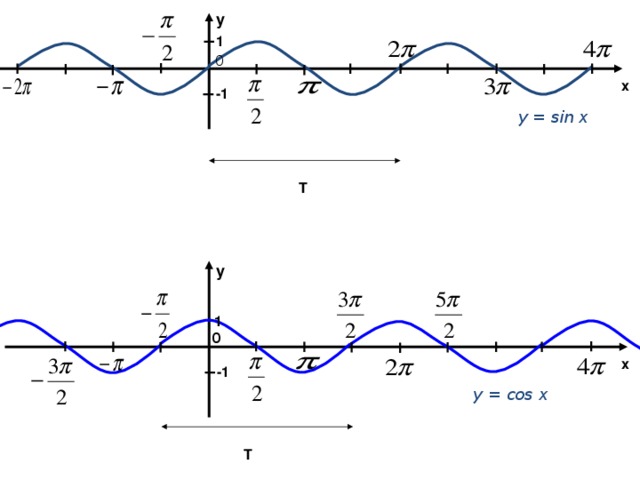
y

1

0

x

-1

у = sin x

T

y

1

0

x

-1

у = cos x

T

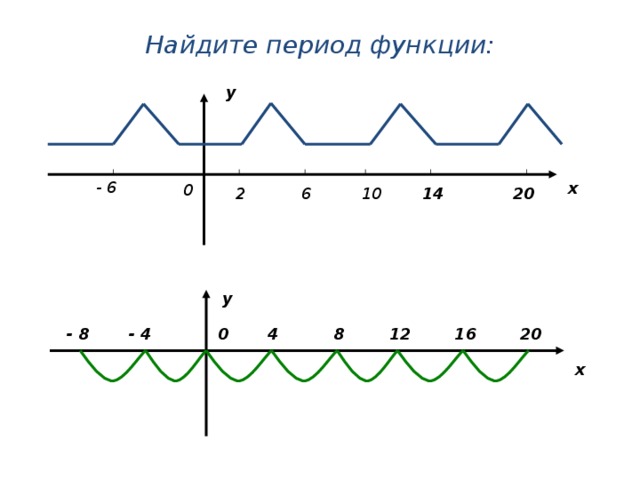
Найдите период функции:

y

- 6

x

0

20

14

10

6

2

y

4

8

- 8

- 4

20

16

12

0

x

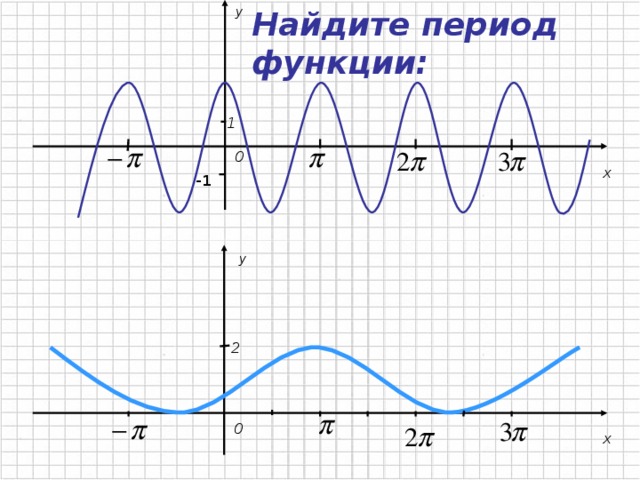
y

Найдите период функции:

1

0

x

-1

y

2

0

x

Достройте график функции

на промежутке [ -2T; 2,5 T].

y

0

x

3T/2

2,5T

-T/2

T/2

-2T

y

0

x

2,5T

-2T

-T/2

T/2

3T/2

Функция y=f(x) называется периодической , если существует такое число Т0, что для любого x из области определения этой функции выполняется равенство

f(x - T) = f(x) = f(x + T)

Число Т, удовлетворяющее указанному условию, называется периодом функции .

Если функция f периодическая и имеет период Т, то функция

Аf (k x + b),

где A, k и b постоянны,

а k ≠ 0, также периодична, причём её период равен

Найдите основной период функции:

а) у= sin 3x

Т = 2π/3

Т = 4π

б) у= cos 0,5 x

в) у= sin (-x/2 + π)

Т = 4π

Найдите наименьший положительный период функции:

а) у= sin 2x

Т = π

б) у= 3 cos (-0,75x)

Т = 8π/3

в) у= sin 4x/5

Т = 5π/2

Т = π

г) у= cos (2x + 2π/7)