Презентация "Квадрат Полибия"

Поли́бий (ок. 200 до н. э. — ок. 120 до н. э.) — древнегреческий историк, государственный деятель и военачальник, автор «Всеобщей истории» («Истории») в 40 томах, охватывающих события в Риме, Греции, Македонии, Малой Азии и в других регионах с 220 до н. э. по 146 до н. э. Полибий предложил шифр, ставший значительным шагом вперед, по сравнению с предыдущими системами шифрования.

Квадрат Полибия (Шахматная доска Полибия, Шифр Полибия, Тюремная азбука) - способ кодирования букв алфавита, с целью его приведения к виду, удобному для передачи по каналу связи. Данный вид кодирования изначально применялся для греческого алфавита, но затем был распространен на другие языки.

В Квадрате Полибия греческого алфавита буквы алфавита записывались в квадрат 5 на 5 (одна ячейка оставалась пустой), после чего с помощью оптического телеграфа передавались номер строки и столбца, соответствующие символу исходного текста (на каждую букву приходилось два сигнала: число факелов обозначало разряд буквы по горизонтали и вертикали).

Полную информацию смотрите в файле. 

Квадрат Полибия

Поли́бий (ок. 200 до н. э.— ок. 120 до н. э.) — древнегреческий историк, государственный деятель и военачальник, автор «Всеобщей истории» («Истории») в 40 томах, охватывающих события в Риме, Греции, Македонии, Малой Азии и в других регионах с 220 до н. э. по 146 до н. э. Полибий предложил шифр, ставший значительным шагом вперед, по сравнению с предыдущими системами шифрования.

Квадрат Полибия ( Шахматная доска Полибия, Шифр Полибия, Тюремная азбука ) - способ кодирования букв алфавита, с целью его приведения к виду, удобному для передачи по каналу связи. Данный вид кодирования изначально применялся для греческого алфавита, но затем был распространен на другие языки.

Квадрат Полибия в Древней Греции

В Квадрате Полибия греческого алфавита буквы алфавита записывались в квадрат 5 на 5 (одна ячейка оставалась пустой), после чего с помощью оптического телеграфа передавались номер строки и столбца, соответствующие символу исходного текста (на каждую букву приходилось два сигнала : число факелов обозначало разряд буквы по горизонтали и вертикали).

1

1

2

2

3

3

4

4

5

5

Квадрат Полибия с греческим алфавитом. Для передачи, например, буквы «Θ» сначала показывали два факела, потом три.

Тюремная азбука

Нередко Квадрат Полибия применялся, как средство передачи информации в тюрьме (через стенку), и поэтому получил название «Тюремная азбука» .

Первоначально редким стуком в стену камеры указывалась строка, а затем через краткую паузу частым стуком, отсчитывалась буква. Например , для того, чтобы выстукать слово «кто», нужно дважды стукнуть редко, а затем пять раз ударить часто (буква К), затем четыре раза стукнуть редко и три часто (буква Т) и, наконец, трижды ударить редко и четыре раза часто (О). Принимающий стуки записывает одну за другой передаваемые буквы и, таким образом, составляет целые слова и фразы.

1

1

А

2

2

3

Е

Б

3

В

Л

4

Ж

4

Г

З

5

5

М

Р

Х

Н

Д

С

И

6

О

Т

Ы

К

Ц

П

Ч

Ю

У

Ф

Я

Ш

Щ

-

-

Способ шифрования

Шаг 1: Формирование таблицы шифрования

К каждому языку отдельно составляется таблица шифрования с одинаковым (не обязательно) количеством пронумерованных строк и столбцов, параметры которой зависят от его мощности (количества букв в алфавите). Берутся два целых числа, произведение которых ближе всего к количеству букв в языке — получаем нужное число строк и столбцов. Затем вписываем в таблицу все буквы алфавита подряд — по одной на каждую клетку. При нехватке клеток можно вписать в одну две буквы (редко употребляющиеся или схожие по употреблению).

Число букв в русском алфавите отличается от числа букв в греческом алфавите, поэтому размер таблицы выбран другой (квадрат 6*6=36, поскольку 36 наиболее близкое число к 33):

Возможен также другой вариант составления, предусматривающий объединение букв Е и Ё, И и Й, Ъ и Ь. В данном случае получаем следующий результат:

1

1

2

2

А

Ж

3

3

Б

З

Н

В

4

4

И/Й

У

5

Г

О

5

Д

Щ

П

К

Ф

6

Х

Л

Ы

Е/Ё

Р

М

Ь/Ъ

С

Ц

Ч

Т

Э

Ю

Ш

Я

1

1

2

2

А

3

3

Б

Ё

В

4

4

Ж

Л

Г

5

М

С

З

5

Д

6

И

6

Н

Ч

Т

У

Е

О

Ш

Э

Й

Щ

Ф

К

П

Ю

Ъ

Я

Р

Х

Ы

-

Ц

Ь

-

-

Латинский алфавит

В современном латинском алфавите 26 букв, следовательно таблица должна состоять из 5 строк и 5 столбцов, так как 25=5*5 наиболее близкое к 26 число. При этом буквы I, J не различаются (J отождествляется с буквой I), так как не хватает 1 ячейки:

1

1

2

2

A

3

F

3

B

4

C

G

4

L

5

D

H

5

M

Q

I/J

N

E

R

V

W

S

K

O

T

X

P

Y

U

Z

Способ шифрования

Шаг 2: Принцип шифрования

Метод 1

Для шифрования на квадрате находили букву текста и вставляли в шифровку нижнюю от неё в том же столбце. Если буква была в нижней строке, то брали верхнюю из того же столбца. Зашифруем слово «SOMETEXT»:

Таблица координат

1

1

2

2

A

3

F

B

3

C

G

4

4

L

D

H

5

5

M

Q

I/J

E

N

R

V

W

S

K

O

T

X

P

Y

U

Z

Буква текста

S

Буква шифротекста

O

X

M

T

E

R

T

K

E

Y

X

K

C

Результат

До шифрования: SOMETEXT

После шифрования: XTRKYKCY

Метод 2

Сообщение преобразуется в координаты по квадрату Полибия, координаты записываются вертикально:

Таблица координат

Буква:

Координата вертикальная:

S

3

O

Координата горизонтальная:

4

M

4

2

E

3

3

5

T

4

E

1

4

5

X

3

1

5

1

1

2

A

2

3

F

B

3

4

4

C

G

L

5

D

H

5

M

Q

I/J

R

N

E

V

W

S

O

K

T

X

P

Y

U

Z

Затем координаты считывают по строкам:

34 25 45 34 43 31 41 54

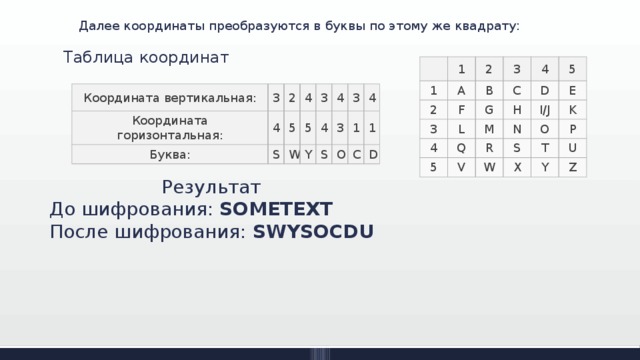
Далее координаты преобразуются в буквы по этому же квадрату:

Таблица координат

1

1

2

2

A

3

3

F

B

L

G

C

4

4

M

H

5

D

Q

5

N

I/J

E

R

V

O

K

W

S

P

X

T

Y

U

Z

Координата вертикальная:

3

Координата горизонтальная:

4

2

Буква:

S

5

4

5

3

W

4

Y

4

3

3

S

O

1

4

1

C

D

Результат

До шифрования: SOMETEXT

После шифрования: SWYSOCDU

Метод 3

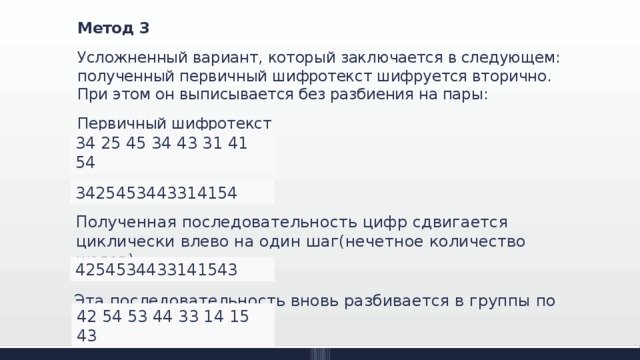
Усложненный вариант, который заключается в следующем: полученный первичный шифротекст шифруется вторично. При этом он выписывается без разбиения на пары:

Первичный шифротекст

34 25 45 34 43 31 41 54

3425453443314154

Полученная последовательность цифр сдвигается циклически влево на один шаг(нечетное количество шагов):

4254534433141543

Эта последовательность вновь разбивается в группы по два:

42 54 53 44 33 14 15 43

По таблице заменяется на окончательный шифротекст:

Таблица координат

1

1

2

2

A

3

3

F

B

L

G

C

4

4

M

H

5

D

Q

5

N

I/J

E

R

V

O

K

W

S

P

X

T

Y

U

Z

Координата вертикальная:

4

Координата горизонтальная:

2

5

Буква:

I

4

5

3

4

U

3

P

4

3

1

T

N

4

1

5

Q

V

Результат

До шифрования: SOMETEXT

После шифрования: IUPTNQVO

Добавление ключа

На первый взгляд шифр кажется очень нестойким, но для его реальной оценки следует учитывать два фактора:

• возможность заполнить квадрат Полибия буквами произвольно, а не только строго по алфавиту;
• возможность периодически заменять квадраты.

Тогда анализ предыдущих сообщений ничего не дает, так как к моменту раскрытия шифра он может быть заменен.

Буквы могут вписываться в таблицу в произвольном порядке — заполнение таблицы в этом случае и является ключом. Для латинского алфавита в первую клетку можно вписать одну из 25 букв, во вторую — одну из 24, в третью — одну из 23 и т. д. Получаем максимальное количество ключей для шифра на таблице латинского алфавита:

N=25*24*23*…*2*1=25!

Соответственно для дешифрования сообщения потребуется не только знание алфавита, но и ключа , с помощью которого составлялась таблица шифрования. Но произвольный порядок букв тяжело запомнить, поэтому пользователю шифра необходимо постоянно иметь при себе ключ — квадрат . Появляется опасность тайного ознакомления с ключом посторонних лиц. В качестве компромиссного решения был предложен ключ — пароль . Пароль выписывается без повторов букв в квадрат; в оставшиеся клетки в алфавитном порядке выписываются буквы алфавита, отсутствующие в пароле.

Зашифруем слово « SOMETEXT », используя ключ « DRAFT ». Составим предварительно таблицу шифрования с данным ключом, записывая символы ключа по порядку в таблицу, после них остальной алфавит:

1

1

D

2

2

3

R

B

3

I

A

4

4

C

O

F

5

E

5

K

V

L

T

P

G

M

H

Q

W

X

N

S

Y

U

Z

Преобразуем сообщение в координаты по квадрату Полибия:

Таблица координат

Буква:

S

Координата вертикальная:

O

Координата горизонтальная:

4

M

4

1

E

4

4

3

T

3

E

2

5

X

3

1

3

2

5

Считаем координаты по строкам:

41 43 53 35 44 32 12 51

Преобразуем координаты в буквы по этому же квадрату:

Таблица координат

Координата вертикальная:

Координата горизонтальная:

4

1

4

Буква:

F

3

5

3

3

M

4

5

N

4

3

X

1

2

S

2

E

B

1

1

D

2

2

3

R

B

3

A

I

4

4

C

5

O

K

E

F

5

L

T

V

P

G

H

W

M

Q

N

X

S

U

Y

Z

Результат

До шифрования: SOMETEXT

После шифрования: FMNXSEBT

Спасибо за внимание!