Презентация к уроку математики "Признаки равенства треугольников"

Цели и задачи:

1. Усвоение материала через практикум и теорию;

2. Формирование логического мышления;

3. Научиться видеть различие и сходство в доказательствах признаков;

4. Пытаться развивать способности обучающихся к самообразованию;

5. Формирование умений саморегулирования своей учебно-познавательной деятельности.

Практическая работа.

Построить треугольник по данной стороне и двум углам, прилежащим к ней.

Берем данный отрезок.

Откладываем угол 1.

Откладываем угол 2.

Продлим полупрямые, исходящие из углов 1 и 2.

Решение задач.

Дано: AB пересекает CD в точке О.

СО=ОD, АО=ОВ.

Доказать: тр-к АОD=тр-ку ВОС.

Дано: тр-к КМN = тр-ку SPR

периметр тр-ка KMN = 72 см.

PS = 20 см., SR = 25 см.

Найти: стороны тр-ка KMN.

ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ

7 класс

Рушева Т.Б.

Учитель математики,

МБОУ Алтунинская ООШ

ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ

1.Цели и задачи занятия

2.Практическая работа

3.Таблица признаков равенства треугольников

4.Решение задач

ЦЕЛИ И ЗАДАЧИ

1. Усвоение материала через практикум и теорию;

2. Формирование логического мышления;

3. Научиться видеть различие и сходство в доказательствах признаков;

4. Пытаться развивать способности обучающихся к самообразованию;

5. Формирование умений саморегулирования своей учебно- познавательной деятельности.

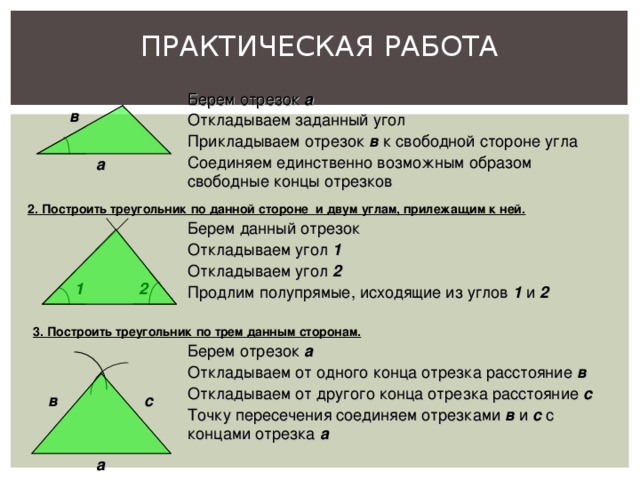
ПРАКТИЧЕСКАЯ РАБОТА

1. Построить треугольник по двум данным сторонам и углу между ними.

Берем отрезок а

в

Откладываем заданный угол

Прикладываем отрезок в к свободной стороне угла

Соединяем единственно возможным образом

свободные концы отрезков

а

2. Построить треугольник по данной стороне и двум углам, прилежащим к ней.

Берем данный отрезок

Откладываем угол 1

Откладываем угол 2

1

2

Продлим полупрямые, исходящие из углов 1 и 2

3. Построить треугольник по трем данным сторонам.

Берем отрезок а

Откладываем от одного конца отрезка расстояние в

Откладываем от другого конца отрезка расстояние с

в

с

Точку пересечения соединяем отрезками в и с с концами отрезка а

а

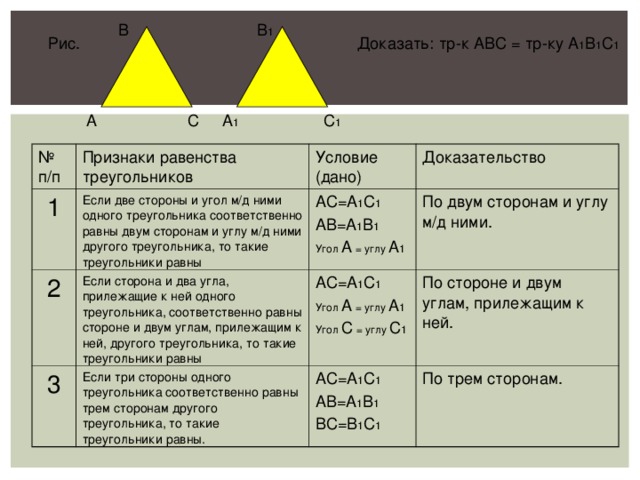
В 1

В

Доказать: тр-к АВС = тр-ку А 1 В 1 С 1

Рис.

С 1

А 1

С

А

№ п/п

Признаки равенства треугольников

1

Если две стороны и угол м/д ними одного треугольника соответственно равны двум сторонам и углу м/д ними другого треугольника, то такие треугольники равны

2

Условие (дано)

3

Если сторона и два угла, прилежащие к ней одного треугольника, соответственно равны стороне и двум углам, прилежащим к ней, другого треугольника, то такие треугольники равны

АС=А 1 С 1

АВ=А 1 В 1

Угол А = углу А 1

Доказательство

По двум сторонам и углу м/д ними.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

АС=А 1 С 1

Угол А = углу А 1

Угол С = углу С 1

По стороне и двум углам, прилежащим к ней.

АС=А 1 С 1

АВ=А 1 В 1

ВС=В 1 С 1

По трем сторонам.

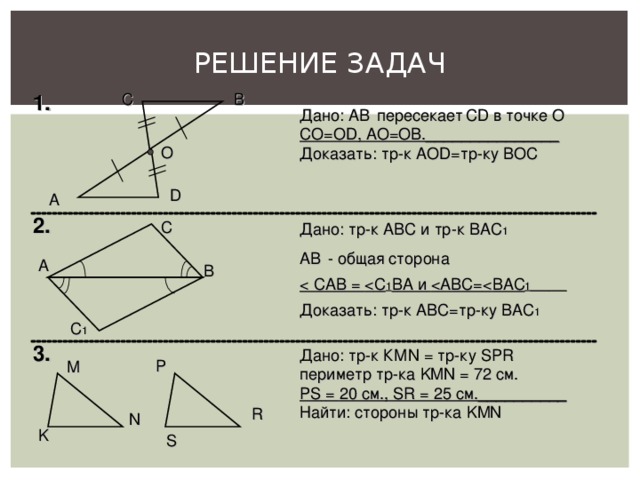
РЕШЕНИЕ ЗАДАЧ

С

В

1.

Дано: AB пересекает CD в точке О

СО=О D , АО=ОВ._______________

Доказать: тр - к АО D= тр-ку ВОС

О

D

А

2.

С

Дано: тр-к АВС и тр-к ВАС 1

AB - общая сторона

САВ = С 1 ВА и АВС= ВАС 1 ______

Доказать: тр - к АВС = тр-ку ВАС 1

А

В

С 1

3.

Дано: тр-к КМ N = тр-ку SPR

периметр тр-ка KMN = 72 см.

PS = 20 см., SR = 25 см.__________

Найти: стороны тр-ка KMN

P

М

R

N

K

S

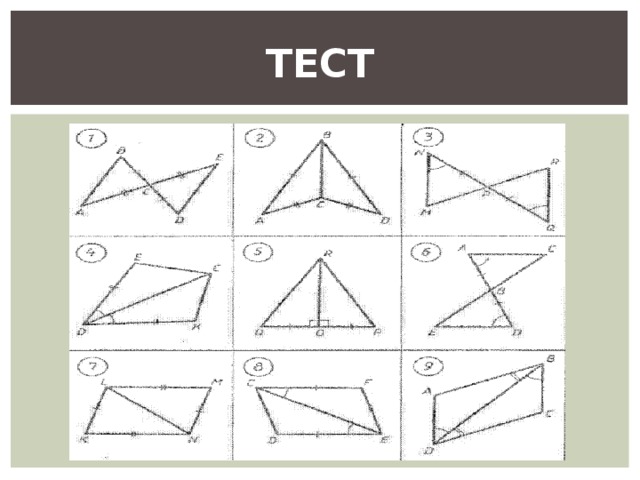
ТЕСТ

• Голова неподвижна. Движутся только глаза. В вытянутой руке карандаш. Движение карандаша: влево- вправо- вверх-вниз (3раза)
• Круговые движения глазами в одном, а затем в другом направлении - (6 - 7 раза)
• Нарисуйте глазами треугольники: маленький, средний, большой.

ИСТОРИЧЕСКИЙ ЭКСКУРС

Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – значит пережить приключение В. Произволов

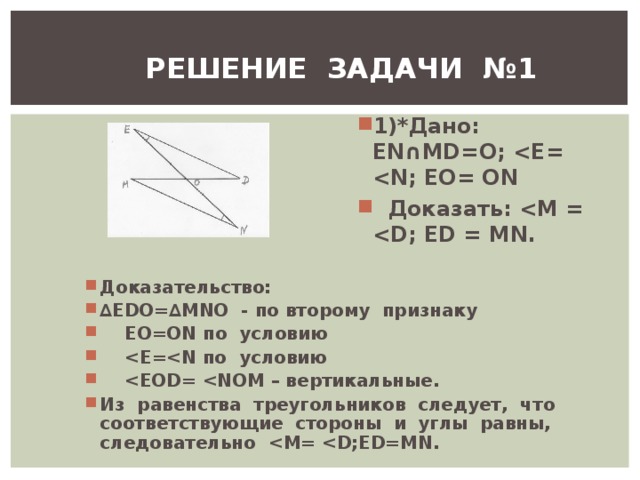
РЕШЕНИЕ ЗАДАЧИ №1

• 1)*Дано: Е N ∩ MD = O ; E = N ; ЕО= О N
• Доказать: M = D ; ED = MN .

• Доказательство:
• ∆ EDO =∆ MNO - по второму признаку
• EO = ON по условию
• E = N по условию
• EOD = NOM – вертикальные.
• Из равенства треугольников следует, что соответствующие стороны и углы равны, следовательно M = D ; ED = MN .

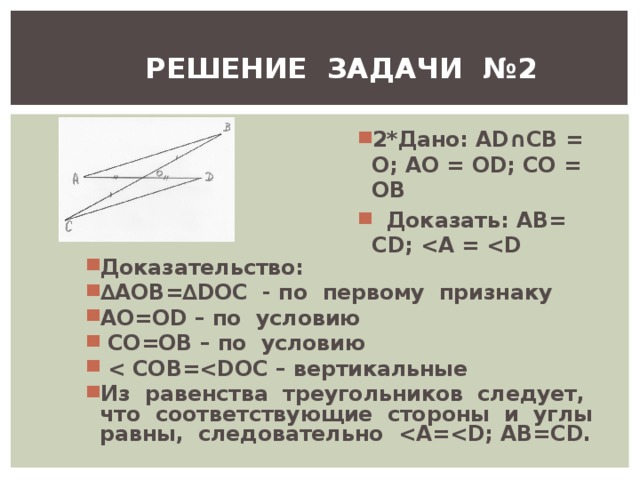
РЕШЕНИЕ ЗАДАЧИ №2

• 2*Дано: А D ∩СВ = О; АО = О D ; СО = ОВ
• Доказать: АВ= С D ; A = D

• Доказательство:
• ∆ AOB =∆ DOC - по первому признаку
• AO = OD – по условию
• CO =ОВ – по условию
• COB = DOC – вертикальные
• Из равенства треугольников следует, что соответствующие стороны и углы равны, следовательно A = D ; AB = CD .

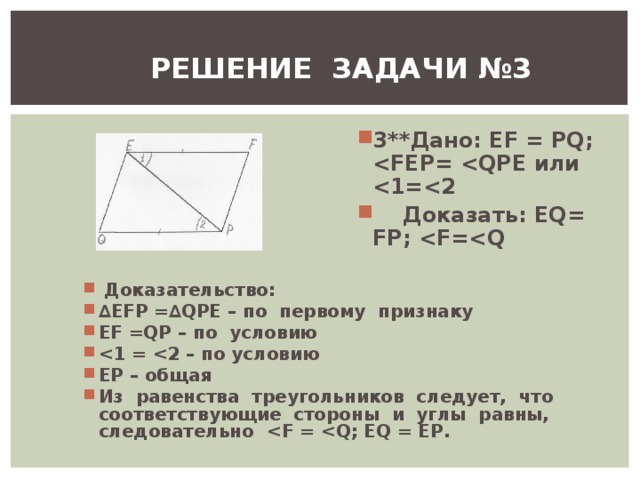
РЕШЕНИЕ ЗАДАЧИ №3

• 3** Дано : EF = PQ; Е или
• Доказать: Е Q = FP ; F = Q

• Доказательство:
• ∆ EFP =∆ QPE – по первому признаку
• EF = QP – по условию
• ЕР – общая
• Из равенства треугольников следует, что соответствующие стороны и углы равны, следовательно F = Q ; EQ = EP .

РЕШЕНИЕ ЗАДАЧИ №4

• ** Дано : ΔМ N Т и Δ MST; MN= MS; или

Доказать: NT = TS ; N = S

• Доказательство:
• ∆ MNT =∆ MST – по первому признаку
• MN = MS – по условию
• МТ – общая
• Из равенства треугольников следует, что соответствующие стороны и углы равны, следовательно N = S ; NT = TS .

Спасибо за урок