Презентация к уроку математики "Преобразование тригонометрических выражений. Разбор заданий из открытого банка заданий ЕГЭ"

Учиться можно только весело…

Чтобы переваривать знания, надо поглощать их с аппетитом.

Цель занятия:

Выработать навыки решения заданий на нахождение значений тригонометрических выражений, выделив общую идею решения.

Обеспечить применение этих навыков на практике.

Томас Пейн - англо-американский писатель, философ, публицист, прозванный «крёстным отцом США». В своей книге «Век Разума» (1794) назвал тригонометрию «душой науки».

Что используется в ходе решения данных выражений:

формулы приведения;

свойства периодичности тригонометрических функций;

свойство чётности нечётности;

основное тригонометрическое тождество;

формулы – синуса и косинуса двойного аргумента.

Учиться можно только весело….

Чтобы переваривать знания, надо поглощать их с аппетитом.

« Нахождение значений тригонометрических выражений »

Разбор заданий из открытого банка заданий  ЕГЭ по математике

Учитель математики МБОУ «СОШ № 34», г.Кемерово

Головина И.А.

Цель занятия:

• Выработать навыки решения заданий на нахождение значений тригонометрических выражений, выделив общую идею решения
• Обеспечить применение этих навыков на практике

Томас Пейн - англо- американский  писатель ,  философ ,  публицист , прозванный « крёстным отцом США ».  в своей книге « Век Разума » (1794) назвал тригонометрию «душой науки»

Что используется в ходе решения данных выражений:

формулы приведения

свойства периодичности тригонометрических функций

свойство чётности нечётности

формулы – синуса и косинуса двойного аргумента

основное тригонометри-

ческое тождество

Рекомендации:

если в выражении видите, что один угол больше другого в два раза, то смело используйте соответствующую тригонометрическую формулу двойного аргумента

если вы видите, что сумма данных углов (или их разность) составляет 90, 180, 270, 360 градусов, то применяйте формулы приведения

Найдите значение выражения :

2) Её периодичность, период равен 2 П , (360), cos(360*2+210)

• Свойство четности функции косинуса

cos(-t)=cost

3) И формулу приведения для косинуса

cos(180+30) = - cos30=

= - √3/2

4) -4√3* (- √3/2)= 6

Найдите значение выражения :

• Её периодичность, период равен П , (180),

tg(180*2+120)

• Свойство нечетности функции тангенса

tg(-t)=-tgt

3) И формулу приведения для косинуса

tg(90+30) = - ctg30=

= - √3

4) -44√3* (- √3)=132

Найдите значение выражения :

• Её периодичность, период равен 2 П , (360),

sin(360*2+60)

• Свойство нечетности функции синуса

sin(-t)=-sint

3) sin 60 = √3/2

4√3* √3/2=6

Найдите значение выражения :

Проверка:

1)

1) -5, tg(90+64),tg(180+64)

2)18

2)

3)-22

3)

4)33, cos(90-27)

4)

5)-34, sin(360-260)

5)

6)-38, cos(180-27)

6)

Найдите значение выражения :

Проверка:

1)

1) -40, sin 19=sin(90-71)

2)-7, sin270

2)

3)37, sin(180-7),sin(270-7)

3)

4) 22, tg(180-32)

4)

5) -20, sin(360+13)

5)

Решите самостоятельно :

1)

6)

2)

7)

3)

8)

9)

4)

10)

5)

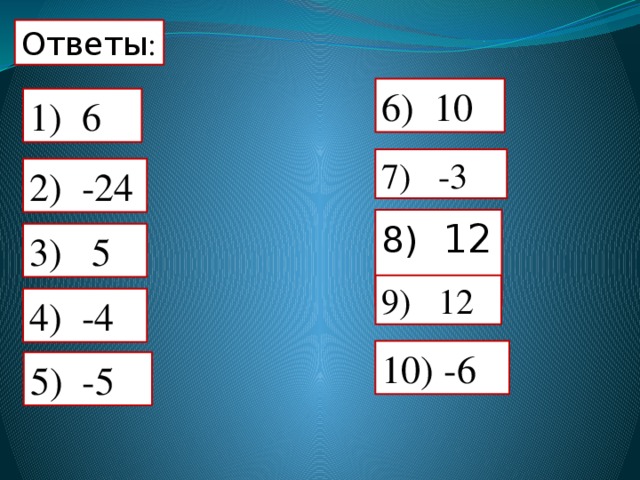
Ответы :

6) 10

1) 6

7) -3

2) -24

8) 12

3) 5

9) 12

4) -4

10) -6

5) -5

Домашнее задание:

Варианты 1-20

Задание № 10

До новых встреч !