Презентация к уроку математики на тему: "Введение декартовых координат в пространстве"

Презентация создана в помощь учителям математики для объяснения новой темы, а также школьникам (для самостоятельного изучения материала).

В ней представлен теоретический материал по теме "Введение декартовых координат в пространстве ".

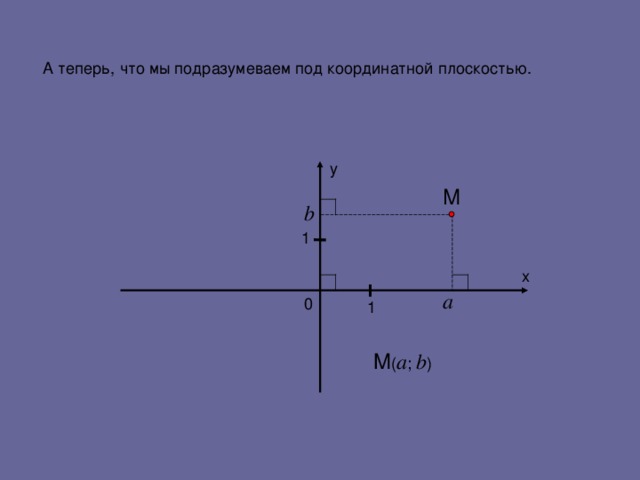
Цель данного урока: повторить применение координат на прямой и на плоскости; формулы середины отрезка и расстояния между точками.

Ввести  декартовы координаты в пространстве. Познакомить учащихся с формулами середины отрезка и расстояния между двумя точками в пространстве.

Развивать пространственное и логическое мышление. Прививать интерес к истории математики.

Воспитывать эстетический вкус и культуру оформления работы.

С помощью графиков и наглядных примеров учащимся легче будет освоить этот материал, закрепить и систематизировать знания по этой теме.

На уроке используются  задания  для работы по вариантам и у доски.

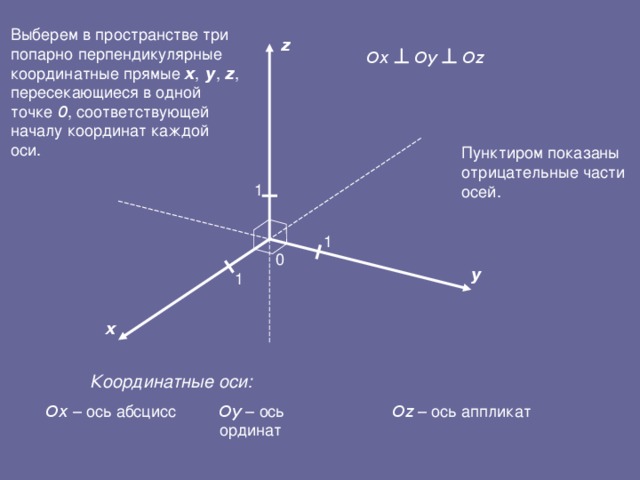
Выберем в пространстве три попарно перпендикулярные координатные прямые x, y, z, пересекающиеся в одной точке 0, соответствующей началу координат каждой оси.

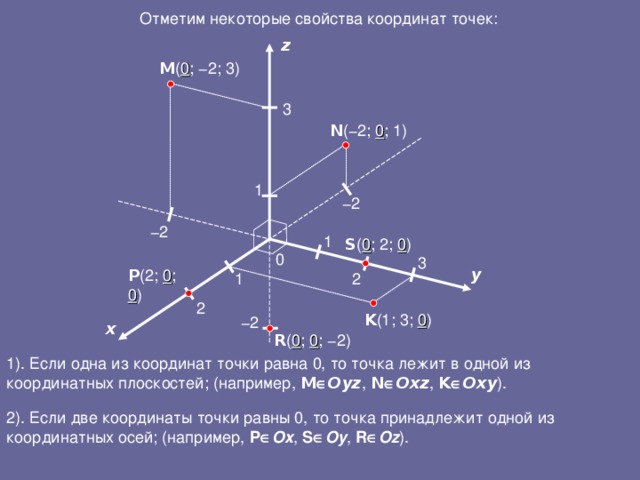
Отметим некоторые свойства координат точек:

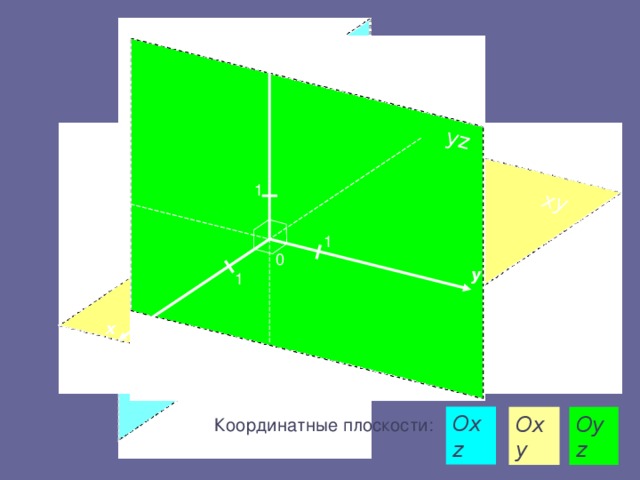
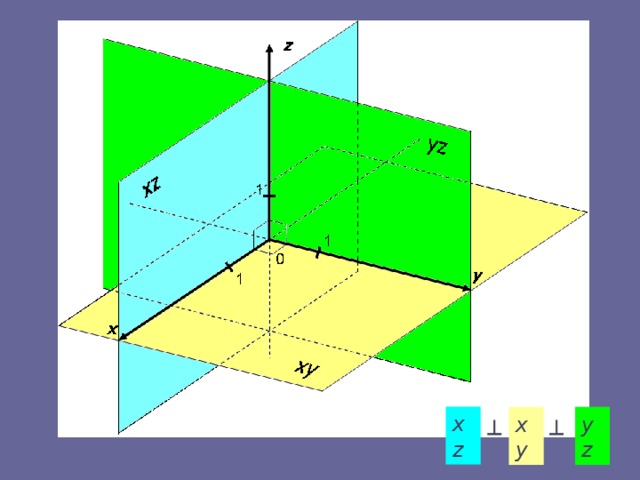
1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей;

2). Если две координаты точки равны 0, то точка принадлежит одной из координатных осей.

Введение декартовых координат в пространстве.

Формулы середины отрезка и расстояния между двумя точками.

Вспомним, как определяется координатная(числовая) прямая.

• Изображаем произвольную прямую;

2) Придаем ей положительное направление и обозначаем её;

3) Выбираем произвольную точку за начало отсчета;

4) Определяем длину единичного отрезка (масштаб).

М

х

0

1

а

Тогда любой точки этой координатной прямой соответствует единственное действительное число a . И наоборот, любое действительное число может быть изображено единственной соответствующей точкой, для которой это число является координатой. Записывают: M( a ).

А теперь, что мы подразумеваем под координатной плоскостью.

у

М

b

1

х

а

0

1

M ( a ; b )

Выберем в пространстве три попарно перпендикулярные координатные прямые x , y , z , пересекающиеся в одной точке 0 , соответствующей началу координат каждой оси.

z

Ox  Oy  Oz

Пунктиром показаны отрицательные части осей.

1

1

0

y

1

x

Координатные оси:

Oy – ось ординат

Ox – ось абсцисс

Oz – ось аппликат

xz

xy

yz

z

1

1

0

y

1

x

Oxz

Oxy

Oyz

Координатные плоскости:

xz

xy

yz

Координатные плоскости:





Отметим некоторые свойства координат точек:

z

M ( 0 ; − 2; 3)

3

N ( − 2; 0 ; 1)

1

− 2

− 2

1

S ( 0 ; 2; 0 )

0

3

y

P (2; 0 ; 0 )

2

1

2

K (1; 3; 0 )

− 2

x

R ( 0 ; 0 ; −2 )

1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей; (например, M  Oyz , N  Oxz , K  Oxy ).

2). Если две координаты точки равны 0, то точка принадлежит одной из координатных осей; (например, P  Ox , S  Oy , R  Oz ).

Формулы середины отрезка и расстояния между точками на плоскости.

Задача №1. Найдите координаты середины отрезка АВ и длину отрезка АВ, если:

1 вариант А (3;-1), В (-2;4)

2 вариант А (3;4), В (2; -1)

о

I вариант

Дано: А (3;-1), В (-2;4),

точка М – середина АВ.

Найти: IАВI, М(x;y) .

Решение:

Ответ:

II вариант

Дано: А (3;4), В (2;-1),

точка С – середина АВ.

Найти: IАВI, С(x;y).

Решение:

Ответ:

Расстояние между точками A(x 1 ; y 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 )

Координаты середины отрезка АВ, где A(x 1 ; y 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 )

Задача № 2.

Дано: А (1;-1;2), В (3;1;-2)

Найдите координаты середины отрезка АВ и его длину.

Спасибо за урок!