Презентация к уроку математики на тему "Однородные тригонометрические уравнения"

Области применения тригонометрических вычислений.

Триангуляция;

Акустика;

УЗИ;

Томография;

Геодезия;

Криптография.

№1. Вычислите и отгадайте, что по латыни означает слово «синус»?

1) arc tg 1

2) arc tg (- (3)^1/2)

3) arc tg 0

4) tg (arc cos ½)

5) tg (arc ctg  (3)^1/2 )

№2. Проверьте правильность решения уравнений.

Проверка домашнего задания.

№ 3.

1. 2sin²x – 7sinx + 3 = 0

2. 3sinx cos4x – cos4x = 0

3. 2 sinx -3 cosx = 0

4. 3 sin²x-4 sinx cosx+cos²x = 0

1. 2sin²x – 7sinx + 3 = 0

Пусть  sinx = t ,  тогда:

2t² – 7t + 3 = 0

Однородные тригонометрические уравнения

2

3

Области применения тригонометрических вычислений

• Триангуляция;
• Акустика;
• УЗИ;
• Томография;
• Геодезия;
• Криптография.

4

№ 1. Вычислите и отгадайте, что по латыни означает слово «синус»?

Б

И

З

-

Т

Г

0

С

2π

И

5

1

2

1) arc tg 1

2) arc tg (- )

3) arc tg 0

4) tg (arc cos ½)

5) tg (arc ctg )

3

4

5

№ 2. Проверьте правильность решения уравнений

π/3

х=±π/6 +2π n

х=π/3 +π n

х=1+π n

х=±π/6 + π n

х=(-1) n arcsin 1/3 + 2 πn

х= ± π/6 +2π n

х=±1/2 +2π n .

1) cos x = ½,

2) sin х = /2,

3) tg x = π /4,

4) с os x = /2,

5) sin x = 1/3,

6) cos x = - / 2,

7) cos x = π /3,

(-1) n

1 π /4

2π n

π n

5/6 π

1/2 π /3

6

Проверка домашнего задания

№ 3.

7

1. 2 sin ² x – 7 sinx + 3 = 0

1. 2 sin ² x – 7 sinx + 3 = 0

2. 3 sinx cos 4 x – cos 4 x = 0

3 . 2 sinx -3 cosx = 0

4 . 3 sin²x-4 sinx cosx + cos²x = 0

Пусть sinx = t , тогда:

2 t ² – 7 t + 3 = 0

2. 3 sinx cos 4 x – cos 4 x = 0

cos 4 x ( 3 sinx – 1) = 0

cos 4 x =0 или 3 sin x-1=0

8

3 . 2 sinx -3 cosx = 0

4 . 3 sin²x-4 sinx cosx + cos²x = 0

Определение .  Уравнение вида asinx + bcosx =0, где а≠0, b ≠0 называется однородным тригонометрическим уравнением первой степени.

Определение . 

Уравнение вида

asin ² x + bsinx cosx + ccos ² x =0 , где а≠0, b ≠0, с≠0 называется тригонометрическим уравнением второй степени.

9

Найдите лишнее уравнение:

1) sin x = 2 cos x ;

2) 2 sin x + 3 cos x = 0 ;

3) 3 sin x + 5 cos x = 0 ;

4) 2 sin x + cos x = 2 ;

5) sin²x - 2 sinx cosx + 4 cos²x = 0 .

10

2.

1.

х= arctg 7+ πn

х= arctg 3+ π n

х = - π /6 +πn

х= arctg (1/5)+ π n

х=- π/4 +π n

х= 1/2 arctg 5+π/2 n

х=π/8+π/2 n

4.

3.

Франсуа Виет (1540-1603)

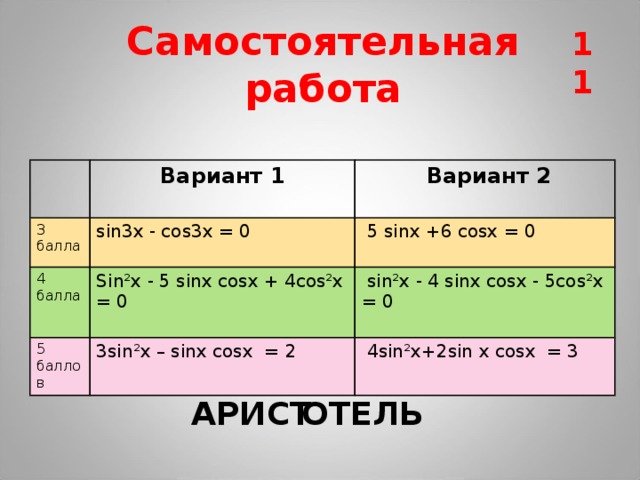
Самостоятельная работа

11

Вариант 1

3 балла

sin3x - cos3x = 0

4 балла

Вариант 2

Sin²x - 5 sinx cosx + 4cos²x = 0

5 sinx +6 cosx = 0

5 баллов

3sin²x – sinx cosx = 2

sin²x - 4 sinx cosx - 5cos²x = 0

4sin²x+2sin x cosx = 3

АРИСТ

ОТЕЛЬ

12

2

Задание на дом:

§ 7.17. Составить и решить

2 однородных уравнения

первой степени и

1 однородное уравнение

второй степени.

СПАСИБО ЗА УРОК !

Коллегам – за внимание!