Презентация к уроку математики "Математическое лото. Перпендикуляр и наклонная"

Цели урока:

1. рассмотреть возможные случаи взаимного расположения прямых в пространстве; формировать навык чтения и построения чертежей.

2. развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание.

3. воспитывать у учащихся ответственное отношение к учебному труду, волевые качества; формировать эмоциональную культуру и культуру общения.

Какие виды расположения прямых вы знаете? 

Перечислите.

Перпендикулярными называются две прямые, при пересечении которых образуется четыре прямых угла.

Задания:

1. Привести пример перпендикулярных прямых.

2. В треугольнике АВС угол А – прямой. Установите перпендикулярны ли прямые:

1) АВ и АС;

2) АВ и ВС;

3) АС и ВС.

Задача (письменно)

Лучи ОА, ОВ, ОС попарно перпендикулярны. Найдите периметр треугольника АВС, если ОА = ОВ = ОС = 5 см.

Сделайте рисунок.

Знания способны весь мир перевернуть

Там, где есть желание, всегда найдётся путь!!!

Цели урока:

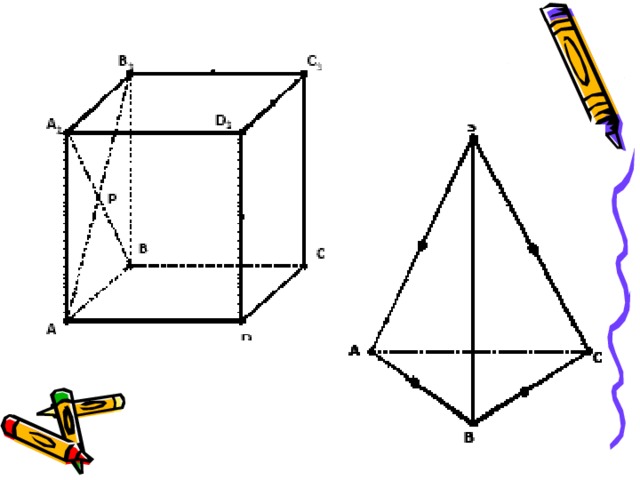
• рассмотреть возможные случаи взаимного расположения прямых в пространстве ; формировать навык чтения и построения чертежей.
• развивать пространственное воображение учащихся при решении геометрических задач , геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание.
• воспитывать у учащихся ответственное отношение к учебному труду, волевые качества; формировать эмоциональную культуру и культуру общения.

Какие виды расположения прямых вы знаете? Перечислите.

N

F

D

M

А

P

E

В

T

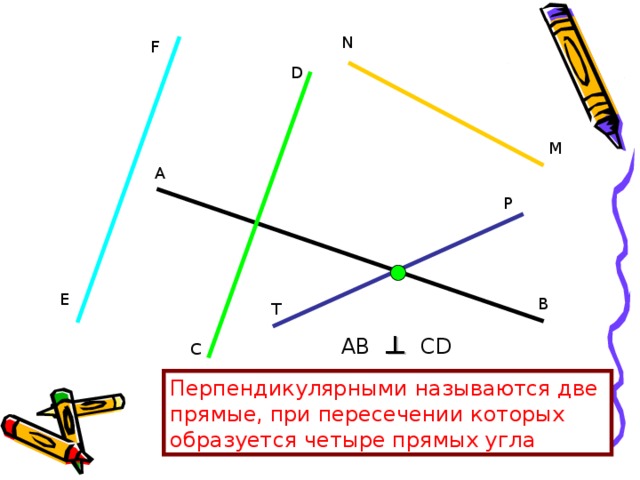
AB ⊥ CD

С

Перпендикулярными называются две

прямые, при пересечении которых

образуется четыре прямых угла

α

Задания:

• Привести пример перпендикулярных прямых.
• В треугольнике АВС угол А – прямой. Установите перпендикулярны ли прямые:

1) АВ и АС;

2) АВ и ВС;

3)АС и ВС.

Задача (письменно)

Лучи ОА, ОВ, ОС попарно перпендикулярны. Найдите периметр треугольника АВС, если ОА = ОВ = ОС = 5 см.

Сделайте рисунок.

Математическое лото

ТЕМА: «ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ»

1

2

4

3

5

6

1. Из точки вне плоскости проведены две наклонные, одна из которых равна 16 см и наклонена под углом 30 0 к плоскости. Определите длину второй наклонной, если её проекция на плоскость равна 6 см.

Правильный ответ

1. Из точки вне плоскости проведены две наклонные, одна из которых равна 16 см и наклонена под углом 30 0 к плоскости. Определите длину второй наклонной, если её проекция на плоскость равна 6 см.

Ответ: 10 см.

• Ответ: 10 см.

2. Точка М удалена орт плоскости квадрата на расстоянии 12 см. Найдите расстояние от этой точки до вершин квадрата, если его площадь равна 50 см 2 .

• 14 см. 15 см. 18 см. 16 см. 13 см.
• 14 см.
• 15 см.
• 18 см.
• 16 см.
• 13 см.

Правильный ответ

2. Точка М удалена орт плоскости квадрата на расстоянии 12 см. Найдите расстояние от этой точки до вершин квадрата, если его площадь равна 50 см 2 .

Ответ: 13 см.

• Ответ: 13 см.

Видео-вопрос

Слайд 11

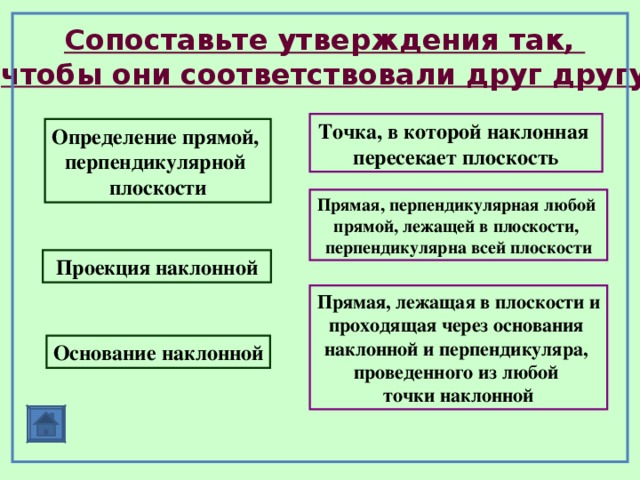
Сопоставьте утверждения так,

чтобы они соответствовали друг другу

Точка, в которой наклонная

пересекает плоскость

Определение прямой,

перпендикулярной

плоскости

Прямая, перпендикулярная любой

прямой, лежащей в плоскости,

перпендикулярна всей плоскости

Проекция наклонной

Прямая, лежащая в плоскости и

проходящая через основания

наклонной и перпендикуляра,

проведенного из любой

точки наклонной

Основание наклонной

Сделай рисунок

Даны четыре точки .

Как расположить эти точки,

чтобы получились четыре

прямоугольных треугольника?

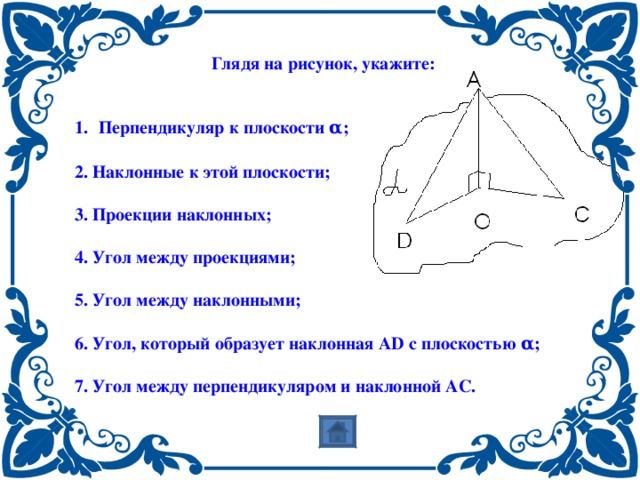
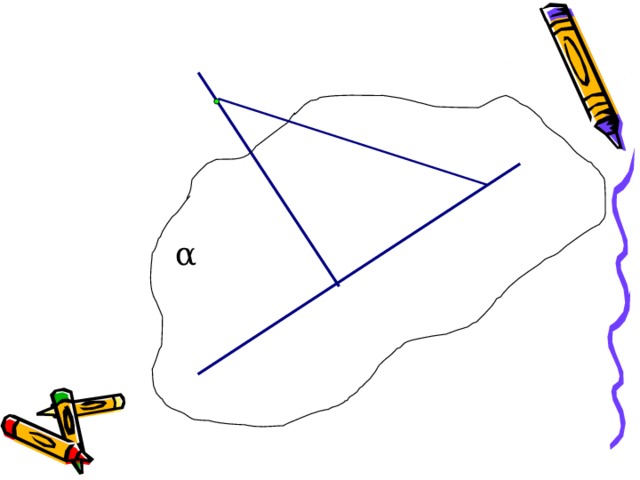
Глядя на рисунок, укажите:

• Перпендикуляр к плоскости α ;

2. Наклонные к этой плоскости;

3. Проекции наклонных;

4. Угол между проекциями;

5. Угол между наклонными;

6. Угол, который образует наклонная А D с плоскостью α ;

7. Угол между перпендикуляром и наклонной АС.

Получить шифровку

1

Г

2

И

3

4

Д

5

Я

6

Е

С

7

8

Ы

К

9

О

10

Т

11

12

В

Х

13

М

14

Р

15

Ж

16

17

Л

У

18

19

Ь

20

Ч

П

21

Н

22

А

1

5

9

13

5

10

14

2

4

5

6

10

18

2

6

8

17

6

6

10

11

9

20

14

22

11

2

16

18

21

9

14

22

6

6

17

15

3

22

10

18

21

22

21

5

20

14

22

11

2

16

18

21

7

12

19

5

14

10

5

15

22

12

Домашнее задание:

• Повторить определения пройденных тем.
• Решить задачу: Одна наклонная длиной 20 см образует с плоскостью угол 30 0 , другая наклонная угол 45 0 . Вычислите длину второй наклонной, если они выходят из одной точки.