систематизировать знания по теме;
- проверить усвоение знаний и умений применять свойства степени при решении упражнений
- ( x∙y ) 3 =х 3 ∙ у 3
- b 4 ∙ b 8 = b 12
- ( а 2 ) 4 = а 12
- p 10 : p 7 = p 3
5.
1 вариант
2 вариант
При умножении степеней
с одинаковыми
основаниями •
При делении степеней
с одинаковыми
основаниями •
При возведении
степени в степень •
При возведении
произведения в степень •
При возведении дроби в степень •
• основание остается прежним,
а показатели перемножаются
• в эту степень возводят каждый
множитель и результаты перемножают
• основание остается прежним,
а показатели складываются
• в эту степень возводят числитель
и знаменатель и
результаты делят
• основание остается прежни,
а показатели вычитаются
При __________ степеней с одинаковыми основаниями, основание _______________ , а показатели степеней складываются.
При делении степеней с ____________ основаниями, основание ___________________ , а показатели степени _______________ .
При _________________________ _ основание остается прежним, а показатели степеней перемножаются.
При возведении в степень произведения, в эту степень ______________________ и результаты _________________ .
При возведении в степень дроби, возводят в эту степень ___________________________ и результаты ____________________________ .
3 5∙2
3 5 . 3 2
5 7 ∙11 7
11 7 . 11 5
2 5. 3 5
11 5∙7
3 5 : 3 2
11 7 : 11 5
2 5: 3 5
11 7 -5
(2 . 3) 5
(5 . 11) 7
3 2+5
(3 2 ) 5
11 7+5
(11 5 ) 7
7
5 7: 11 7
5
3 5-2
2 вариант
1 вариант
При умножении степеней
с одинаковыми
основаниями •
При делении степеней
с одинаковыми
основаниями •
При возведении
степени в степень •
При возведении
произведения в степень •
При возведении дроби в степень •
• основание остается прежним,
а показатели перемножаются
• в эту степень возводят каждый
множитель и результаты перемножают
• основание остается прежним,
а показатели складываются
• в эту степень возводят числитель
и знаменатель и
результаты делят
• основание остается прежни,
а показатели вычитаются
При умножении степеней с одинаковыми основаниями, основание остается прежним, а показатели степеней складываются.
При делении степеней с одинаковыми основаниями, основание остается прежним, а показатели степени вычитаются.
При возведении степени в степень основание остается прежним, а показатели степеней перемножаются.
При возведении в степень произведения, в эту степень каждый множитель и результаты перемножают.
При возведении в степень дроби, возводят в эту степень и числитель и знаменатель и результаты записывают в числитель и знаменатель.
3 5∙2
3 5 . 3 2
11 7 . 11 5
5 7 ∙11 7
2 5. 3 5
3 5 : 3 2
11 5∙7
11 7 : 11 5
2 5: 3 5
11 7 -5
(2 . 3) 5
(5 . 11) 7
11 7+5
3 2+5
(3 2 ) 5
(11 5 ) 7
5 7: 11 7
7
5
3 5-2
a 5 ∙ a 2 ∙ a 6 = a 13 n 15 : n 15 = n
( m 4 ) 6 = m 24 b ∙ b 2 b 3 = b 5
y 20 :y=y 20 y 7 : y 4 =y 3
(x 2 ) 3 =x 5
( y 2 ∙ x 5 ) 3 = y 6 ∙ x 15
a 5 ∙ a 2 ∙ a 6 = a 13 n 15 : n 15 = n
( m 4 ) 6 = m 24 b ∙ b 2 b 3 = b 5
y 20 :y=y 20 y 7 : y 4 =y 3
(x 2 ) 3 =x 5
( y 2 ∙ x 5 ) 3 = y 6 ∙ x 15
( a ∙ b 4 ) 4 ∙ a 5 ∙ b 2 =
a 4 ∙ b 16 ∙ a 5 ∙ b 2 = a 9 ∙ b 18
c 13 ∙ d 47
(-с d 8 ) 6 ∙ c 7 ∙ d 5 =
27∙ x 10 ∙ y 10
- x 5 ∙(-3 xy 2 ) 5 =
(2 x 3 ∙ y ) 3 ∙(3 x 2 ∙ y 5 ) 2 =
72 x 13 ∙ y 13
( a 3 ) 5 ∙( d 4 ) 2
1
( a 2 d ) 8
a
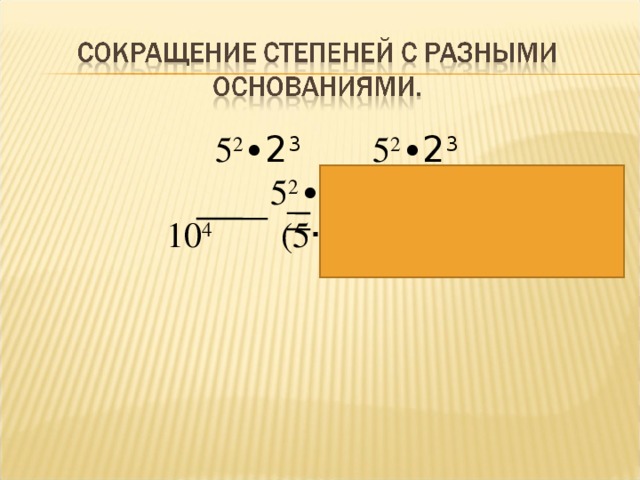
5 2 ∙2 3 5 2 ∙2 3 5 2 ∙2 3
10 4 (5 ∙ 2) 4 5 4
1
50
2 4
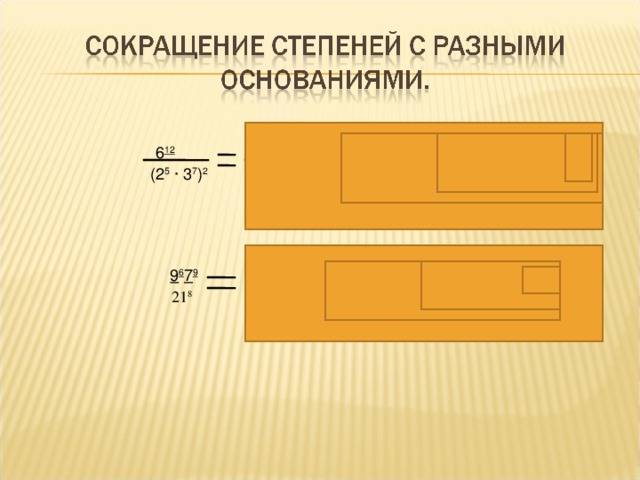
(2∙3) 12
4
2 12 ∙ 3 12
2 10
6 12
∙ 2 2 ∙ 3 12
9
(2 5 ∙ 3 7 ) 2
2 10 ∙ 3 12 ∙ 3 2
2 10 ∙ 3 14
(2 5 ∙ 3 7 ) 2
9 6 7 9
7
3 4
3 8
3 12 7 8 7
(3 2 ) 6 7 9
567
3 8 7 8
(3 ∙7) 8
21 8
3 8
Страница учебника 185
№ 5 и №6 для всех
№ 4 и №3 на выбор один по желанию.
1.На уроке я работал…
2.Своей работой на уроке я…
3.Урок для меня показался…
4.За урок я…
5.Мое настроение…
6.Материал урока мне был…
7.Домашнее задание мне кажется…
Получите свидетельство
Вход
Презентация к уроку алгебры на тему "Свойства степени с натуральным показателем" (2.02 MB)
0
581
54
Нравится
0
