Благодатнівська загальноосвітня школа I-III ступенів
“ Чому можна дивуватися дивлячись на світ?”
Методична розробка уроку з геометрії в 9 класі
Тема: « Правильні многокутники»
Підготувала : Бродяна Наталія Леонідівна
вчитель математики та інформатики
спеціаліст вищої категорії,
учитель - методист

Тема уроку . Узагальнюючий урок по темі «Правильні многокутники» Форма проведення: урок з комп’ютерною підтримкою, з використанням прикладного програмного забезпечення навчального призначення.
Мета уроку:
навчальна:
- повторити та закріпити весь теоретичний матеріал теми;
- сформувати вміння відтворювати вивчені формули, записувати їх відповідно до умови задачі;
- повторити формули залежності між стороною правильного многокутника і радіусом описаного( вписаного) кола;
- повторити побудову правильних многокутників ;
- формули залежності між сторонами правильного многокутника і його площею та периметром.
розвивальна:
- уміння застосовувати знання для розв’язання задач різного рівня складності;
- забезпечити розвиток аналітичного мислення на етапі засвоєння знань;
- уміти порівнювати на етапі практичної обробки результати розв’язування задач і вправ;
- розвивати пізнавальний інтерес учнів, вчити бачити зв'язок між математикою та навколишнім середовищем.
виховна:
- підтримувати інтерес до вивчення математики;
- виховувати культуру мовлення, уміння чітко висловлювати свої думки;
- розвивати навички самостійності і самоаналізу під час виконання практичних завдань;
- створювати умови для набуття досвіду самовизначення на етапі вільного вибору практичних самостійних завдань.
Вимоги до рівня підготовки учнів:
- формулюють означення правильного многокутника ; записують і пояснюють формули радіусів вписаного та описаного
- формулюють означення правильного многокутника ;
- записують і пояснюють формули радіусів вписаного та описаного
кіл правильного многокутника;
- кіл правильного многокутника;
- радіусів вписаного та описаного кіл правильного трикутника,
- радіусів вписаного та описаного кіл правильного трикутника,
чотирикутника (квадрата), шестикутника та доводять їх;
- чотирикутника (квадрата), шестикутника та доводять їх;
- алгоритми побудови правильного трикутника , чотирикутника та
- алгоритми побудови правильного трикутника , чотирикутника та
шестикутника;
- записують і пояснюють формули довжини кола і дуги кола; формулюють теорему про відношення довжини кола до його
- записують і пояснюють формули довжини кола і дуги кола;
- формулюють теорему про відношення довжини кола до його
діаметра;
- дають означення кругового сектора і сегмента; записують і пояснюють формули площі круга , сектора і сегмента.
- дають означення кругового сектора і сегмента;
- записують і пояснюють формули площі круга , сектора і сегмента.

Тип уроку: узагальнення й систематизації знань і вмінь.
Наочність і обладнання: комп’ютер, інтерактивна дошка, мультимедійний проектор,
ППЗ- Геометрія , 9 клас,
презентація «Правильні многокутники",
шаблони правильних многокутників:
трикутник, квадрат, шестикутник,
п’ятикутник восьмикутник, многогранники,
презентація “Геометрія бджолиних сот,
правильні паркети”

I.Організаційний момент Со времён Пифагора известны они. В них равные стороны и равны углы. Их встретим в орнаментах и на паркетах В стихотворениях разных поэтов. И даже пчелы с ними работают, Строя в их форме домики- соты О.Панишева
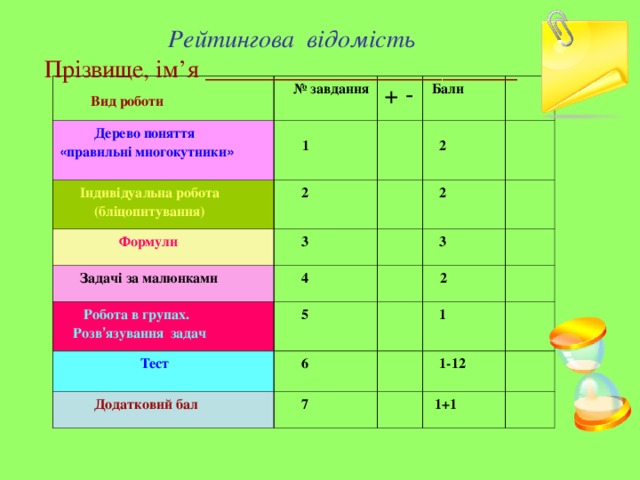
Рейтингова відомість Прізвище, ім’я _________________________
Вид роботи
№ завдання
Дерево поняття
« правильні многокутники »
1
Індивідуальна робота
+ -
(бліцопитування)
2
Формули
Бали
2
3
Задачі за малюнками
4
2
Робота в групах.
3
Розв ’ язування задач
5
Тест
2
6
Додатковий бал
1
7
1-12
1+1

Чому можна дивуватися
дивлячись на світ ?
Основоположне запитання

II.Актуалізація опорних знань учнів. 1. Повторення теоретичного матеріалу - використання ППЗ- Геометрія , 9 клас. 2. Бліцопитування

1 . Який многокутник називається правильним?
2 .Чи вірно , що любий рівносторонній трикутник являється правильним?
3 .Чи вірно, що любий рівносторонній чотирикутник являється правильним?
4 .Який многокутник називається вписаним в коло?
5. Який многокутник називається описаним навколо кола?
6. Знайдіть величину внутрішнього кута при будь – якій вершині правильного :
а)трикутника; б)чотирикутника; в)шестикутника.
6. Знайдіть величину зовнішнього кута при будь – якій вершині правильного :
а)трикутника; б)чотирикутника; в)шестикутника
7.Визначте вид многокутника, якщо :
- кожний внутрішній кут дорівнює 60°; 90°;120°;
- кожний зовнішній кут дорівнює120°; 90° ; 60°;
- радіус вписаного кола в два рази більше радіуса описаного кола;
- кожна сторона дорівнює радіусу описаного кола;
- із кожної вершини многокутника можна провести дві діагоналі.

Які величини можна обчислити за слідуючими формулами:

Установіть відповідність між числом (1-13) та множиною, до якої воно
належить (А-О)
1 А - площа круга
Б – довжина кола
2
А Б В Г Д Е Ж З К Л М Н О
1
2
3
4
5
6
7
8
9
10
11
12
13
В – довжина дуги
3 кола
4 Г- площа сегмента ,
меншого за півкруг
Е - площа сегмента,
6 коли сегмент є півкругом .
5 Д- площа правильного
многокутника
Ж – радіус вписаного
7 кола
8 З-довжина кола
11 М- сторона правильного
многокутника
9 К- площа кругового
сектора
10 Л- площа круга
Н- площа сегмента ,
12 більшого за півкруг
О - формула для обчислення кута
13 правильного многокутника
.
сектора
10 Л - площа круга
11 М - сторона правильного
многокутника
Н - площа сегмента ,
12 більшого за півкруг
О - формула для обчислення кута
13 правильного. многокутника ;
.

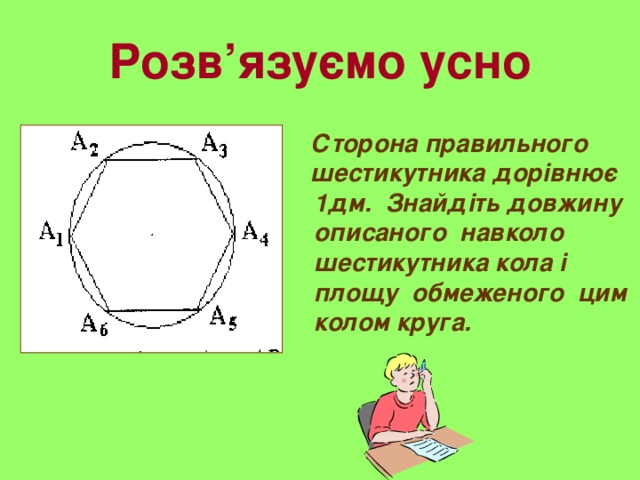
Розв’язуємо усно
Сторона правильного
шестикутника дорівнює 1дм. Знайдіть довжину описаного навколо шестикутника кола і площу обмеженого цим колом круга.
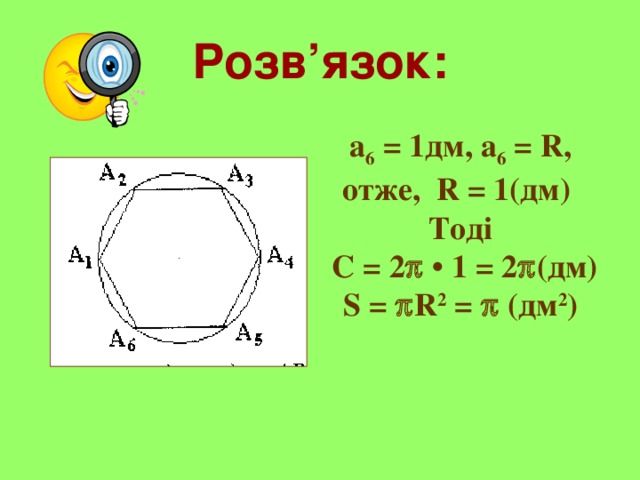
Розв’язок:
а 6 = 1дм, а 6 = R,
отже, R = 1(дм)
Тоді
С = 2 • 1 = 2 (дм)
S = R 2 = (дм 2 )
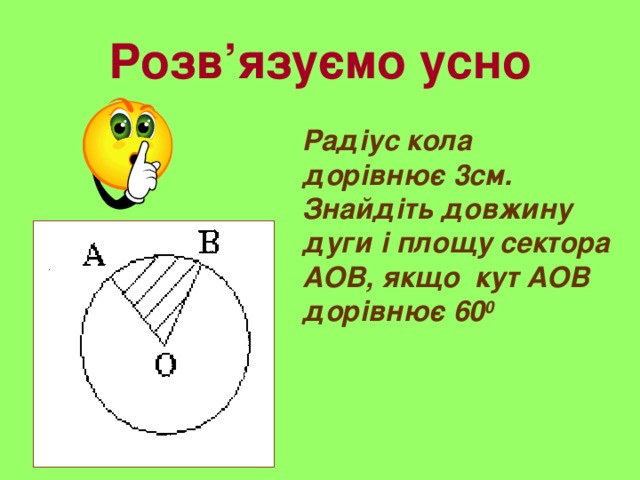
Розв’язуємо усно
Радіус кола дорівнює 3см. Знайдіть довжину дуги і площу сектора АОВ, якщо кут АОВ дорівнює 60 0
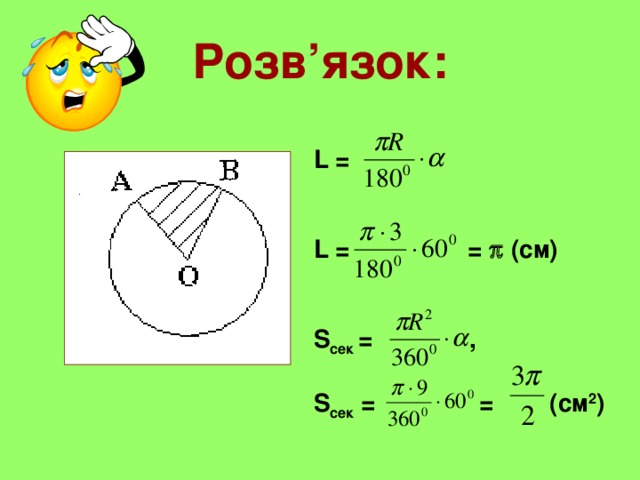
Розв’язок:
L =
L = = (см)
S сек = ,
S сек = = (см 2 )

Розв’язуємо усно
Знайдіть площу заштрихованої фігури , якщо сторона квадрата дорівнює 4см.
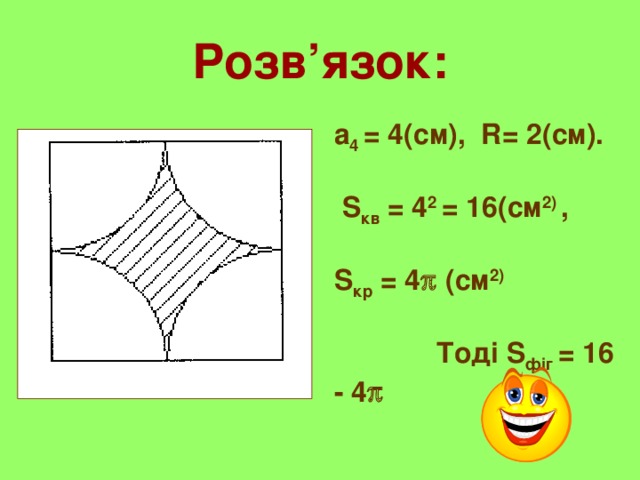
Розв’язок:
а 4 = 4(см), R= 2(см).
S кв = 4 2 = 16(см 2) ,
S кр = 4 (см 2)
Тоді S фіг = 16 - 4

Розв’язуємо усно
Зіниця людського ока в залежності від степеня яскравості світла змінюється в розмірі від 2 мм до 6 мм. У скільки разів площа розширеної зіниці більша від площі звуженої?

Розв’язок:
- S = = (мм 2 )
- D =6(мм), S = = 9 (мм 2 )
- 9 : = 9 (разів)

Розв’язуємо усно
Знайдіть площу кільця , якщо радіус більшого кола дорівнює 5дм, а радіус меншого кола дорівнює 4дм .

Розв’язок:
- S кіл. = S в. кр. – S м. кр.
- 25 - 16 = 9 (дм 2 )

Тестування. Задачі для самостійного розв’язування
- 1.Навколо правильного трикутника описано коло і в нього вписано коло. Довжина меншого кола дорівнює см. Знайдіть площу утвореного кільця і площу трикутника.
- 2. Навколо правильного трикутника описано коло і в нього вписано коло. Сторона трикутника дорівнює 4 см . Знайдіть площу утвореного кільця , довжину меншого кола і площу трикутника.
- 3. Навколо правильного трикутника описано коло і в нього вписано коло. Площа меншого круга складає кв.см Знайдіть площу трикутника.
- 4. Навколо правильного трикутника описано коло і в нього вписано коло. Площа більшого круга складає кв.см. Знайдіть площу трикутника.
- 5.Знайдіть площу круга, вписаного у квадрат зі стороною 4 см.
- 6 Знайдіть площу круга, описаного квадрата зі стороною см.
- 7. Знайдіть площу круга, який вписано у правильний 6-кутник зі стороною 8 см.
8 . Знайдіть площу круга, який описаного навколо правильного 6-кутника зі стороною см.

Чому можна дивуватися
дивлячись на світ?
Основоположне запитання

Геометрія бджолиних сот
Чому бджоли “вибрали “ собі для комірок на сотах форму правильного шестикутника?

Із всіх правильних многокутників тільки трикутниками , квадратами і шестикутниками можна заповнити площину без пробілів і накладань.
Так як в цьому випадку сума кутів, що сходяться в одній вершині, дорівнює 360˚
(60˚·6=360˚; 90˚·4=360˚; 120˚·3=360˚).
Ось чому бджоли повинні « вибрати» одну із цих
фігур
Висновок: Будуючи шестикутні комірки бджоли більш економно використовують площу всередині невеликого вулика і воск для виготовлення комірок.
Чарльз Дарвін відмічав : « Далее этой ступени совершенства в архитектуре естественный отбор не мог вести, потому что соты пчёл абсолютно совершенны с точки зрения экономии труда и воска»
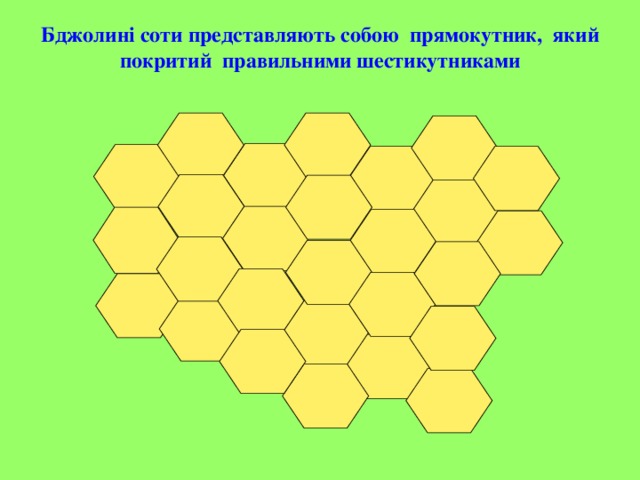
Бджолині соти представляють собою прямокутник, який покритий правильними шестикутниками

Скажіть, будь ласка, а де людина може використовуючи властивість правильних многокутників, покривати площину без просвітів ?
- Вірно. Якщо розташувати різні фігури одну біля одної в деякій послідовності , можна одержати дуже красиві орнаменти. Такі орнаменти любили стародавні римляни, які прикрашали ними стіни та стелю своїх будинків. Орнаменти із мозаїки зустрічаються і в наші дні. Ними прикрашають не тільки стіни, стелю, але і підлогу.
- Орнамент, який покриває підлогу називається
паркетом.
- Але паркет можна викласти не тільки із прямокутних дощечок, а і із різних правильних многокутників з однаковими сторонами, якщо їх викладати в певному порядку.
Паркет із правильних многокутників
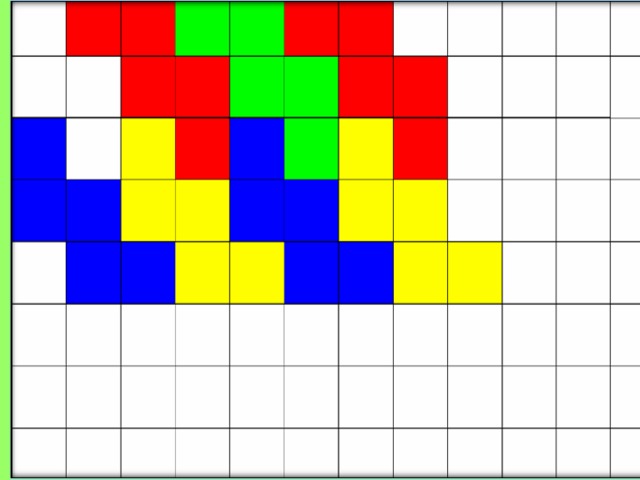
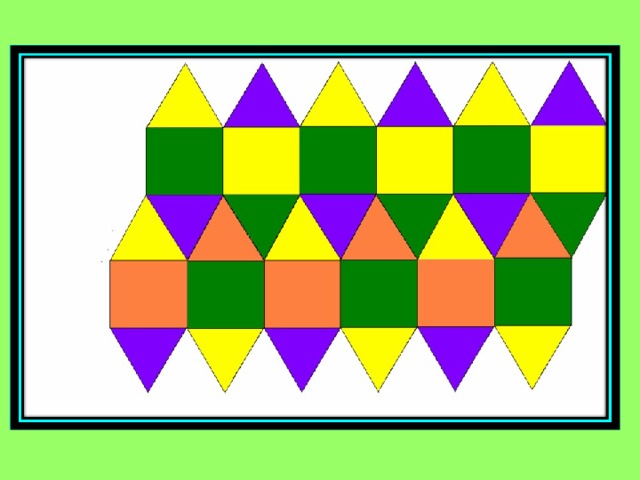
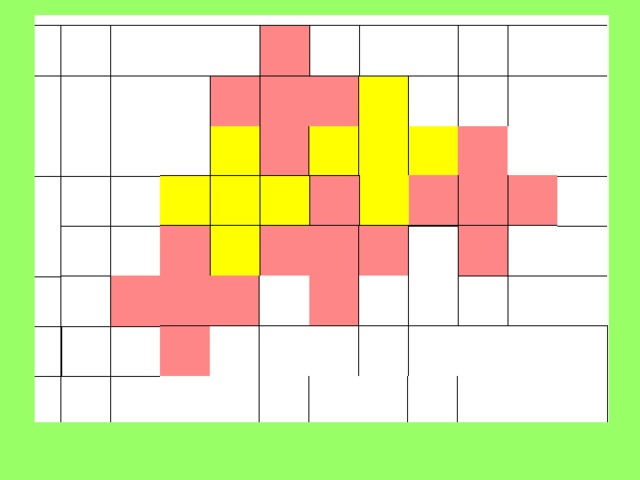


Двухцветные паркеты получаются из квадратов или правильных
треугольников, в большинстве своем разделенных на два равных треугольника.


Паркет може бути складений і із різних частин фігур
Наприклад, ці паркети отримали із трикутної сітки об’єднанням частини трикутників в шестикутники . Таким чином можна побудувати множину паркетів із правильних трикутників і шестикутників .



Наступні паркети мають таку властивість , що в кожному вузлі сходиться однакова кількість правильних многокутників одного й того ж виду


Правильні паркети

Паркет , який склали із правильних
восьмикутників і квадратів
42
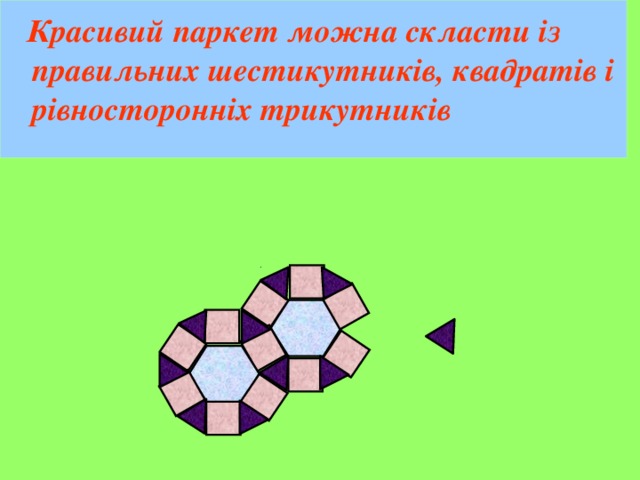
Красивий паркет можна скласти із правильних шестикутників, квадратів і рівносторонніх трикутників

Многогранник Правильним многогранником називається многогранник, в основі якого лежить правильний многокутник
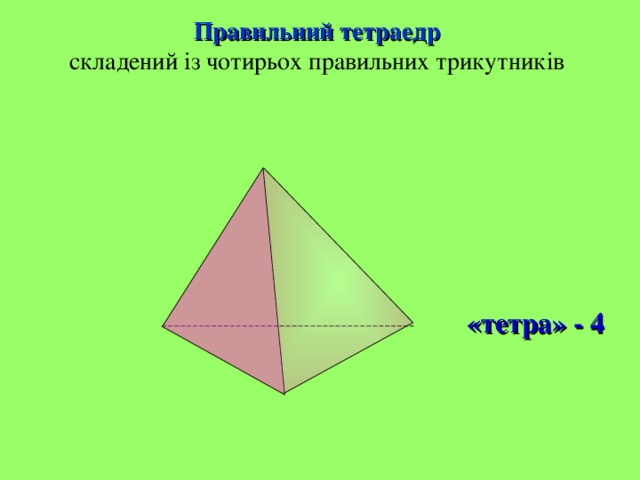
Правильний тетраедр складений із чотирьох правильних трикутників
«тетра» - 4

Куб, гексаэдр Куб складений із шести квадратів
«гекса» - 6
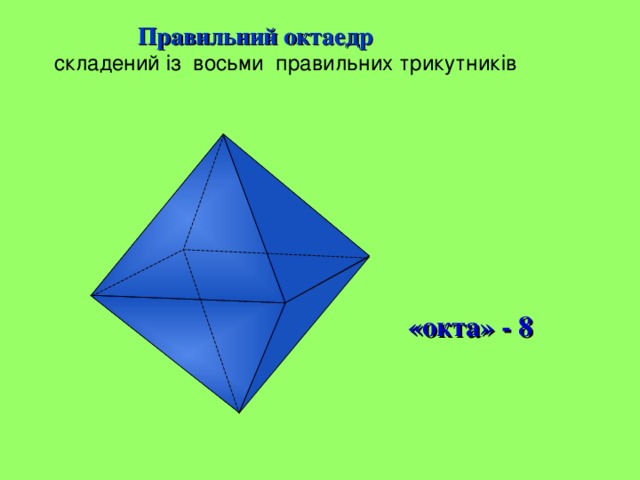
Правильний октаедр
складений із восьми правильних трикутників
«окта» - 8

Правильний ікосаедр складений із двадцяти правильних трикутників
«икоса» - 20

Правильний додекаедр складений із дванадцяти правильных шестикутників
«додека» - 12

Колективно даємо відповідь на питання: «Чому можна дивуватися дивлячись на світ?»

Першим властивості правильних многогранників описав давньогрецький вчений Платон. Саме тому правильні многогранники називають теж тілами Платона.
Платон вважав, що світ будується із чотирьох «стихій» - вогню, землі, повітря і води, а атоми цих «стихій» мають форму чотирьох правильних многогранників.
Платон
428 – 348 р. до н.е.
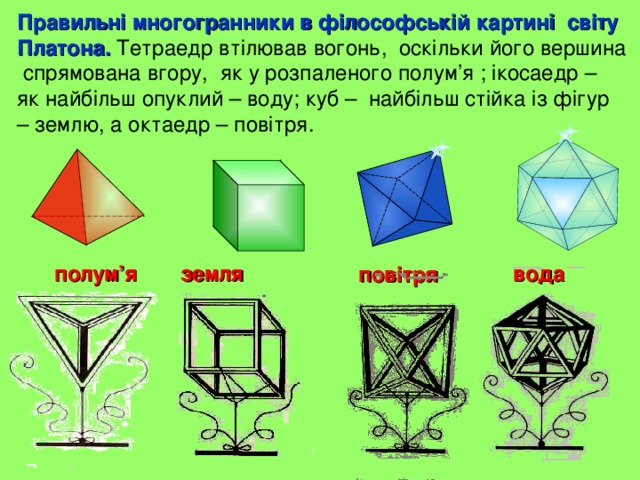
Правильні многогранники в філософській картині світу Платона. Тетраедр втілював вогонь, оскільки його вершина спрямована вгору, як у розпаленого полум ’ я ; ікосаедр – як найбільш опуклий – воду; куб – найбільш стійка із фігур – землю, а октаедр – повітря .
земля
полум ’ я
вода
повітря
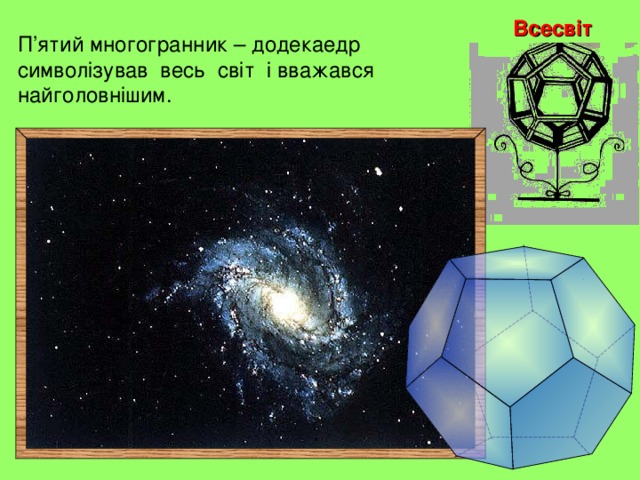
Всесвіт
П’ятий многогранник – додекаедр символізував весь світ і вважався найголовнішим.

Великий інтерес до форм правильних многогранників проявляли скульптори, архітектори, художники. Їх вражало досконалість, гармонія многогранників. Леонардо да Вінчі (1452 – 1519) захоплювався теорією многогранників і часто відтворював їх на своїх полотнах. Сальвадор Далі на картині «Тайная вечеря» відтворив І. Христа із своїми учениками на фоні величезного прозорого додекаедра.

Підбиття підсумків уроку
- Учитель з учнями підводять підсумок по етапам уроку. Оцінки за урок виставляються не тільки за тестування, а і за участь в роботі на протязі всього уроку. Аналізується кожний вид роботи на уроці та виясняється, що потрібно зробити в майбутньому щодо покращення власного результату. Заповняються рейтингові відомості учнів та виставляються оцінки за урок до щоденника.

Домашнє завдання. Повторити конспекти, блок- схеми по темі « Правильні многокутники», підготуватися до виконання контрольної роботи. Варіант 6,7 із додаткової літератури.
Усна рефлексія
« Після цього уроку я зрозумів»
« Найбільше мене вразило на уроці»
« Я хочу більше дізнатись»


 Получите свидетельство
Получите свидетельство Вход
Вход



































































 Правильні многокутники (3.43 MB)
Правильні многокутники (3.43 MB)
 0
0 1317
1317 77
77 Нравится
0
Нравится
0


