Учитель: Григорьева Л.Н.
Предмет: алгебра и начала анализа
Учебный план – 5 часов в неделю (из них 3 ч. – алгебра и начала анализа, 2 ч. – геометрия)
Класс: 11
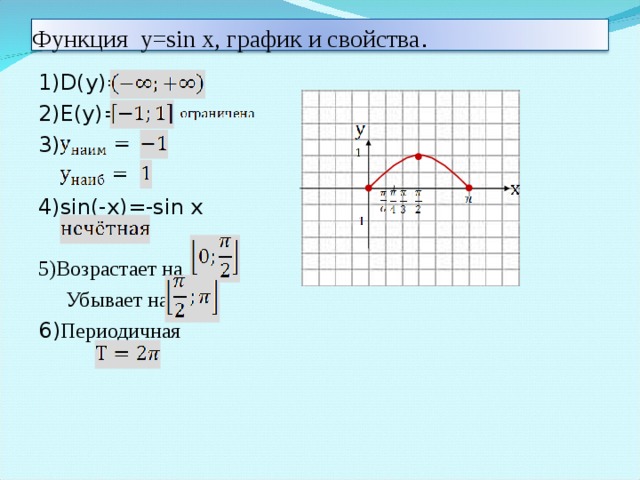
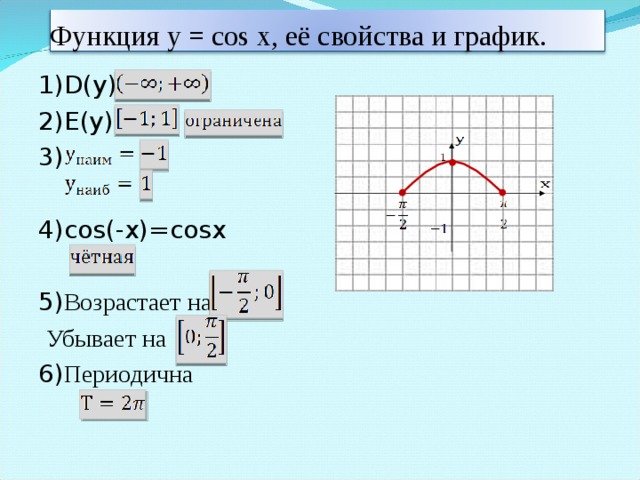
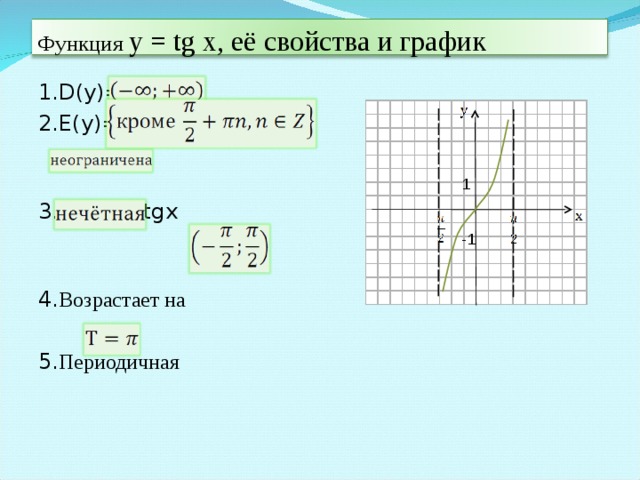
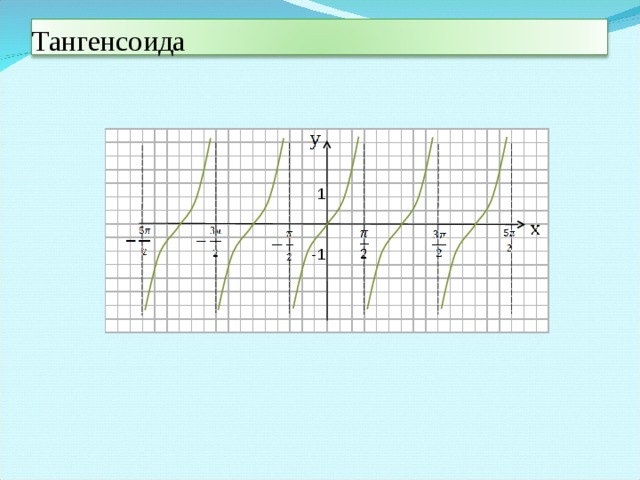
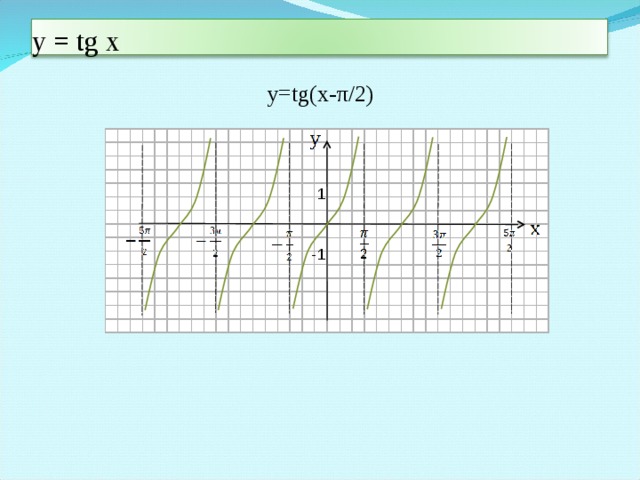
Тема: Повторение и обобщение «Тригонометрическая функция 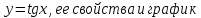 ».
».
Тип урока: проверка и оценка знаний и способов деятельности учащихся.
Цели урока:
дидактическая: обеспечить проверку и оценку знаний учащихся по теме; продолжить формирование умений по нахождению корней тригонометрических уравнений; по решению тригонометрических неравенств и систем неравенств; по использованию свойств тригонометрических функций при решении уравнений и преобразовании выражений; устойчивую мотивационную среду, интерес к изучаемой теме.
Развивающая: развивать у учащихся умение; образное мышление, навыки в применении знаний решения уравнений, неравенств, систем неравенств с целью подготовки к успешной сдаче экзамена по алгебре; способность к рефлексии.
Воспитательная: воспитывать аккуратность, самостоятельность, волю и настойчивость для достижения конечных результатов; умение общаться.
| Этапы урока и их содержание | Время (мин) | Деятельность | |
| учителя | учащегося | ||
| I. Организационный этап
II. Постановка цели Ребята, надеюсь, вы в хорошем настроении? Знаете, однажды французский писатель Анатоль Франс заметил: « Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам при сдаче экзаменов. Сегодня урок посвящен теме «Тригонометрическая функция
III. Устная работа Повторение теоретического материала и его применение на простых примерах. (приложение А) Повторение пройденного материала по слайдам и на карточке подписывают 3 графика
IV. Выполнение упражнений Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед. Поэтому сегодня будем не наблюдать, а большую часть урока работать самостоятельно. 1.Решите уравнение: (Приложение Б) с последующей проверкой
Проверка работ. Показ на слайде. (Приложение В)
Физпауза Посмотрите на числовую окружность, «нарисуйте» её глазами. Мысленно закрасьте каждую четверть разными цветами.
2. Решите неравенство (первый уровень). Решите систему неравенств (второй уровень). (Приложение Г) с последующей проверкой
Проверка работ. Показ на слайде. (Приложение Д)
V.Постановка цели Герберт Спенсер, английский философ, говорил: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы».
Сейчас мы попробуем применить полученные знания к решению заданий из ЕГЭ. В карточке всего 10 тестовых заданий, в первую часть входит 7 заданий средней сложности (0,5 баллов)). Для получения оценки 4 необходимо набрать 3, 5 балла. Оценка 5 ставится в том случае, если вы правильно выполнили математический диктант. (Приложение Е,Ж)
Полученный результат выполненной работы и является итогом урока. Он показывает насколько хорошо ученики разобрались с материалом.
VIII.. В заключении математический диктант: (Приложение Ж) IX.Домашнее задание творческого характера. Придумать пять тестовых заданий по теме.
X.Решение тригонометрических уравнений и неравенств требует от обучающихся хороших теоретических знаний, умений применять их на практике, требует внимания, трудолюбия, сообразительности. Именно по этой причине уравнения и неравенства, аналогичные рассмотренным на уроке, включаются в задания при сдаче ЕГЭ. Сегодня на уроке все очень хорошо поработали, четыре человека получили оценки. Молодцы, ребята! Урок окончен. Спасибо за урок. Рефлексия урока. Каждый ученик, выходя из класса, отмечает на диаграммах, изображенных на доске, свое личное отношение к уроку.
Было на уроке: трудно, обычно, легко. (Приложение З)
| 1
3
7
6
5
1
10
5
1
3
20
3
7
2
2
2 | Организационная
Сообщает тему урока, дату проведения урока, цель урока Слайд 1
Слайд 4 Проводит фронтальную беседу по теоретическим вопросам
Слайд 5
Следит за грамотным решением предложенных уравнений, проверяет индивидуальные решения уравнений обучающихся, работающих на боковой доске по карточке и в тетрадях
Использует медиапроектор Комментирует решения Слайд 11
Следит за грамотным решением предложенных неравенств, проверяет индивидуальные решения неравенств обучающихся, работающих на боковой доске по карточке и в тетрадях
Слайд 15 Использует медиапроектор Комментирует решения
Сообщает правила заполнения бланков регистрации
По окончании данного времени даёт ключ ответов
Выставляет оценки за работу
Поясняет домашнее задание, обращая внимание обучающихся на то, что аналогичные задания выполнялись на уроке.
Отмечает своё отношение к уроку | Сообщают об отсутствующих Записывают в тетради
Принимают активное участие в устном теоретическом опросе
2 человека работают на боковой доске, один обучающийся с помощью формул, второй с помощью числовой окружности, остальные записывают решения уравнений в тетрадях, выбирая любой метод решения
Один ученик устно объясняет решение Обучающиеся проверяют решения
Обучающиеся проводя зарядку для отдыха глаз
2 человека работают на боковой доске, один обучающийся с помощью формул, второй с помощью числовой окружности, остальные записывают решения уравнений в тетрадях, выбирая любой метод решения
Один ученик устно объясняет решение Обучающиеся проверяют решения
Отдых обучающихся
Организационная
Заполняют бланки регистрации
Обучающиеся выполняют задания, по окончании данного времени заканчивают работу, проверяют решение по данному ключу.
Прослушав пояснение учителя, записывают домашнее задание
Каждый ученик отмечает своё отношение к уроку |
Приложение А
Отметьте на числовой окружности точку М(t), если t =
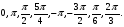
Что мы называем синусом? Косинусом? Вычислите sin t, cos t.
Может ли косинус быть равным: а) 0,75; б)
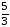 ? Почему?
? Почему?Может ли синус быть равным: а) -3,7; б)
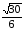 ? Почему?
? Почему? В какой четверти находится Рt , если
а) sin t 0, cos t 0;
б) sin t 0, cos t 0;
в) sin t 0, cos t 0;
г) sin t 0, cos t 0;
6. Упростите, объясняя, выражение: а) 1 + sin2 α + cos2 α;
б) 1 – sin2 α – cos2 α.
7. Имеет ли смысл выражение: а)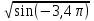
б)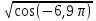 ? Объясните.
? Объясните.
8. Найдите наибольшее значение выражения: а) 2 sin t; б) – 3 cos t.
Приложение Б
| 1 вариант | 2 вариант | ||
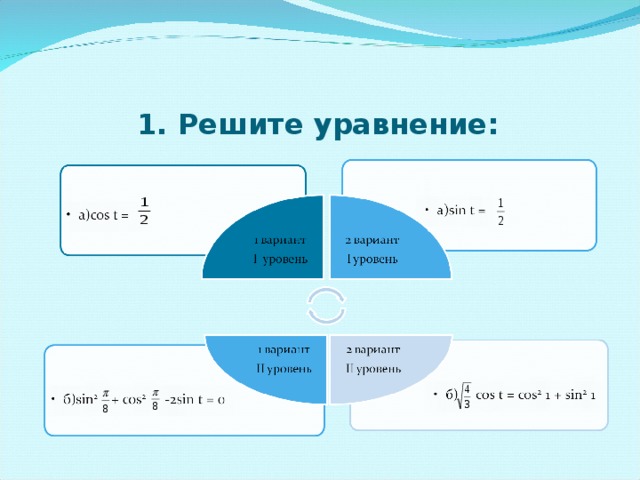
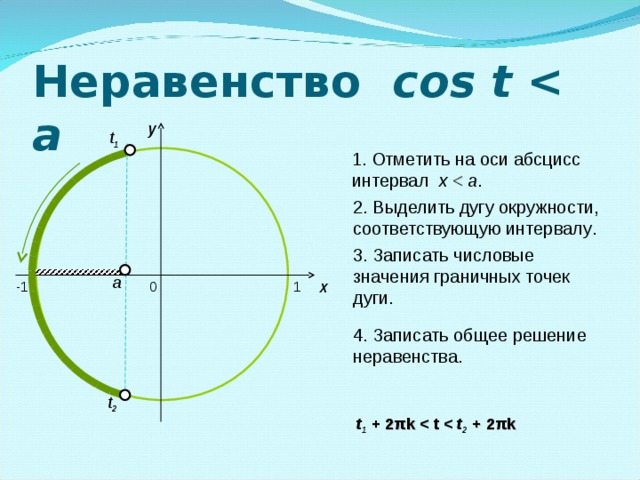
| I уровень | a)cos t = | I уровень | a)sin t = |
| II уровень | б)sin2 | II уровень | б) |
Карточки - инструкции по необходимости.


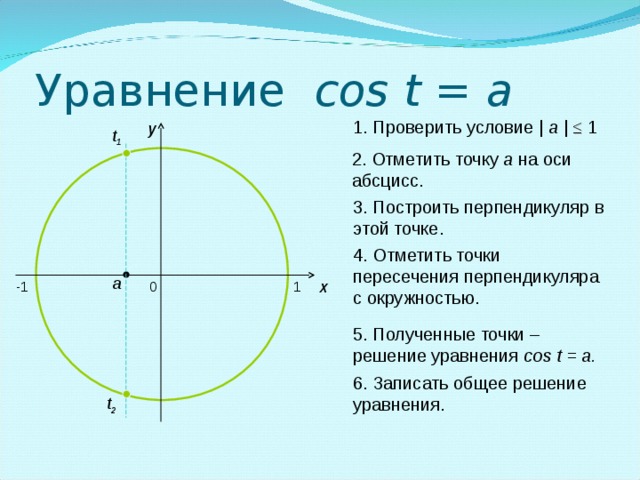
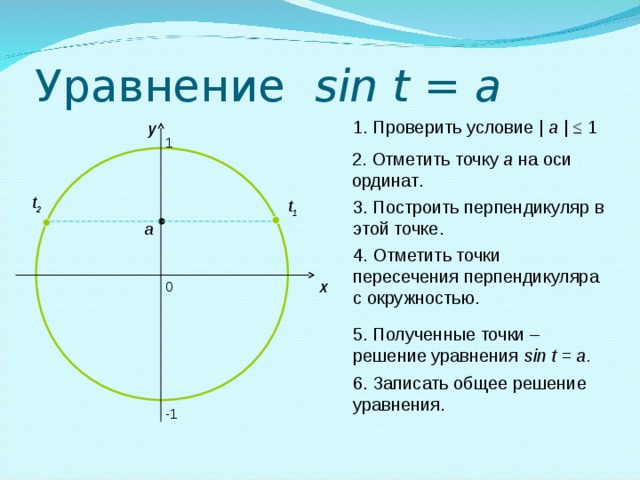
Приложение В
Приложение Г
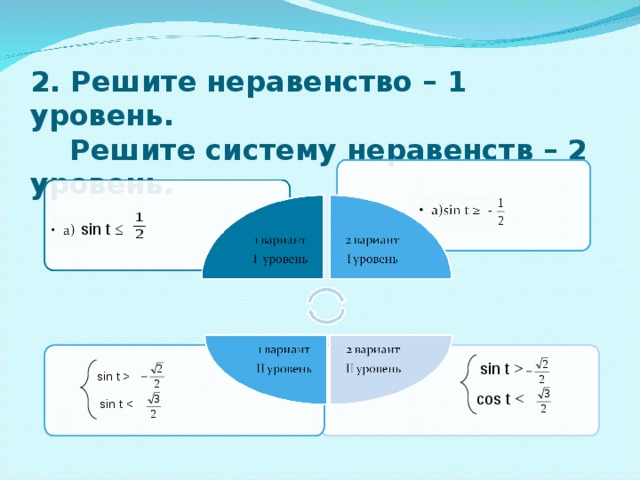
| 1 вариант | 2 вариант | |||
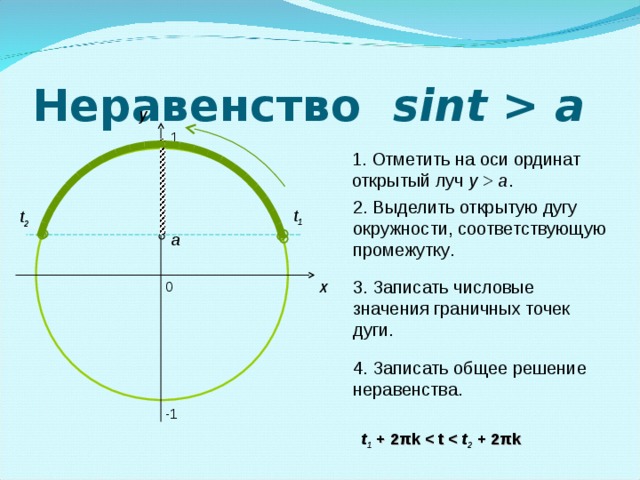
| I уровень | sin t ≤ | I уровень | sin t ≥ - | |
| II уровень |
sin t . | II уровень |
cos t . | |
Карточки - инструкции по необходимости.

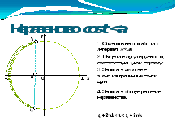
Приложение Д

Приложение Е
Часть I
| Инструкция для учащихся. Дайте краткий ответ.
| ||
| В1. Найдите значение выражения: 3sin2 α +10 + 3 cos2 α; |
| В1. |
| В2. Найдите значение выражения: 16 – 6sin2 α – 6cos2 α; |
| В2. |
| В3. Укажите ближайший к 0 корень уравнения 2 sin х + 1 = 0 |
| В3. |
| В4. Укажите ближайший к |
| В4. |
| В5. Найдите наибольшее значение выражения 3 + 4 cos t. |
| В5. |
| В6. Найдите наименьшее значение выражения 3 – 5 sin t. |
| В6. |
| В7. Найдите сумму корней уравнения cos(х + 2000π) = 0 |
| В7. |

Приложение Ж
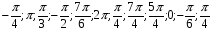
Приложение З
легко обычно трудно


 Получите свидетельство
Получите свидетельство Вход
Вход



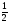
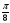
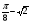 sin t = 0
sin t = 0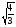 cos t = cos
cos t = cos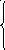
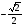 ,
,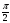 корень уравнения 2
корень уравнения 2 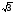 = 0
= 0


 0, cos t 0; б ) sin t 0, cos t 0; в ) sin t 0, cos t 0; г ) sin t 0, cos t 0; 6. Упростите, объясняя, выражение: а) 1 + sin 2 α + cos 2 α ; б) 1 - sin 2 α - cos 2 α . 7. Имеет ли смысл выражение: а) ; б) ? Объясните. 8. Найдите наибольшее значение выражения: а) 2 sin t ; б) - 3 cos t ." width="640"
0, cos t 0; б ) sin t 0, cos t 0; в ) sin t 0, cos t 0; г ) sin t 0, cos t 0; 6. Упростите, объясняя, выражение: а) 1 + sin 2 α + cos 2 α ; б) 1 - sin 2 α - cos 2 α . 7. Имеет ли смысл выражение: а) ; б) ? Объясните. 8. Найдите наибольшее значение выражения: а) 2 sin t ; б) - 3 cos t ." width="640"


 sin t sin t cos t
sin t sin t cos t

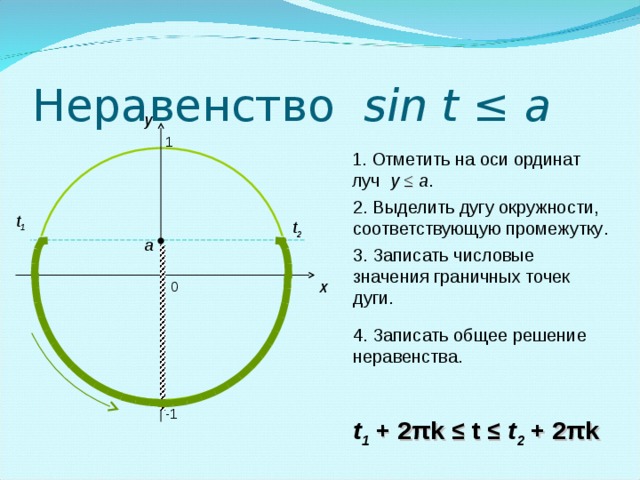
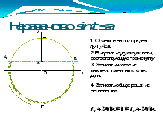
 a y 1 1 . Отметить на оси ординат открытый луч y a . 2 . Выделить открытую дугу окружности, соответствующую промежутку . t 1 t 2 a 3. Записать числовые значения граничных точек дуги . x 0 4. Записать общее решение неравенства . -1 t 1 + 2 π k t 2 + 2 π k" width="640"
a y 1 1 . Отметить на оси ординат открытый луч y a . 2 . Выделить открытую дугу окружности, соответствующую промежутку . t 1 t 2 a 3. Записать числовые значения граничных точек дуги . x 0 4. Записать общее решение неравенства . -1 t 1 + 2 π k t 2 + 2 π k" width="640"





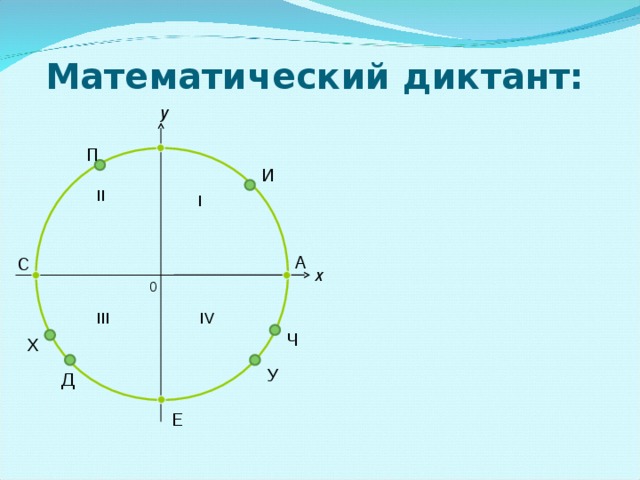
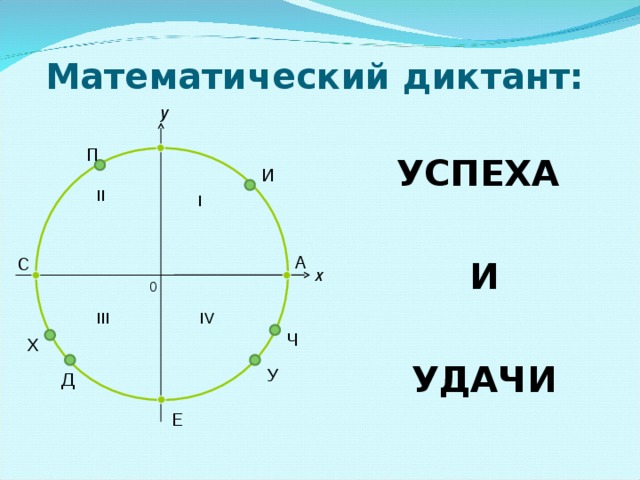










 Повторение и обобщение "Тригонометрическая функция у=tgx, ее свойства и график" (2.21 MB)
Повторение и обобщение "Тригонометрическая функция у=tgx, ее свойства и график" (2.21 MB)
 0
0 556
556 23
23 Нравится
0
Нравится
0


