Поурочный план.
Предмет: Математика.
6 класс.
Тема урока: «Обыкновенные дроби».
Тип урока: семинар – практикум.
Разработал:
учитель математики
высшей квалификационной категории
Старо-Семенкинского филиала
ГБОУ СОШ с Старый Маклауш
Клявлинского района Самарской области
Карнаухова Наталья Павловна
2014 Год
Тема урока: «Обыкновенные дроби».
Дидактическая цель и задачи урока:
Образовательные задачи
а) проконтролировать степень усвоения следующих основных знаний, умений и навыков , изученных и сформированных на предыдущем уроке: алгоритма нахождения части от числа ,алгоритма нахождения всего числа по его части, сведений о том , что одна и та же доля может быть представлена разными дробями
Б) углубить и систематизировать следующие специальные умения и навыки по данному учебному материалу:
: умение решать задачи на применение алгоритма нахождения части от числа, алгоритма нахождения всего числа по его части.
в) сформировать следующие общие учебные умения и навыки на материале этого урока :
умение понимать смысл каждой операции, её взаимосвязь с другими операциями, умение формулировать и конкретизировать задание, выделять этапы его выполнения , проводить аналогии и осуществлять перенос умений в новые условия.
Воспитательные задачи
А) В ходе урока содействовать повышению мотивации учебной деятельности за счёт нестандартной формы урока, развитию у детей нормальной самооценки.
Б) Осуществлять нравственное воспитание , в ходе урока содействовать формированию чувства товарищества , этических норм поведения .
В) В целях решения задач физического и санитарно- гигиенического воспитания , развития работоспособности , профилактики утомления своевременно и качественно провести физкультминутку, чередовать виды деятельности учащихся.
Задачи развития учащихся
а) – в целях решения задач развития у учащихся умений выделять главное , существенное в изучаемом материале ( формулирование самостоятельных выводов или контрольных вопросов, высказывания своего отношения к суждения ), формирование умений сравнивать , обобщать изучаемые факты и понятия организовать коллективное обсуждение заранее запланированных вопросов.
б)-для решения задачи развития у школьников самостоятельности мышления обеспечить в ходе урока групповые и индивидуальные формы работы учащихся ..
в)-обеспечить развитие речи учащихся ,
г)-формировать у школьников умения преодолевать трудности в учении , закалять волю , обеспечить ситуации эмоциональных переживаний
д)- для развития у учащихся познавательного интереса провести урок в нестандартной форме (семинара – практикума ).
3.Тип урока – семинар – практикум
4. структура урока:
- организация начала урока.
этап подготовки учащихся к активному и сознательному усвоению основных задач, входящих в содержание темы урока. постановка цели урока
этап проверки понимания учащимися нового материала, изученного на предшествующем уроке.
-этап формирования умений и навыков ( выполнение учащимися различных заданий, задач , упражнений ; проверка выполненных работ; обсуждение допущенных ошибок и их коррекция)
-этап информации учащихся о домашнем задании , инструктаж по его выполнению.
5.Общие методы, приёмы работы учеников:
самостоятельная работа учащихся над материалом, элементы теории параллельного воспроизведения материала, элементы алгоритмизации, частично-поисковый метод, учащиеся в поисках истины составляли схему-таблицу, делали выводы.
6.Средства наглядности: ЭВТ, учебник, рабочая тетрадь с печатной основой, слайдовая презентация урока.
Формирование УУД средствами учебного предмета «Математика »
| УУД |
| Типы заданий |
|
Личностные положительное отношение к урокам математики; умение признавать собственные ошибки; формирование ценностных ориентаций (саморегуляция, стимулирование, достижение и др.); формирование математической компетентности | Все без исключения задания ориентированы на достижение личностных результатов, так как они предлагают не только найти решение, но и обосновать его, основываясь только на фактах. Работа с математическим содержанием учит уважать и принимать чужое мнение, если оно обосновано. | Задания, сопровождаемые инструкцией «Объясни…», Обоснуй своё мнение…»
|
| Регулятивные отслеживать цель учебной деятельности ; учитывать ориентиры, данные учителем, при закреплении учебного материала; проверять результаты вычислений; адекватно воспринимать указания на ошибки и исправлять найденные ошибки. оценивать собственные успехи в вычислительной деятельности; планировать шаги по устранению пробелов .
| Одним из наиболее эффективных учебных заданий на развитие таких умений является текстовая задача, так как работа с ней полностью отражает алгоритм работы по достижению поставленной цели (по П.Я. Гальперину). Работа над системой учебных заданий (учебной задачей). | Текстовые задачи.
Задания, сопровождаемые инструкцией «Сравни свою работу с работами других ребят».
Проблемные вопросы для обсуждения учеников и выводы рядом со значком «!» на жёлтом поле, позволяющие проверить правильность собственных умозаключений. Таким образом, школьники учатся сверять свои действия с целью. Проблемные ситуации, позволяющие школьникам вместе с учителем выбрать цель деятельности (сформулировать основную проблему (вопрос) урока), авторские версии таких вопросов дают возможность оценить правильность действий учеников.
|
| Познавательные анализировать условие задачи (выделять данные и цель — что известно, что требуется найти); устанавливать закономерности ; понимать информацию, представленную в виде текста, схемы, таблицы; дополнять таблицы недостающими данными. видеть аналогии и использовать их при освоении приемов вычислений; конструировать геометрические фигуры из заданных частей; достраивать часть до заданной геометрической фигуры; мысленно делить геометрическую фигуру на части; сопоставлять информацию, представленную в разных видах; выбирать задание из предложенных, основываясь на своих интересах.
| Формирование моделирования как необходимого универсального учебного действия. Широкое использование продуктивных заданий, требующих целенаправленного использования и, как следствие, развития таких важнейших мыслительных операций, как анализ, синтез, классификация, сравнение, аналогия. Использование заданий, позволяющих научить школьников самостоятельному применению знаний в новой ситуации, т.е. сформировать познавательные универсальные учебные действия. умение понимать смысл каждой операции, её взаимосвязь с другими операциями, умение формулировать и конкретизировать задание, выделять этапы его выполнения , проводить аналогии и осуществлять перенос умений в новые условия.
| Задания с моделями: самостоятельное создание и их применение при решении предметных задач. Задания, сопровождающиеся инструкциями «Сравни», «Разбей на группы», «Найди истинное высказывание».
Задания линий «Занимательные и нестандартные задачи». |
| Коммуникативные сотрудничать с товарищами при выполнении заданий в паре: устанавливать и соблюдать очерёдность действий, сравнивать полученные результаты, выслушивать партнера, корректно сообщать товарищу об ошибках; задавать вопросы с целью получения нужной информации; организовывать взаимопроверку выполненной работы; высказывать свое мнение при обсуждении задания.
| Задания на развитие устной научной речи.
Задания на развитие комплекса умений, на которых базируется грамотное эффективное взаимодействие. | Задания, сопровождающиеся инструкциями «Расскажи», «Объясни», «Обоснуй свой ответ». Система заданий, нацеленных на организацию общения учеников в паре или группе (все задания, относящиеся к этапу первичного применения знаний; к работе над текстовой задачей, осуществляемой методом мозгового штурма) |
| Основой развития коммуникативных умений на данном уроке является использование на уроках трёх видов диалога: а) диалог в большой группе (учитель – ученики); б) диалог в небольшой группе (ученик – ученики); в) диалог в паре (ученик – ученик).
|
Предметные УУД
Знать алгоритма нахождения части от числа ,алгоритма нахождения всего числа по его части, сведений о том , что одна и та же доля может быть представлена разными дробями
уметь решать задачи на применение алгоритма нахождения части от числа, алгоритма нахождения всего числа по его части.
умение понимать смысл каждой операции, её взаимосвязь с другими операциями, умение формулировать и конкретизировать задание, выделять этапы его выполнения , проводить аналогии и осуществлять перенос умений в новые условия.
Организационный этап
Дидактическая задача этапа Подготовить учащихся к работе на урок.
Содержание этапа (1 слайд презентации).Деятельность учителя и учеников Взаимное приветствие учителя и учащихся : фиксация отсутствующих ,проверка внешнего состояния классного помещения ; проверка подготовленности учащихся к уроку; организация внимания ; внутренняя готовность , психологическая организация внимания.
Показатели выполнения дидактической задачи этапа. Кратковременность организационного момента ; полная готовность класса к работе ; быстрое включение учащихся в деловой ритм, организация внимания всех учащихся.
Способы активизации на этапе Сообщение консультантов о готовности класса
Время, отведённое на организационный этап.1 минута.
Этап подготовки учащихся к активному и сознательному усвоению основных задач, входящих в содержание темы урока
(мотивационный этап)
Дидактическая задача этапа: Организовать и направить к цели познавательную деятельность учащихся.
Показатели выполнения дидактической задачи этапа
Умение учителя чётко и однозначно определить образовательную цель урока , показать ученикам , чему они должны научиться в ходе урока , какими знаниями , умениями , навыками овладеть- от этого будет зависеть активность познавательной деятельности учащихся на последующих этапах.
| 2 этап | Деятельность учителя | Деятельность ученика. |
| Этап подготовки учащихся к активному и сознательному усвоению основных задач, входящих в содержание темы урока (мотивационный этап)
Время, отведённое на организационный этап.3 минута | Содержание этапа Запись на доске (слайде) цели урока. Учитель: «Сегодня мы с вами в процессе решения занимательных задач научимся применять алгоритм нахождения части от числа, алгоритм нахождения всего числа по его части, и знание о том, что одна и та же доля может быть представлена разными дробями» | Запомнить, понять, отслеживать цель учебной деятельности на протяжении всего урока |
Задание № 1. (мотивационный момент урока.)
Учитель предлагает учащимся упражнение, направленное на раскрепощение их мысли, на проявление инициативы, смелости при поиске решения.
«Отметить две точки и соединить их линией».
| Деятельность учителя | Деятельность учащихся |
|
Анализ работ учеников. Активные ученики достойны поощрения, так как одни из первых проявили смелость в оценке ситуации и приняли нестандартное решение. | а   ) Часть учеников класса осмелиться соединить заданные две точки ломанной ) Часть учеников класса осмелиться соединить заданные две точки ломанной
А В б) Ученик соединит две точки произвольной кривой
А В в) Ученик соединит две точки А и В кривой, которая образовала слова «Учитель» А В |
Этап проверки понимания учащимися нового материала, изученного на предшествующем уроке..
Дидактическая задача этапа
Установить, усвоили или нет учащиеся связь между фактами, содержание новых понятий, закономерности ; устранить обнаруженные пробелы .
Показатели выполнения дидактической задачи этапа
Проверка учителем не только объёма и правильности знаний, но также их глубины, осознанности, гибкости и оперативности. активная деятельность всего класса в ходе проверки знаний отвечающих учащихся.
Основной критерий выполнения дидактической задачи- уровень осознания нового материала большинством слабых и средних учеников.
Время, отведённое на организационный этап.8 минута.
Содержание этапа
Учитель предлагает учащимся упражнение, направленное на усвоение учащиеся связи между фактами, содержания новых понятий закономерностей.
воспроизведение учащимися знаний, умений и навыков, которые потребуются для выполнения предложенных заданий
Способы активизации на этапе
Взаимопроверка учащихся, направленная на выяснение положительных и отрицательных сторон в их знаниях, умениях и навыках и на указание того, что необходимо сделать для усовершенствования приёмов самостоятельной работы ;запись каждого упражнения и возможное решение на слайдах .
Задание № 1.
«Начертить прямоугольник, ширина которого 1 клетка, длина – 10 клеток и заштриховать 1/10 его часть».
| Деятельность учителя | Деятельность учащихся |
| Анализ работ учеников.
Если поддержать ребят, то учитель получит смелые, нешаблонные решения. | С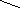 колько простора для творчества! колько простора для творчества! Возможные решения детей: а ) ) б) в)
|
Задание № 2.
| Деятельность учителя | Деятельность учащихся |
| Анализ работ учеников.
Не торопить, не ограничивая сроки сдачи работы, попросить закончить его дома, то многие ребята находят более сотни различных способов. |
Работа выполняется фломастерами самостоятельно.
Возможные работы детей появляются на слайде
|
«Нарисуйте квадрат, сторона которого 2 клетки. Заштрихуйте половину квадрата разными способами».
Этап формирования умений и навыков.
Дидактическая задача этапа Выполнение учащимися различных заданий ,задач ,упражнений; проверка выполненных работ ; обсуждение допущенных ошибок и их коррекция.
Время, отведённое на этап формирования умений и навыков.23 минуты
Содержание этапа
Учитель предлагает учащимся упражнение на усвоение алгоритма нахождения части от числа, смысла дроби, алгоритма нахождения всего числа по части, что целое содержит  и что одна и та же доля может быть представлена разными дробями.
и что одна и та же доля может быть представлена разными дробями.
Деятельность детей, в результате которой цель урока была достигнута. Ребята мысленно строили прямоугольники, делили его на число частей, сколько показывал числитель.
Задание № 1.
«Нарисовать прямоугольник 3 клетки на 4, заштриховать 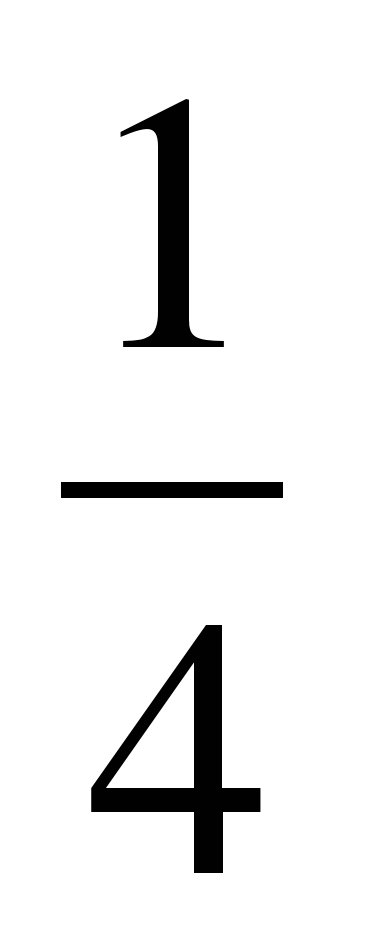 его часть».
его часть».
| Деятельность учителя | Деятельность учащихся |
| Вопросы детям. сколько всего клеток в прямоугольнике? Сколько клеток вы закрасите? Ответ: 12 : 4· 1=3 клетки | Работа выполняется фломастерами самостоятельно. Большинство учеников считают, сколько всего клеток в прямоугольнике. Затем находят по известному способу часть от части и заштриховывают три клетки.
Анализ работ учеников.
Возможные работы детей появляются на слайде |
Разумно предложить: «Не используя алгоритма нахождения дроби от числа, просто глядя на картинку, анализируя ее, выяснить, сколько клеток составляет 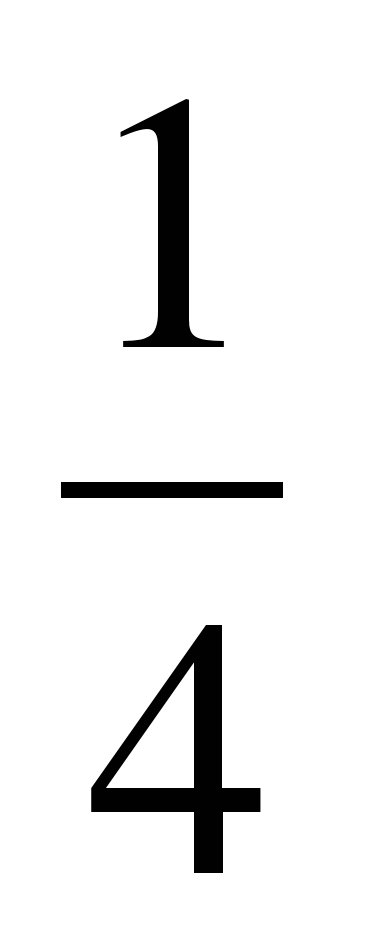 часть от всего прямоугольника?»
часть от всего прямоугольника?»
Возможное рассуждение ученика: «прямоугольник содержит 4 равных ряда по три клетки, значит, один ряд составляет  часть всего прямоугольника».
часть всего прямоугольника».
| Деятельность учителя | Деятельность учащихся |
| Учитель может получить и другие решения, если на их поиск обратить внимание учеников. | Работа выполняется фломастерами самостоятельно
Анализ работ учеников.
Возможные работы детей появляются на слайде
|
Задание № 2.
«Нарисовать прямоугольник 3 клетки на 4. заштриховать  и
и 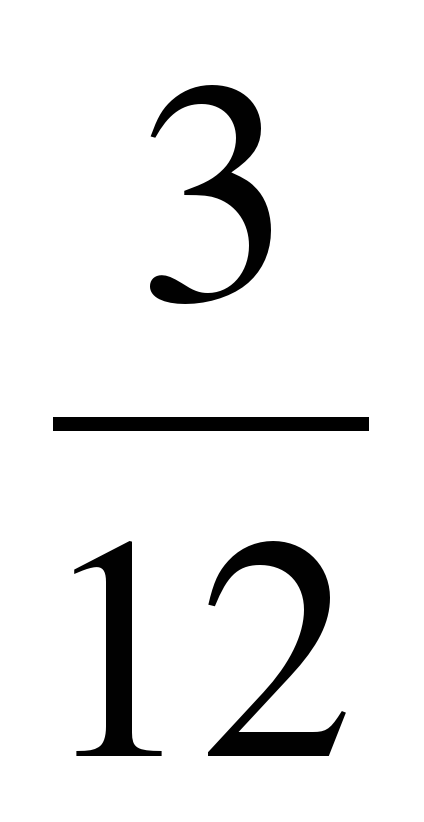 части прямоугольника разным цветом.
части прямоугольника разным цветом.
| Деятельность учителя | Деятельность учащихся |
| Организовать коллективный анализ полученных «картинок» Вопросы: 1)сколько всего клеток в прямоугольнике? 2) сколько клеток составляет  прямоугольника? прямоугольника? 3) а 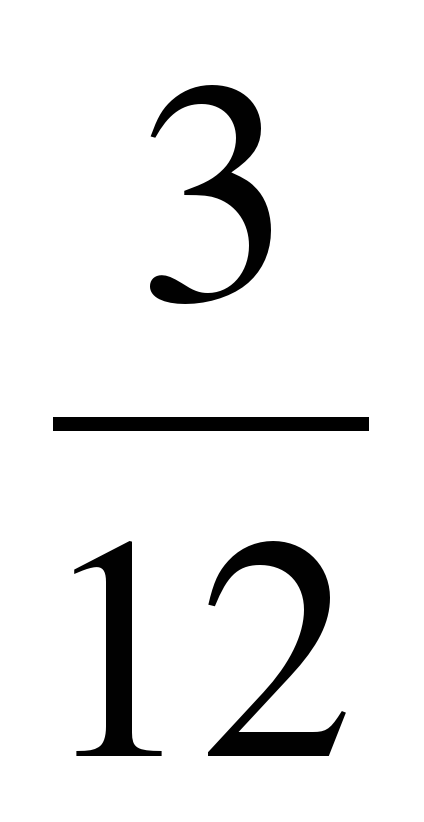 прямоугольника? прямоугольника? 4) а давайте сравним наши работы по закрашиванию 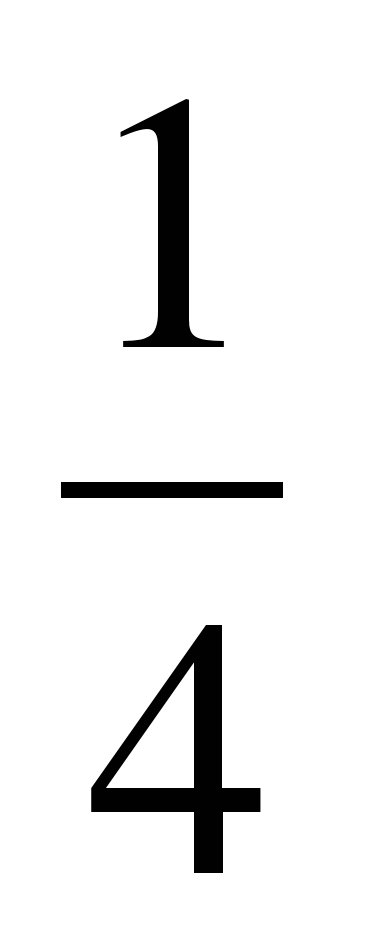 и и 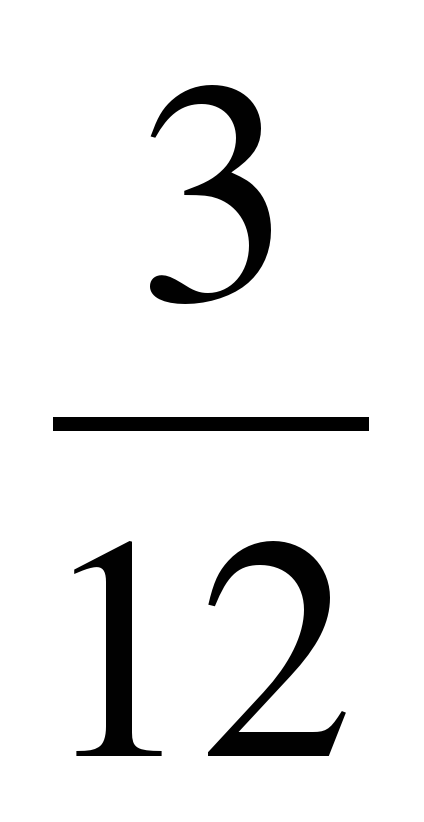 прямоугольника. прямоугольника. 5) смысл дроби 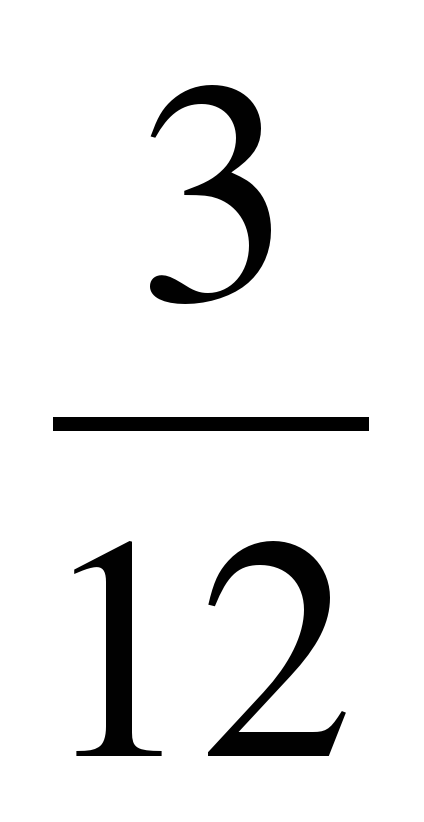 ? ? | 1.работа выполняется фломастерами самостоятельно
2.Ответы учеников: ученик: «В прямоугольнике всего 12 клеток» ученик: « прямоугольника составляет 1 клетку» прямоугольника составляет 1 клетку» ученик: «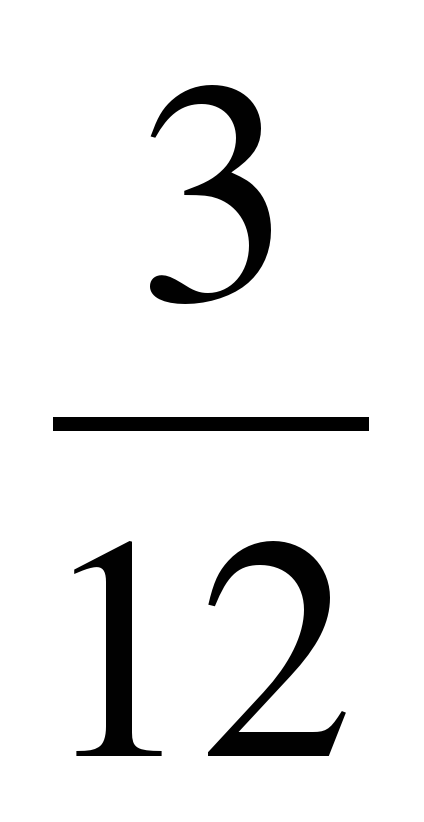 прямоугольника составляет 3 клетки» прямоугольника составляет 3 клетки» ученик: «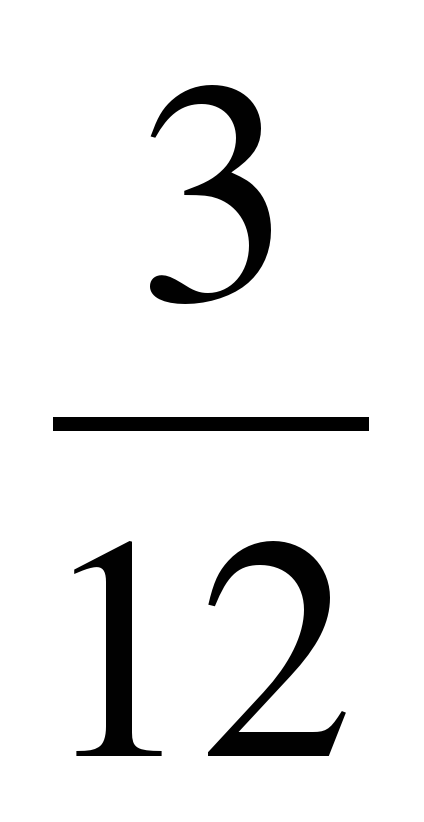 и и 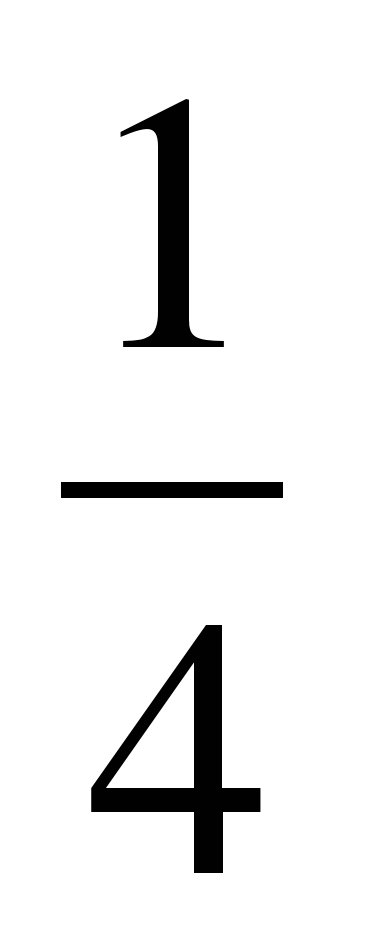 равны между собой» равны между собой» ученик: «Целое число надо разделить на 12 частей и взять 3 такие части». работа выполняется фломастерами самостоятельно
|
Задание № 3.
Практическая работа. (работа в парах)
А) «Начертить прямоугольник размером 6 клеток на 8 клеток»
Б) «Заштриховать  его часть красным цветом»
его часть красным цветом»
В) «Заштриховать части от красного прямоугольника синим цветом»
Г) «Результат исследования занести в таблицу».
| Деятельность учителя | Деятельность учащихся |
| А) индивидуальная работа с каждым ребенком по необходимости. | а-в) Возможный ответ учеников: а) 6·8=48 клеток; б) 48:2 · 1=24 красные; в) 24: 4· 3=18 синие Анализ работ учеников.
Возможные работы детей появляются на слайде
|
| Б) коллективный анализ полученных табличных данных: 1) Чему равна часть, заштр-ная синим цветом от всего прям-ка? 2) Чему равна часть, заштр-ная синим цветом от половины прям-ка? 3) Какой вывод можно сделать сравнивая эти дроби?
|
| Часть, заштрихованная синим цветом составляет от: | | Всего прямоугольника | Половины прямоугольника | | | |
Вывод: Одно и то же число от целого составляет часть в два раза меньшую, чем от его половины. |
В целях решения задач физического и санитарно- гигиенического воспитания , развития работоспособности , профилактики утомления своевременно и качественно провести физкультминутку. Время, отведённое на организационный этап.3 минуты(слайд.).
Задание № 4.
«Дан прямоугольник размером 1 клетка на 2 клетки. Известно, что он составляет всей фигуры. Изобразить эту фигуру».
| Деятельность учителя | Деятельность учащихся |
| Вопрос наводящий: «Сколько клеток составляет целая фигура?» | Возможное решение задачи: 2:1 · 5=10 клеток составляет искомая фигура.
Анализ работ учеников.
Возможные работы детей появляются на слайде
|
Задание № 5.
«Изображено 3/7 всей фигуры. Построить всю фигуру».
| Деятельность учителя | Деятельность учащихся |
| Сколько квадратов со стороной 2 клетки вы построите? | Возможное решение: квадратов 3: 3 · 7=7всего клеток 12: 3· 7=28 клеток
Анализ работ учеников.
Возможные работы детей появляются на слайде
|
Этап информации учащихся о домашнем задании , инструктаж по его выполнению.
Дидактическая задача этапа Сообщить учащимся о домашнем задании, разъяснить методику его выполнения . Показатели выполнения дидактической задачи этапа
Усвоение следующих основных задач , входящих в содержание темы урока : умение решать задачи на применение алгоритма нахождения части от числа, алгоритма нахождения всего числа по его части.
Содержание этапа При выдаче домашнего задания учитель сообщает , кого он на следующем уроке пригласит на собеседование по всей теме , кто будет отвечать у доски , кто будет выполнять письменное задание , кто будет отвечать в режиме тихой беседы своему однокласснику, и , наконец, назначает по согласованию с учениками , кто именно будет оказывать ему помощь в домашней подготовке, при этом одного или несколько учеников он может пригласить в учебный кабинет в назначенное время.
Время ,отведённое на этап информации учащихся о домашнем задании , инструктаж по его выполнению.
2 минуты.
Задание № 6.
«Построить фигуру, если известна ее часть:
а) 7/10 всей фигуры;
б) 6/8 всей фигуры;
в) 4/9 всей фигуры;
г) 2/3 всей фигуры.
| Деятельность учителя | Деятельность учащихся |
|
| Решение: А) 7 треугольников; достроить 3 Б) 6 треугольников; достроить 2 В) 4 треугольника; достроить 5 Г) 2 равных треугольника; достроить 1. Возможные работы детей появляются на слайде
|
Подведение итогов занятия.
Дидактическая задача этапа Проанализировать , дать оценку успешности достижения цели и наметить перспективу на будущее.
Показатели выполнения дидактической задачи этапа Чёткость , лаконичность, максимум участия школьников в оценке своей работы. Осознание учениками значимости полученных результатов и готовность использовать их для достижения учебных целей.
В конце урока ученик сдаёт карточку того цвета , который соответствует его оценке урока ( фамилия на карточках не указывается) Учитель благодарит учеников за активное участие в работе на уроке.
Содержание этапа В начале урока учитель выдает ученикам карточки трёх цветов. Карточка красного цвета обозначает: «Я удовлетворён уроком, урок был полезен для меня , я много , с пользой работал на уроке, я получил заслуженную оценку, я понимал всё, о чём говорилось и что делалось на уроке».
Карточка жёлтого цвета обозначает: «Урок был интересен, и я принимал в нём активное участие, урок был в определённой степени полезен для меня , я сумел выполнить ряд заданий , мне было на уроке достаточно комфортно.»
Карточка зелёного цвета обозначает: «Пользы от урока я получил мало, я не очень понимал, о чём идет речь, мне это не очень нужно, домашнее задание я не понял, к ответу на уроке я был не готов.»
Время, отведённое на этап подведения итогов занятия 1 минута.

 Получите свидетельство
Получите свидетельство Вход
Вход




 ) Часть учеников класса осмелиться соединить заданные две точки ломанной
) Часть учеников класса осмелиться соединить заданные две точки ломанной  колько простора для творчества!
колько простора для творчества!  )
) 









 Поурочный план урока по математике «Обыкновенные дроби» (0.14 MB)
Поурочный план урока по математике «Обыкновенные дроби» (0.14 MB)
 0
0 570
570 52
52 Нравится
0
Нравится
0



