Поурочное планирование по геометрии (11 класс)

№

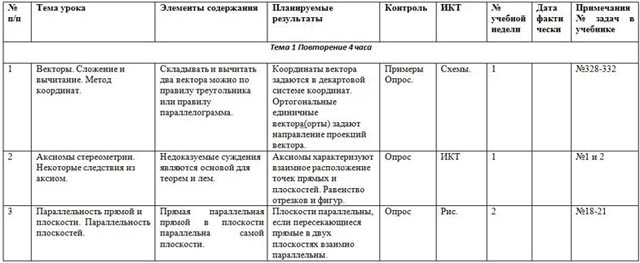
п/п

Тема урока

Элементы содержания

Планируемые результаты

Контроль

ИКТ

№ учебной недели

Дата фактически

Примечания

№ задач в учебнике

Тема 1 Повторение 4 часа

1

Векторы. Сложение и вычитание. Метод координат.

Складывать и вычитать два вектора можно по правилу треугольника или правилу параллелограмма.

Координаты вектора задаются в декартовой системе координат. Ортогональные единичные вектора(орты) задают направление проекций вектора.

Примеры Опрос.

Схемы.

1

№328-332

2

Аксиомы стереометрии. Некоторые следствия из аксиом.

Недоказуемые суждения являются основой для теорем и лем.

Аксиомы характеризуют взаимное расположение точек прямых и плоскостей. Равенство отрезков и фигур.

Опрос

ИКТ

1

№1 и 2

3

Параллельность прямой и плоскости. Параллельность плоскостей.

Прямая параллельная прямой в плоскости параллельна самой плоскости.

Плоскости параллельны, если пересекающиеся прямые в двух плоскостях взаимно параллельны.

Опрос

Рис.

2

№18-21

4

Элементы тригонометрии. Тождества. Формулы приведения. Самостоятельная работа.

Формулы приведения позволяют перейти от одной функции к другой и от тупого угла к острому.

Тождества позволяют выразить каждую тригонометрическую функцию через одну из них.

Опрос

Таблица Раздаточный материал

2

5

Теорема о перпендикулярности прямой и плоскости. Теорема о трех перпендикулярах

Прямая перпендикулярная к двум пересекающимися прямым в плоскости перпендикулярна самой плоскости.

Прямая в плоскости перпендикулярная наклонной, также перпендикулярна ее проекции в плоскости.

Опрос

Схема

3

№117-120

6

Двугранный угол. Угол между прямой и плоскостью

Наклонная и ее проекция образуют угол между наклонной и плоскостью.

Две пересекающиеся плоскости образуют двугранный угол, который равен линейному углу.

Опрос

Схема.

3

№167-171

7

Прямоугольный параллелепипед. Свойства. Призма и ее геометрические параметры.

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений.

Грани прямоугольного параллелепипеда – прямоугольники, все двугранные углы – прямые.

Опрос

Схема

4

№76-79

8

Пирамида. Геометрические параметры. Правильная пирамида.

Боковые грани пирамиды – треугольники.

Все боковые грани правильной пирамиды – равные равнобедренные треугольники.

Опрос

Схема

4

№243-246

9

Элементы симметрии правильных многогранников. Самостоятельная работа.

Различают центральную, осевую и плоскостную симметрию

Куб имеет один центр симметрии по девять осевых и плоскостных симметрий.

Примеры. Опрос

Рис.

ИКТ

5

№276-279

10

Компланарные векторы. Разложение вектора по трем некомпланарным векторам.

Три вектора компланарны, если лежат в одной плоскости.

В пространстве вектор можно разложить по трем некомпланарным векторам

Примеры. Опрос

Схема.

5

№355-358

Тема 2 Метод координат в пространстве 12 часов

11

Декартова система координат. Координаты точки. Единичный вектор.

Координаты точки в трехмерной системе определяются по осям: OX, OY, OZ

Единичные вектора: i, j, k (орты) определяют масштаб и направление осей.

Опрос

ИКТ

6

№402-407

12

Координаты пространственного вектора.

Вектор в пространстве задается его проекциями на оси координат.

Величина вектора определяется как корень из суммы квадратов его проекций

Опрос

ИКТ

6

№413-416

13

Связь между координатами вектора и координатами точки.

Координаты точки и координаты радиус-вектора совпадают.

Координаты вектора в пространстве есть разность координат конечной и начальной точек соответствующих осей.

Опрос

ИКТ

7

№416-417

14

.Задачи в координатах. Координаты середины отрезка. Самостоятельная работа.

Координаты середины отрезка равны полу сумме координат его концов по осям.

Зная координаты концов отрезка можно найти координаты середины отрезка.

Примеры

Раздаточный материал

7

№424-425

15

Расстояние между двумя точками

Зная координаты концов отрезка можно найти его длину.

Расстояние между двумя точками есть корень из суммы квадратов разностей координат этих точек по осям.

Примеры Опрос

ИКТ

8

№426-428

16

Вычисление длины вектора по его координатам.

Длина радиус-вектора равна корню из суммы квадратов его координат.

Длина любого вектора определяется как расстояние между двумя точками.

Примеры. Опрос

Схема.

8

№429-430

17

Решение задач.

Задачи в координатах.

Задачи

Раздат материал.

9

18

Контрольная работа №1

Задачи в координатах.

Раздат материал

9

19

Угол между векторами в пространстве.

Угол между векторами может быть острый, прямой и тупой.

Для сонаправленных векторов угол равен нулю, а для противоположно направленных угол равен 180 градусов.

Примеры. Опрос

ИКТ

10

№441-444

20

Скалярное произведение векторов.

Скалярное произведение векторов равно произведению их длин на косинус угла между ними

Скалярное произведение векторов используется в физике, например, для вычисления работы или магнитного потока

Опрос

ИКТ

10

№451-453

21

Вычисление угла между прямой и плоскостью.

Для вычисления угла между прямой и плоскостью используют формулу скалярного произведения.

Скалярное произведение наклонного вектора и вектора на плоскости , направленного вдоль проекции заданного вектора.

Опрос

ИКТ

11

№469=470

22

Угол между двумя прямыми. Самостоятельная работа.

Угол между двумя прямыми – это угол между направляющими векторами.

Вычисляется угол по формуле скалярного произведения.

Опрос

ИКТ

11

№464

Тема 3 Движение. 4 часа

23

Центральная симметрия

Центральная симметрия является движением

Для каждой точки изображения имеется симметричная ей точка. Центр симметрии располагается в середине отрезка, соединяющих эти две точки.

Примеры. Опрос

ИКТ

12

№479

24

Осевая симметрия.

Осевая симметрия является движением.

Для каждой точки изображения имеется симметричная ей точка относительно оси, расположенной посередине между этими точками.

12

№480

25

Зеркальная симметрия.

Зеркальная симметрия является движением.

Для каждой точки изображения имеется симметричная ей точка относительно плоскости, расположенной между этими точками посредине.

Примеры. Опрос

ИКТ

13

№482

26

Параллельный перенос. Самостоятельная работа

Параллельный перенос является движением

Точки изображения путем наложения совмещаются с новым изображением

Примеры. Опрос

ИКТ

13

№484

Тема 4 Цилиндр, конус, шар. 12 часов

27

Цилиндр. Параметры цилиндра.

Фигура вращения, полученная при вращении прямоугольника относительно любой ее стороны.

Боковая поверхность – цилиндрическая, а основания - круги

Примеры. Опрос

ИКТ

14

№525-528

28

Площадь поверхности цилиндра.

Площадь поверхности цилиндра равна площади прямоугольника, одна сторона которого – длина окружности, а вторая сторона – высота цилиндра.

Площади оснований цилиндра – площади кругов.

Примеры. Опрос

ИКТ

14

№532-534

29

Решение задач.

Задачи с цилиндром

Задачи

Раздат. материал

15

30

Конус. Параметры. Усеченный конус.

Конус – фигура вращения треугольника вокруг любой его стороны.

Усеченный конус – фигура вращения прямоугольной трапеции вокруг боковой вертикальной стороны.

Примеры. Опрос

ИКТ

15

№547-550

31

Площадь поверхности конуса.

Боковая поверхность конуса равна произведению образующей на половину длины окружности его основания.

Боковая поверхность усеченного конуса равна произведения образующей на полу сумму длин окружностей его оснований.

Примеры. Опрос.

ИКТ

16

№567-569

32

Решение задач

Задачи с конусом

Задачи

Раздат. материал

16

33

Контрольная работа №2

Задачи

Задачи

Раздат. материал

17

34

Сфера и шар. Параметры

Сфера – фигура вращения пол окружности вокруг диаметра.

Шар - фигура вращения половины круга вокруг диаметра.

Примеры Опрос

ИКТ

17

№574-576

35

Взаимное расположение сферы и плоскости.

Плоскость не касается сферы, касается и рассекает сферу.

При касании одна общая точка, при рассекании общие точки лежат на окружности

Опрос

ИКТ

18

№580-582

36

Площадь сферы.

Площадь сферы равна площади четырем больших кругов.

Большой круг есть центральное сечение шара.

Примеры. Опрос

Икт

18

№587-588

37

Решение задач.

Задачи на тела вращения

Задачи

Раздат. материал

19

38

Контрольная работа № 3

Задачи

Задачи

Раздат. материал

19

Тема 5 Объемы тел 19 часов

39

Понятие объема тел

Объем тела равен числу кубических единиц измерения.

Единицы объема – см³ , м³ и др.

Опрос

Таблица

20

№648-649

40

Объем прямоугольного параллелепипеда. Следствия.

Объем прямоугольного параллелепипеда равен произведению трех его измерений

Объем равен произведению площади основания на высоту

Примеры. Опрос

ИКТ

20

№652-653

41

Объем прямой призмы.

Объем прямой призмы равен произведению площади основания на высоту.

Основания призм – треугольники и многоугольники.

Опрос

Икт

21

№661-663

42

Объем цилиндра.

Объем цилиндра равен произведению высоты на площадь круга в основании.

Объем цилиндра равен произведению площади основания на высоту.

Примеры. Опрос

ИКТ

21

№667-669

43

Решение задач.

Задачи на объемы.

Задачи

Раздат. материал

22

44

Контрольная работа №4

Задачи на объемы.

Задачи

Раздат. материал

22

45

Вычисление объемов тел с помощью определенного интеграла.

Для вычисления объема тела под интегральной функцией является площадь сечения тела вертикальной плоскостью. Тогда пределы интегрирования соответствуют высоте тела.

Для тел вращения площади сечения круг, а для призм – прямоугольники.

Примеры. Опрос

ИКТ

23

№684-686

46

Объем наклонной призмы.

Объем наклонной призмы равен произведению площади основания на высоту

По другому, объем наклонной призмы равен произведению длины ребра на площадь сечения, перпендикулярного ребру.

Примеры. Опрос

ИКТ

23

№694-695

47

Объем пирамиды. Следствие.

Объем пирамиды равен произведению площади основания на треть высоты.

Объем усеченной пирамиды равен разности объемов полной и отсеченной пирамид.

24

№696-698

48

Решение задач.

Задачи на вычисление объема

Задачи

Раздат. материал

24

49

Контрольная работа №5

Задачи

Задачи

Раздат. материал

25

50

Объем конуса. Следствие. Самостоятельная работа.

Объем конуса равен произведению площади основания на треть высоты.

Объем усеченного конуса равен разности объемов полного и отсеченного конуса.

Примеры

ИКТ

25

№703-705

51-52

Решение задач.

Задачи на вычисление объема

Задачи

Раздат. материал

26

53

Контрольная работа №6

Задачи

Задачи

Раздат. материал

27

54

Объем шара. Объем шарового сегмента

Объем шара равен произведению площади поверхности на треть радиуса.

-

Vc = ² (R – h/3)

Опрос

ИКТ

27

№710-713, 717

55

Объем шарового слоя. Объем шарового сектора

Объем шарового слоя можно вычислить как разность двух сегментов.

Объем шарового сектора равен произведению площади поверхности шара на одну шестую высоты сегмента в секторе.

Примеры Опрос

ИКТ

28

№719-720

56

Решение задач.

Задачи на вычисление объема

Задачи

Раздат. материал

28

57

Контрольная работа №7

Задачи на вычисление объема

Задачи

Раздаточный материал

29

Тема 6 Изображение пространственных фигур 2 часа

58

Изображение фигуры на плоскости: отрезок, треугольник, параллелограмм, трапеция, окружность

Выбрав направляющую прямую пересекающей плоскость изображения, можно получить на ней проекцию изображения данной геометрической фигуры.

Так как изображения строятся с помощью параллельных прямых, то вид и форма изображения фигуры соответствует данной фигуре.

Опрос

ИКТ

29

59

Изображение пространственных фигур: тетраэдр, параллелепипед, пирамида,

Изображение пространственных фигур на плоскость отображается в виде проекций ребер данной фигуры.

Прямоугольная проекция является частным случаем параллельной проекции. Используется в черчении.

Опрос

ИКТ

30

Тема 7 Повторение 9 часов

60-66

Решение задач. Подготовка е ЕГЭ. Тесты.

Варианты заданий в сборнике ЕГЭ

Тесты. Задачи.

Сборник ЕГЭ

30-35

67-68

Итоговая контрольная работа.

Задачи

Раздаточный материал

34