Получите свидетельство
Вход
- Решение
Пусть даны отрезки PQ, MN и LK .
P
Q
N
M
L
K
Требуется построить треугольник АВС, в котором АВ= PQ , ВС= MN , СА= LK.
Проведем прямую и на ней с помощью циркуля отложим отрезок АВ, равный отрезку PQ.
А
В
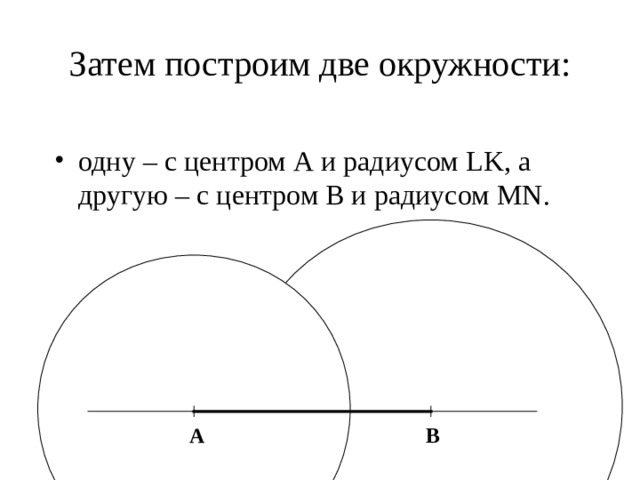
Затем построим две окружности:
- одну – с центром А и радиусом LK, а другую – с центром В и радиусом MN.
A
B
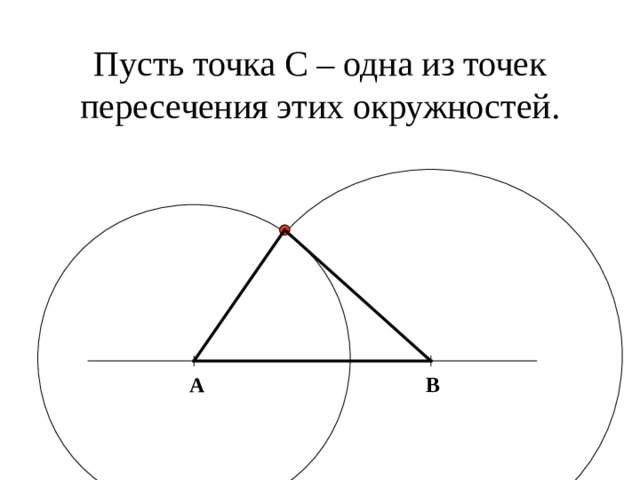
Пусть точка С – одна из точек пересечения этих окружностей.
A
B
Проведя отрезки АС и ВС, получим искомый треугольник АВС.
С
В самом деле, по построению АВ= PQ, BC=MN, AC=LK, то есть стороны треугольника АВС равны данным отрезкам.
- Задача 3 не всегда имеет решение.
- Действительно, во всяком треугольнике сумма любых двух сторон больше третьей стороны, поэтому если какой-нибудь из данных отрезков больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.
Построить треугольник по трем его сторонам. (71.5 KB)
0
832
11
Нравится
0
