ФГБОУ ВО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ М.Е.ЕВСЕВЬЕВА»
Факультет физико-математический
Кафедра информатики и вычислительной техники
РЕФЕРАТ
Построение объемных фигур и сечений в Geogebra 3D
Выполнила: Д. Ю. Трифонова, студентка 5 курса, гр. МДМ-212
Направление подготовки 44.03.05 Педагогическое образование.
Профиль Математика. Информатика
Проверила: Т. В. Кормилицына, канд. физ-мат. н., доцент
Саранск 2017
Содержание
1. Использование информационных технологий в обучении учащихся методам построения сечений многогранников
2. Программное обеспечение Geogebra 3D
3. Построение объемных фигур и сечений в Geogebra 3D
Список использованных источников
1 Использование информационных технологий в обучении учащихся методам построения сечений многогранников
Геометрия и её объекты уже в древности привлекали внимание великих умов из различных государств. Сечения геометрических пространственных фигур рассматривались в древней Греции для решения разных задач, актуальных для того времени. Свою значимость они не теряют и в наши дни.
Решение задач на построение сечений многогранников и тел вращения развивает пространственное мышление учащихся, учит их представлять фигуры в трехмерном измерении и т.д. Проблема обучения учащихся решению таких задач и формирования у них умений строить сечения многогранников разными методами особенно обострилась в последние годы в контексте подготовки выпускников школ к ЕГЭ по математике. Однако, проведенный анализ учебно-методической литературы показал, что должного внимания этой проблеме в настоящее время не уделяется. В частности, сегодня назрела необходимость выявления эффективных средств обучения учащихся методам построения сечений многогранников. В контексте современности к таким средствам с большим успехом можно отнести специализированные программные средства. Они позволяют наглядно решать проблему построения сечений многогранников как на школьном уровне обучения учащихся, так и на профессиональном уровне моделирования сечений.
2. Программное обеспечение Geogebra 3D
В выше рассмотренной задаче, может помочь программное обеспечение GeoGebra 5.0. Программа бесплатна для использования и работает на Windows XP — Windows 10.
Достоинства данной программы:
Построение кривых по заданным точкам, уравнениям, фокусам и директрисам,
Проведение операций с матрицами, комплексными числами, статистическими функциями,
Работа с таблицами и анимацией,
Позволяет создавать Java-апплеты динамических чертежей для их включения в Веб-страницы,
Переведена на 39 языков, русский включительно
Представляет собой симбиоз нескольких научных сфер.
Имеет версии работающие на Android, Linux и MacOS X.
Программа имеет широкое применение в образовании, расширяет границы изучаемой области во всех разделах математического и геометрического курса. Позволяет работать с математическими объектами как на плоскости, так и в пространстве.
3. Построение объемных фигур и сечений в Geogebra 3D
Продемонстрируем решение задач на построение сечения многогранника с помощью программного обеспечения GeoGebra.
Рассмотрим задачу базового уровня.
Дан прямоугольный параллелепипед ABCDEFGH. Построим сечение плоскостью, проходящей через точки I, J и K (Рис. 1).
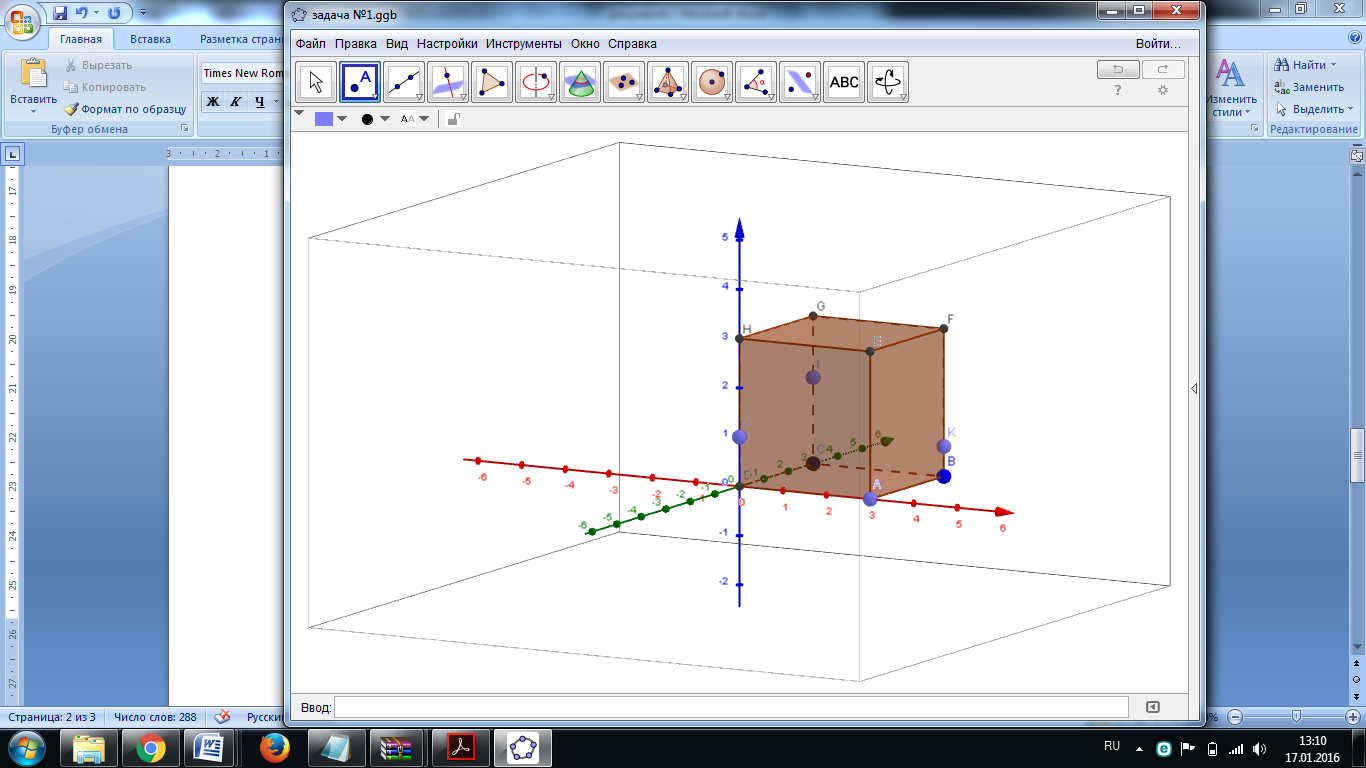
Рис. 1
Соединим точки, которые лежат на одной грани, а именно: I и K, J и I. Проведем через точку J прямую, параллельную прямой IK и полученную точку пересечения назовем L (Рис. 2).
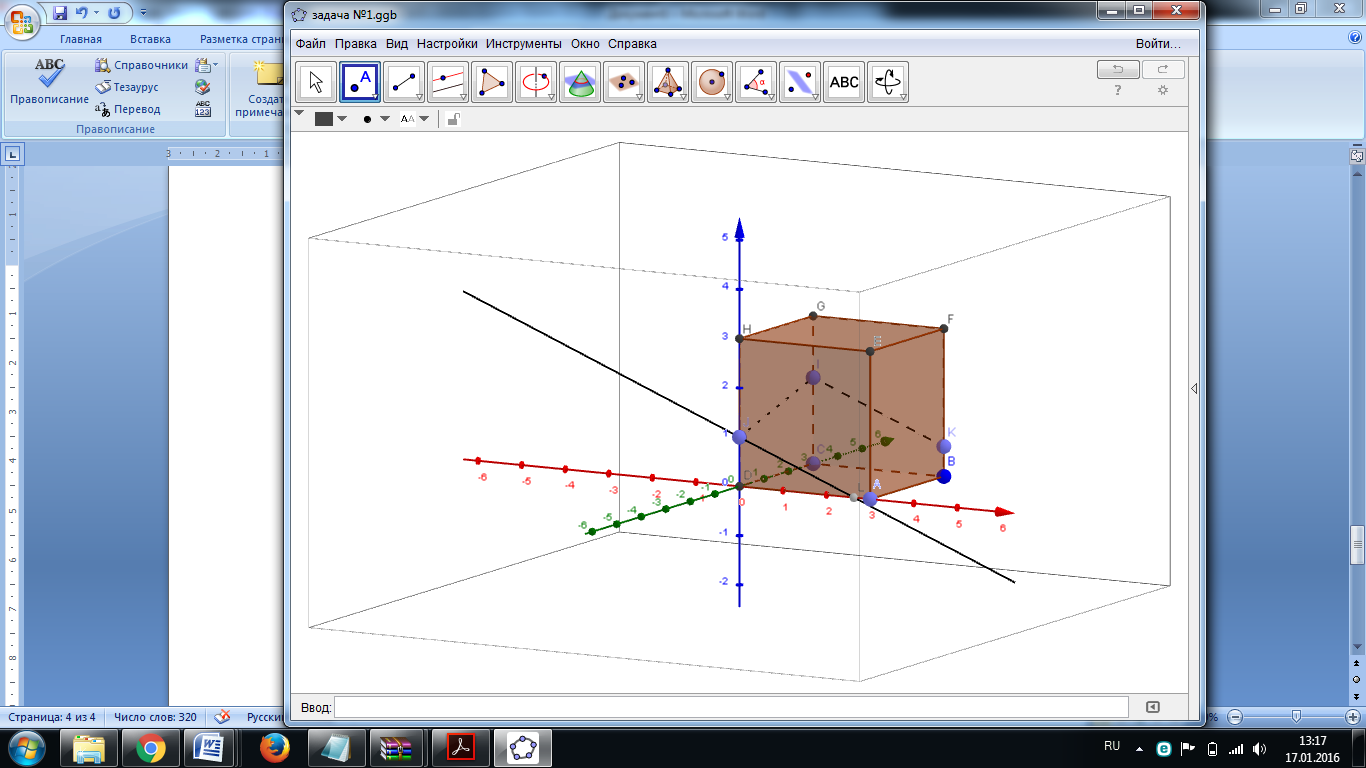
Рис. 2
Проведем через точку K прямую, параллельную прямой IJ и полученную точку пересечения назовем M. Соединим точки, лежащие на одной грани L и M (Рис. 3).
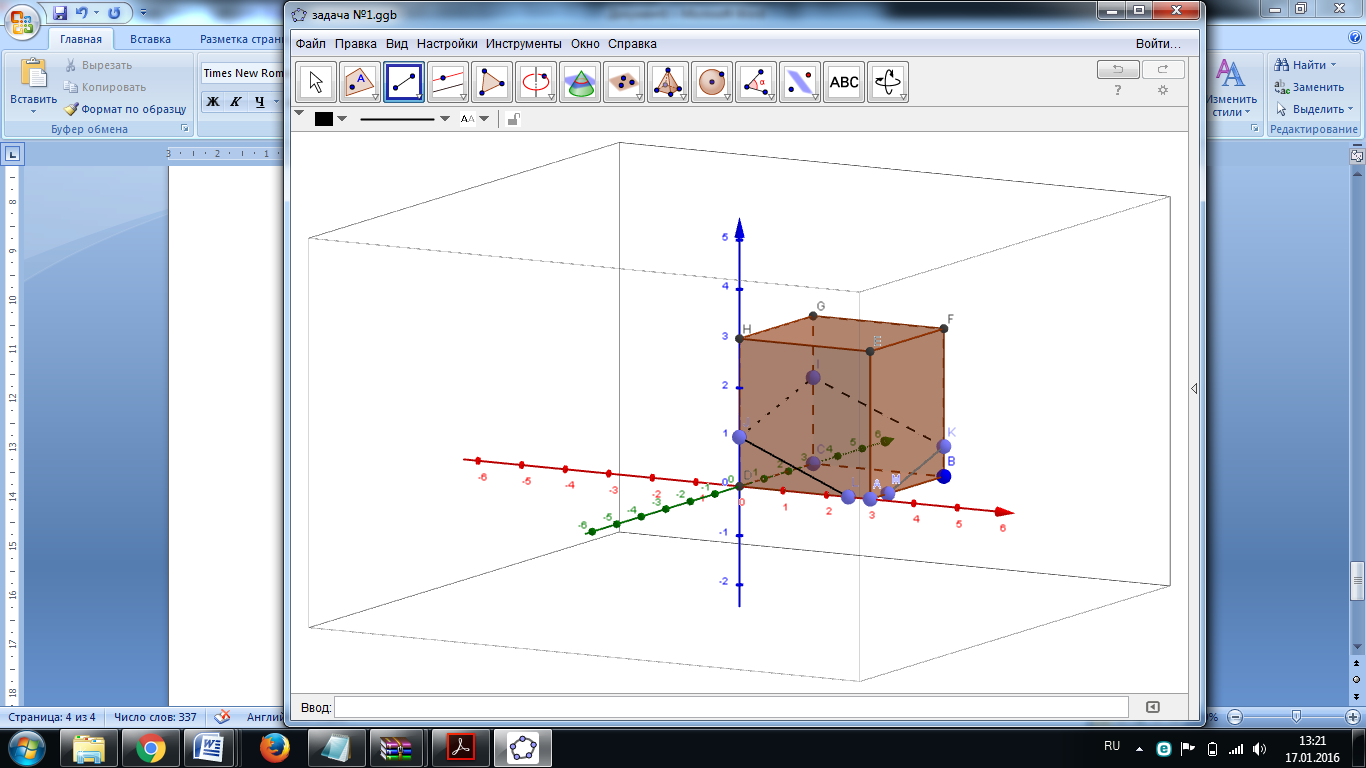
Рис. 3
Полученная фигура и будет представляет собой сечение куба (Рис. 4).
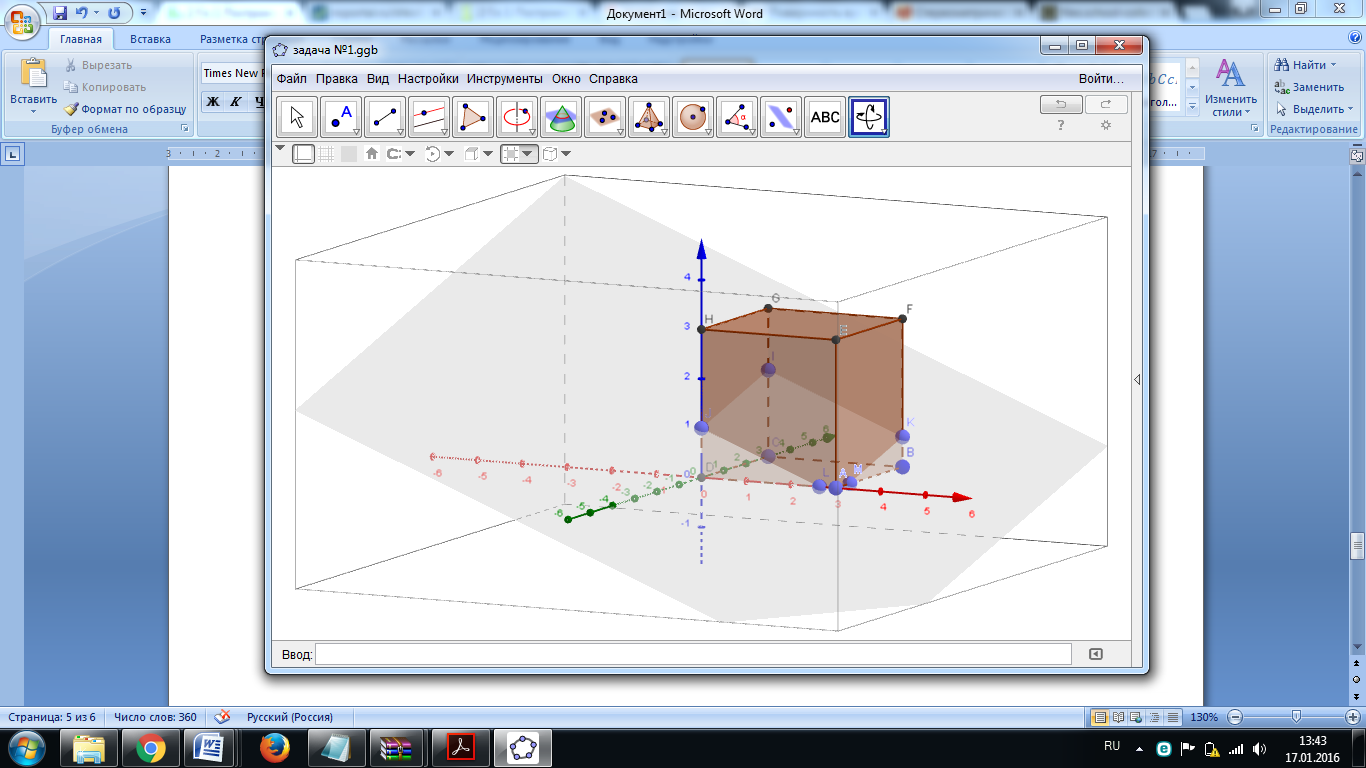
Рис. 4
Рассмотрим задачу повышенного уровня сложности.
Существует ли сечение куба, являющееся правильным шестиугольником?
Попробуем выяснить это с помощью программы математического моделирования, вдобавок рассмотрим основные принципы работы с программой. Создаем 3D полотно и строим куб. Слева в окне Панель объектов можем наблюдать такие данные, как объем, длины ребер, координаты вершин, площади граней. Для наглядности, делаем грани прозрачными. Для того, чтобы решить эту задачу нам придется задействовать пространственное мышление и представить, как бы располагался многоугольник сечения, если бы такой существовал. В Гео гебра есть такая возможность, как построение плоскости по трем точкам. Обозначаем точками пересечения плоскости и ребер куба, соединяем их многоугольником. Очевидно, что шестиугольник мы вписать можем, остаётся проверить его правильность, которая заключается в равенстве сторон. Можно заметить, что каждая сторона шестиугольника является стороной квадрата вписанного в грань куба, которые будут равны. Следовательно многоугольник, образованный сечением куба является правильным шестиугольником.
С методической точки зрения, в Гео гебре есть такая интересная возможность, как "шаги построения", которая позволяет проиграть действия в программе с нужной скоростью.
Развитие информационных технологий требует прогрессивного подхода в работе различных сфер деятельности человека. Поэтому развитие пространственного мышления играет немало важную роль в современном обществе. Так как каждое новое поколение требует увеличения интеллектуального развития общества. Представление пространственных объектов с помощью программ визуализации так же является неотъемлемым шагом в современном прогрессе.
Список использованных источников
Новожилова, С. А. Многогранники / С. А. Новожилова. – Иваново: Ивановский государственный архитектурно-строительный университет, ЭБС АСВ, 2005. – 41 c.
Черняева А. Р. Задачи на построение сечений многогранников как средство развития пространственного мышления в курсе геометрии: метод. пособие. – Омск: Изд-во ОмГПУ, 2003. – 48 с.
Корянов, А. Г. Математика. ЕГЭ 2011 (типовые задания С2). Многогранники: виды задач и методы их решения / А. Г. Корянов, А. А. Прокофьев, 2001. – 89 с.
Темербекова, А. А. Информационные технологии в физико-математическом образовании: учебно-методический комплекс / А. А. Темербекова. – Горно-Алтайск: изд-во ГАГУ, 2010. – 83 с.
Далингер В. А. Избранные вопросы информатизации школьного математического образования / В. А. Далингер. – М.: Флинта, 2011. – 150 с.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Построение объемных фигур и сечений в Geogebra 3D (775.59 KB)
Построение объемных фигур и сечений в Geogebra 3D (775.59 KB)
 0
0 1050
1050 12
12 Нравится
0
Нравится
0


