Тема: Понятие вектора. Откладывание вектора от данной точки.
Место урока в теме: первый урок в теме «Векторы»
Форма урока: комбинированный.
Цель урока: Создать условия для более глубокого и качественного усвоения учащимися темы: «Векторы»
Задачи: 1)Ознакомить учащихся с простейшими понятиями: вектора, его начала и конца, нулевого вектора, длины вектора, коллинеарных, сонаправленных, противоположно направленных, равных векторов. Научить откладывать вектор, равный данному.
2)Обеспечить развитие конструкторско-практической деятельности учащихся, направленной на формирование наглядно-образного мышления, внимания, воображения и творчества.
3)Отработать в интерактивном режиме элементарных базовых умений и тем самым повысить уровень возможностей учащихся в овладении умениями комплексного характера при изучение темы «Векторы».
4)Воспитать в учениках целеустремлённость в достижении положительного результата и прочного познавательного интереса к математике.
Ожидаемый результат: Сформировать у учащихся прочные знания, умения и навыки по основным понятиям темы «Векторы»
Ход урока:
I. Организационный момент: подготовка рабочего места учащегося, установка ЦОР «Открытая математика. Планиметрия» на ученические ПК и в проектор с выводом изображения на экран.
II.Мотивация целей урока: Понятие вектора и действия над векторами вводятся так, как это принято в физике, а именно, как «величины, характеризующиеся не только числовым значением, но и направлением». Геометрический вектор – это направленный отрезок. Необходимо обратить внимание, что многие задачи проще решаются, если в них использовать векторный метод решения. А для более глубокого понимания векторов и операций над ними полезно воспользоваться знаниями о векторных величинах, полученных на уроках физики. Кроме этого ваша работа сегодня будет связана с компьютерами, а я знаю, что вы это любите. Но чтобы не навредить своему здоровью, нам необходимо вспомнить технику безопасности. (Проходим инструктаж по технике безопасности)
III. Математический диктант:
На окружности последовательно взяты точки A, B, C, D. Является ли четырехугольник ABCD выпуклым?
Высота параллелограмма образует с его стороной угол 17°. Найти наименьший угол параллелограмма.
Периметр параллелограмма больше одной стороны на 29 см и больше другой стороны на 22 см. Найти наименьшую сторону параллелограмма.
Основания равнобедренной трапеции равны 10 и 30, а острый угол – 60°. Найти периметр трапеции.
Высота ромба в 8 раз меньше его периметра. Найти наименьший угол ромба.
IV.Новая тема:
1. Ввести понятие вектора
2. Изображение и обозначение вектора.
3. Ввести понятие нулевого вектора, длины вектора и равных векторов.
4. Коллинеарные векторы: сонаправленные и противоположно направленные.
5. Свойства равенства векторов.
6. Откладывание вектора от произвольной точки, равного данному.
(В ходе изучения темы можно использовать ЦОР: «Открытая математика. Планиметрия» открыв его в разделе теоретического материала: Глава 11 Векторы. Демонстрируем через проектор, останавливая в тех местах где требуются записи в тетрадь)
11.1. Основные понятия и свойства 
Вектором называется направленный отрезок. Если у отрезка AB его концы равноправны, то для вектора один из концов отрезка, например, A называется началом, а другой, то есть B, – концом. Обозначим вектор либо указанием концов отрезка, причем начало вектора ставится на первое место, либо строчной латинской буквой со стрелкой или чертой над буквами.
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100101.swf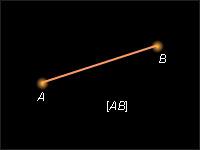 ../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100101.jpg
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100101.jpg
1
Рисунок 11.1.1.
Отрезок AB
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100102.swf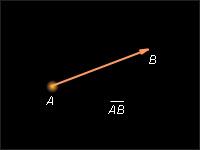 ../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100102.jpg
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100102.jpg
2
Рисунок 11.1.2.
Вектор 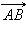
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100103.swf ../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100103.jpg
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100103.jpg
3
Рисунок 11.1.3.
Вектор 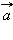
На рис. 11.1.1 изображен обычный отрезок AB, а на рис. 11.1.2 – вектор 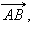 на рис. 11.1.3 – вектор
на рис. 11.1.3 – вектор 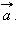
Векторы 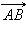 и
и 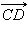 называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы
называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы 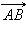 и
и 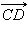 называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100104.swf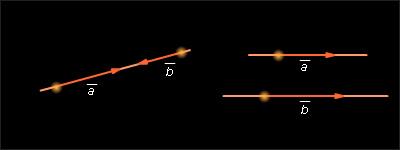 ../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100104.jpg
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100104.jpg
4
Рисунок 11.1.4.
Коллинеарные векторы
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора 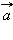 обозначим
обозначим 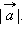 Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине. На рис. 11.1.5 вектор
Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине. На рис. 11.1.5 вектор 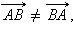 а вектор
а вектор 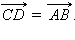
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100105.swf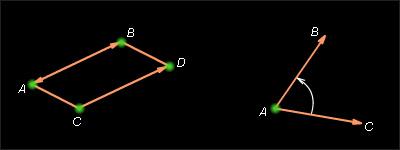 ../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100105.jpg
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100105.jpg
5
Рисунок 11.1.5.
Равенство векторов
Нулевым вектором 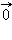 называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. Вектор называется единичным, если его абсолютная величина равна единице.
называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. Вектор называется единичным, если его абсолютная величина равна единице.
Замечание 11.1Любую пару векторов, один из которых равен нулевому вектору будем считать коллинеарными.
Свойства равенства векторов:
каждый вектор равен самому себе;
если вектор 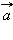 равен вектору
равен вектору 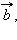 то
то 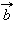 равен
равен 
два вектора, равные третьему, равны.
V. Закрепление:
1. Работа в рабочих тетрадях: решить устно задачу №112 (стр. 53, из рабочей тетради для 8 класса)
Задача №112
Ответы:
А) ВА, ВС, ВD
Б) ВА, DА
В) вектор с началом и концом в точке С называется нулевым и обозначается СС или 0
Г) |ВС| =4, |ВD|=4
Д) вектору ВА коллинеарен вектор СD
2.Даны чертёжи. (из задач с решениями ЦОР: «Открытая математика. Планиметрия»)
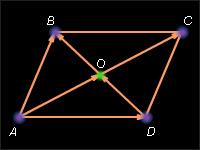
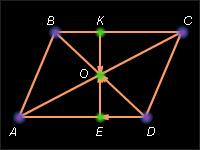
Ответить на вопросы:
А) Укажите на рисунке сонапрвленные, противоположно направленные, равные вектора;
Б) Укажите на рисунке векторы, длины которых равны. Равны ли при этом сами векторы?
VI.Самостоятельная работа (обучающегося характера): Для проверки знаний которые вы получили на этом уроке проведём ещё один тест на ПК. ЦОР: «Открытая математика. Планиметрия»
I – вариант.
1. Перечертите рисунок в тетрадь. Постройте векторы МР и NQ, такие, что МР = а, NQ противоположно направленный с а
2. АВСD – параллелограмм. Докажите, что АВ = DС
II – вариант.
1. Перечертите рисунок в тетрадь. Постройте векторы АВ и СD, такие, что СD = m, АВ противоположно направленный с m
2. Точки M, N, K, P не лежат на одной прямой и векторы KM = PN Докажите, что KMNP – параллелограмм.
III – вариант (для более подготовленных учащихся)
1.Точка M лежит на отрезке АВ. Постройте векторы MK и MN, такие, что MK=AB, MN=BA.
2. Точка О лежит внутри четырёхугольника АВСD, АО=ОС,ВО=ОD. Докажите, что АВ=CD.
VII. Рефлексия: И так давайте подведём итоги: что нового вы сегодня узнали, чему научились? (Следуют ответы учащихся)
В результате мы должны знать определения вектора и равных векторов, уметь изображать и обозначать векторы, откладывать от данной точки вектор, равный данному.
VIII. Домашнее задание: Вопрос 6 (стр. 204) задачи 743, 747, 748.


 Получите свидетельство
Получите свидетельство Вход
Вход



 ../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100101.jpg
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100101.jpg ../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100102.jpg
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100102.jpg ../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100104.jpg
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100104.jpg ../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100105.jpg
../../../Program Files/Physicon/Open Math 2.6. Planimetry/content/chapter11/section/paragraph1/images/1100105.jpg










 Понятие вектора. Откладывание вектора от данной точки (разработка урока) (80.79 КB)
Понятие вектора. Откладывание вектора от данной точки (разработка урока) (80.79 КB)
 0
0 1567
1567 231
231 Нравится
0
Нравится
0


