Урок по теме « Теорема Виета» 8 класс.
Тип урока : комбинированный.
План урока.
Структура урока.
I. Актуализация знаний.
1.2. Фронтальная опрос, с целью актуализации знаний.
1.3. Решение проблемной задачи с целью мотивации применения.
II. Формирование новых знаний и способов действия.
2.1 Выполнение задания исследовательского характера с целью активизировать учебно -познавательную деятельность учащихся и повысить интерес к предмету.
2.2. Фронтальная работа с целью получения определения теоремы виета.
2.3. Беседа с классом с целью доказательства теоремы.
III. Применение знаний, формирование умений и навыков.
3.1. Решение мотивационной задачи и задач по готовым чертежам с целью закрепления теоремы.
3.2. Решение задач, с целью применения доказанной теоремы.
3.3.Решение задач с целью первичного закрепления изученного материала.
3.4. Итог урока. Рефлексия. Домашнее задание
Задачи:
Способствовать развитию умений учащихся обобщать полученные знания, проводить анализ, синтез, сравнения, делать необходимые
выводы; содействовать развитию умений применять полученные знания в типовых и нестандартных условиях; обеспечить условия для
развития умений грамотно, четко и точно выражать свои мысли; создать условия, в которых учащиеся могли бы самостоятельно
планировать и анализировать собственные действия, реально оценивать свои возможности и знания, способствовать развитию памяти,
внимания.
Воспитательные:
Учебные
1. Повторить решение квадратных уравнений с использованием методов, знакомых учащимся.
2. Познакомить с теоремой Виета и ей обратной.
3. Научить применять теорему для приведенных квадратных уравнений на практике.
Развивающие
1. Развивать такие метапредметные универсальные учебные действия (УУД) как анализ, синтез, обобщение, сравнение, классификация в процессе решения проблемной ситуации
2. Развивать навыки самостоятельной деятельности учащихся для достижения образовательных целей урока.
3. Развивать умение конструктивно взаимодействовать в паре, в группе в целях решения учебных задач.
Воспитательные
1. Формировать коммуникативные качества личности учащегося для конструктивного взаимодействия с учителем и партнёрами в группе в целях решения учебных задач.
2. Прививать интерес к математике как науке.
Предметные
1. В результате самостоятельного исследования и анализа учебного материала учащиеся смогут:
а) установить закономерные связи между корнями и коэффициентами квадратного уравнения;
б) самостоятельно сформулировать идеи, заложенные в основу теоремы Виета, а также ей обратной теоремы;
в) применять новое знание на практике при решении уравнений и задач (нахождение суммы и произведения корней приведенного квадратного уравнения, определение знаков корней уравнения, решение квадратных уравнений, проверке правильности нахождения корней квадратных уравнений).
2. Освоить применение метода QR-кода для осуществления самоконтроля при решении уравнение
Метапредметные
В результате сотрудничества с учителем и взаимодействия в паре и группе учащиеся научатсяставить учебные цели и использовать приемы умственной деятельности, такие как анализ, классификация, обобщение и подведение под понятие, для достижения планируемых результатов урока.
Личностные
Результатом использования учителем деятельностного подхода к освоению новых знаний, а также метода самоконтроля через QR-код ожидается повышение самооценки личности учащегося и повышение мотивации к дальнейшему изучению математики.
Проверяется наличие домашнего задания. К тем номерам , которые вызвали затруднения дать пояснения на уроке.
Устная работа:
В ходе устной работы определить на сколько хорошо учащиеся владеют основными понятиями о квадратных уравнениях, какие пробелы есть в знаниях?
Фронтальный опрос
Дайте определение полных, неполных и приведенных квадратных уравнений.
Назовите полные, неполные и приведенные квадратные уравнения:
3х2 – 2х = 0 -21х2 + 16х=0
7х2 – 16х + 4 =0 х2=0
Х2 – 3 = 0 х2 + 4х + 4 =0
- х2 +2х - 4 =0 х2=4
Преобразуйте квадратное уравнение в приведенное:
3х2 + 6х – 12 =0 0,2х2 + 0,5х – 2 =0
-х2 – 2х + 16 = 0 -5х2 + 10х -2 =0
4. От чего зависит наличие или отсутствие корней квадратного уравнения?
5. По какой формуле находятся корни квадратного уравнения?
4) «Открытие» теоремы Виета.
Организовываем исследовательскую деятельность, что позволяет активизировать учебно -познавательную деятельность учащихся и повысить интерес к предмету.
Для этого разбиваем класс на пять групп, каждой из которых дается задание решить приведенное уравнение. После его решения один представитель от каждой группы выходит к доске и заполняет соответствующую строку в таблице:
| Уравнение | b
| c
| Корни
| Сумма корней | Произведение корней |
| Х2 +11х -12 = 0
|
|
|
|
|
|
| Х2 – 6х – 7 = 0
|
|
|
|
|
|
| Х2 + 3х – 10 = 0
|
|
|
|
|
|
| Х2+ 5х + 6 = 0
|
|
|
|
|
|
| Х2– х – 12 = 0
|
|
|
|
|
|
После этого учитель предлагает учащимся сравнить сумму и произведение полученных корней с коэффициентами b и c и выдвинуть гипотезу. Учитель подтверждает сделанное предположение, сообщая, что данное утверждение называется теоремой Виета, обращая внимание учащихся, что эта теорема справедлива для приведенных квадратных уравнений.
Краткий исторический материал:
Француа Виет – французский математик, ввел систему алгебраических символов, разработал основы элементарной алгебры. Он был одним из первых кто стал обозначать числа буквами, что существенно развило теорию уравнений.
Рассмотреть доказательство теоремы можно по учебнику (с. 127– 128), привлекая учащихся, поскольку оно не является сложным. После доказательства на доску выносится запись:
В этом уроке мы «откроем» зависимость между корнями и коэффициентами приведенного квадратного уравнения. Сформулируем теорему Виета. Докажем ее. Рассмотрим применение теоремы Виета на практике.
Решим уравнение: ![]() .
.
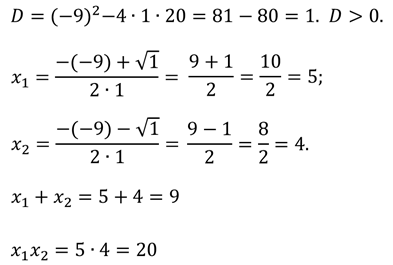
Если внимательно посмотреть на коэффициенты этого квадратного уравнения, то можно увидеть, что сумма корней, которую нашли, равна второму коэффициенту. Правда, только взятому с противоположным знаком. А произведение этих корней равно свободному члену. Так вот таким свойством обладает любое приведенное квадратное уравнение.
Теорема: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
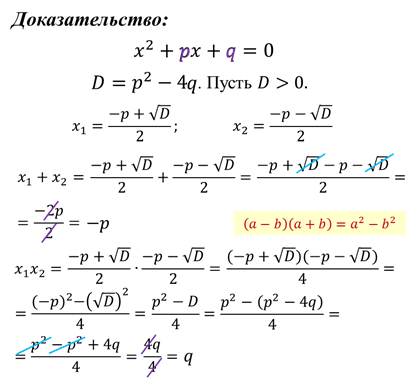
Т.е. мы с вами показали, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение этих же корней равно свободному члену уравнения. Значит, теорема доказана.
При дискриминанте равном нулю квадратное уравнение имеет один корень. Но если считать, что когда дискриминант равен нулю, уравнение имеет два равных корня, то теорема будет верна и в этом случае. Это следует из того, что при дискриминанте равном нулю корни уравнения также можно найти по формуле:
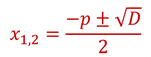
Теорему, которую доказали, называют теоремой Виета. Соотношения корней впервые обнаружил французский математик Франсуа Виет.

Франсуа Виет внёс большой вклад в развитие математики. По существу он создал новую алгебру. Виет ввёл в неё буквенную символику и показал, как, оперируя символами, можно получить результат, который применим к любым соответствующим величинам, т.е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление. Так, в частности, он предложил использовать буквы для обозначения коэффициентов. Самым важным своим открытием Виет считал установление связи между координатами и коэффициентами уравнений.
Пусть квадратное уравнение ![]() имеет корни
имеет корни ![]() и
и ![]() . Равносильное ему приведенное квадратное уравнение имеет вид:
. Равносильное ему приведенное квадратное уравнение имеет вид:
![]()
И, следовательно, имеет те же корни.

С помощью теоремы Виета можно решать многие квадратные уравнения устно, не пользуясь громоздкими формулами корней.
Задание 1: не решая уравнения, найти сумму и произведение корней, если они существуют.
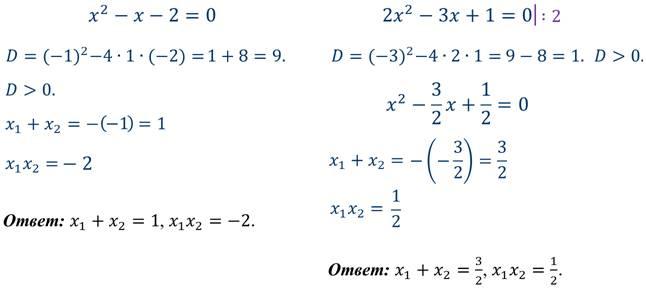
Задание 2: найти подбором корни уравнения.
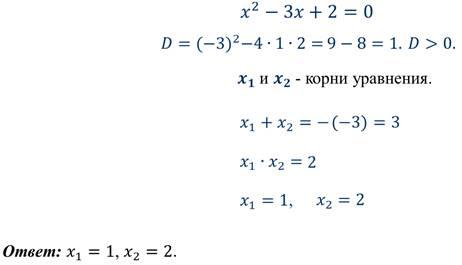
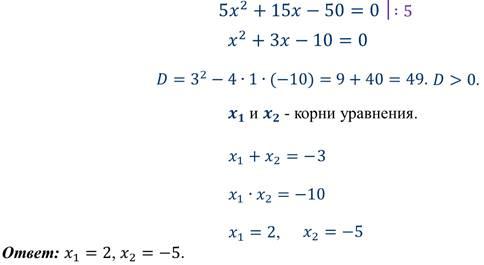
Итоги:
На этом уроке познакомились с теоремой Виета, которая имеет следующую формулировку: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
При выполнении этого задания необходимо предотвратить формальное применение теоремы Виета. Нужно убедиться, что квадратное уравнение имеет корни. Если учащиеся сами не выскажут эту мысль, то при решении третьего задания предложить им найти дискриминант уравнения и сделать соответствующий вывод.
Далее рассматривается вывод корней неприведенного квадратного уравнения.
При выполнении устной работы в начале урока учащиеся вспомнили, как преобразовать квадратное уравнение в приведённое. Следует предложить им самостоятельно вывести формулы для неприведённого квадратного уравнения, используя теорему Виета.
Выучив теорему Виета , вы тоже разрешите для себя уйму всяких проблем.
На данном этапе учитель на доске показывает решение приведенного квадратного уравнения с использованием теоремы Виета. Акцентирует внимание учащихся на перебор корней, знаки, быстроту решения.
№ 583
х2-9х + 20=0 Д0
х1х2=20=4* 5= -4 * (-5)= 2 * 10= -2 * (-10) = 1*20=-1 * (-20)
из этих множителей выбираем х1=4 , х2= 5 так как х1 + х2= 9.
Учащиеся выполняют на доске №583, №587, №588.
Все допущенные ошибки разбираются всем классом.
№ 589 разбирается учителем на доске.
Устно:
Составьте квадратное уравнение, имеющее следующие корни:
| X1 | X2 | X1• X2 | X1+X2 | Уравнение |
| 2 | 5 |
|
|
|
| 2 |
| 0,8 |
|
|
|
|
| 8 | -6 |
|
|
|
| 8 | 6 |
|
| 4 | -3 |
|
|
|
| 12 | 0,5 |
|
|
|
|
|
|
|
|
|
Мы с вами уже знаем теорему Виета. Вспомним её формулировку: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Справедлива также теорема обратная теореме Виета. Запишем её формулировку. Если числа ![]() и
и ![]() таковы, что их
таковы, что их ![]() , а
, а ![]() , то эти числа являются корнями квадратного уравнения
, то эти числа являются корнями квадратного уравнения ![]() .
.

С помощью обратной теоремы Виета удобно проверять, правильно ли найдены корни квадратного уравнения, а также по указанным корням составлять уравнения.
Задание: найдите корни уравнения и выполните проверку по теореме, обратной теореме Виета.
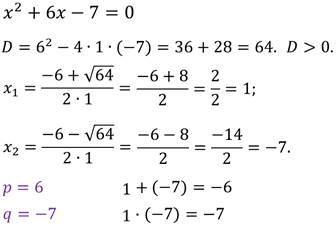
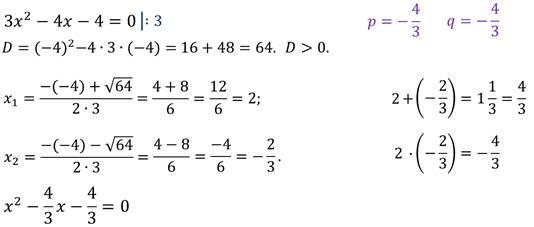
И выполним обратное задание: составьте квадратное уравнение по его корням.
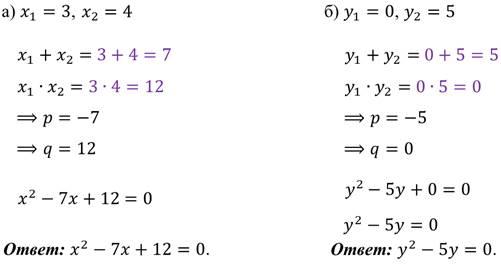

Задание: один из корней уравнения ![]() равен четырем. Найдите другой корень и коэффициент
равен четырем. Найдите другой корень и коэффициент ![]() .
.
Решение:
Задание: один из корней уравнения равен минус пяти. Найдите другой корень и коэффициент
.
Итоги:
Сегодня на уроке мы познакомились с обратной теоремой Виета, которая имеет следующую формулировку: если числа ![]() и
и ![]() таковы, что их сумма равна
таковы, что их сумма равна , а произведение равно
, то эти числа являются корнями квадратного уравнения
![]() .
.
- урок заставляет задуматься;
- урок был обычен;
- урок был интересен.
8) Домашнее задание по двум уровням сложности. Ученики самостоятельно выбирают уровень сложности домашнего задания. Но учащимся претендующим на оценки «4» и «5» рекомендуется выбрать домашнее задание второго уровня сложности. По желанию учащихся предлагается написать доклад «Француа Виет»
I №584, 585,541 (е,ж)
II № 582, 587,591
Подведение итогов занятия:
На данном этапе дается анализ и оценка успешности достигнутых целей урока. По результатам урока выставляются оценки. Намечаются перспективы последующей работы.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Полный конспект :теорема виета (406.5 KB)
Полный конспект :теорема виета (406.5 KB)
 0
0 1328
1328 53
53 Нравится
0
Нравится
0


