Полный конспект применения подобия к док-ву теорем

Тип урока: комбинированный.

Цели урока: обучающие):

формировать умения:

• применять признаки подобия треугольников для решения задач,

• решать задачи по готовым чертежам;

• распознавать подобные треугольники,

• делать вывод о равенстве углов и пропорциональности сторон.

развивающие:

развивать:

• умение анализировать,

• подведение под понятие

• обобщать изучаемые факты,

• творческие способности,

• пространственное воображение и логическое мышление учащихся;

• познавательную активность.

Воспитательные:

воспитывать:

• аккуратность и прилежание;

• навыки самоконтроля;

• навыки коллективного труда.

Планируемые результаты:

Метапредметные: формирование у учащихся умения мыслить логически, рассуждать; формировать умения построения речевого высказывания.

Предметные: применять признаки подобия треугольников при решении задач и док-ве теорем.

Личностные: положительная учебная мотивация; развивать интерес к предмету; воспитывать самостоятельность и аккуратность; воспитывать самоуважение и уважение к окружающим людям.
Тема предыдущего урока Контрольная работа № 3 по теме: «Признаки подобия треугольников»

Тема следующего урока: Средняя линия треугольника (решение задач)

Домашнее задание к уроку: №561 (Докажите, что два равносторонних треугольника подобны)

Структура урока. 
I. Актуализация знаний.
1.1. Орг.момент (2 мин). 

1.2. Анализ ошибок контрольной работы, сообщение оценок, обсуждение задач, с которыми не справились большинство, надом-работа над ошибками. (3минуты)
1.3. Фронтальная опрос, с целью актуализации знаний (5 мин). 
1.4. Решение проблемной задачи с целью мотивации применения подобия треугольников при доказательстве теорем, постановка цели урока.( 7 мин).

II. Формирование новых знаний и способов действия. 
2.1. Фронтальная работа с целью получения определения средней линии треугольника, ее свойств.(4)

2.3. Беседа с классом с целью доказательства теоремы.(6 мин)
III. Применение знаний, формирование умений и навыков. 

3.1. Решение мотивационной задачи и задач по готовым чертежам с целью закрепления теоремы.

3.2. Решение задачи о медианах, с целью применения доказанной теоремы.
3.3.Решение задач с целью первичного закрепления изученного материала.( 7 мин)
3.4. Итог урока. Рефлексия. Домашнее задание ( 3 мин).

Ход урока

1.3. Для работы на уроке нам необходимо  повторить определение подобия и признаки подобия треугольников. Давайте сделаем это. Ребята, я попрошу вас продолжить утверждения:

«Два треугольника называется подобными, если …».

Ответ.  Их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

«Если три стороны одного треугольника ….».

Ответ. Пропорциональны трем сторонам другого, то такие треугольники подобны. (Это третий  признак подобия треугольника).

«Если два угла одного треугольника …».

Ответ.  Соответственно равны двум углам другого, то такие треугольники подобны. (Это первый признак подобия треугольников по двум углам).

А кто сможет сформулировать второй признак подобия треугольников?

Ответ. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны..

Далее, вы видите на доске пары треугольников, нужно определить подобны ли они, если да, то почему?

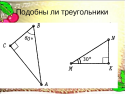
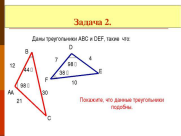
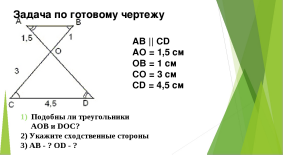
Даны два подобных треугольника, найти х и у. 

Ответ. Треугольники ДАВС и ДА1В1С1  подобны (по условию), воспользуемся третьим признаком подобия треугольников:

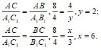
Ответ: х=6, у=2.

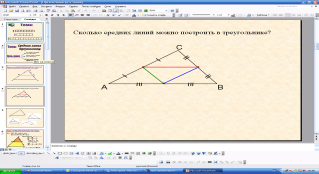
1.4. Давайте решим с вами такие легкие задачи:

1.Работа с чертежами, которые изображены на рисунке.

-Чему равен угол АВМ на 1 чертеже?(23 градуса).

Почему?(Так как по условию дано что ВМ- биссектриса, значит она делит угол В пополам).

-Чему равна сторонаSL на 2 чертеже?(так как на чертеже указано что стороны SL иRL равны следовательно сторона SL =2,7см).

-Следовательно, FL чем является в треугольнике? (медианой).

-На третьем чертеже МN чему равна?(дети затрудняются ответить).

-Мы не можем с вами сразу ответить на вопрос. Что для этого нужно знать? (надо узнать ,что это за прямая и как ее можно найти).

Сегодня мы с вами познакомимся с определением и свойствами этой прямой, узнаем чему она равна в треугольнике, и в конце урока ответим на вопрос нашей задачи, которую мы сейчас не смогли решить.

2.1. Практическая работа. Введение определения средней линии треугольника.

Практическая работа.

Постройте любой треугольник ABC.

а) Отметьте M и N – середины сторон AB и BC.

Б)Соедините отрезком.

В)Дайте «имя» отрезку MN, исходя из построения.

Г) попробуйте дать определение

-Давайте посмотрим на чертеж нашей задачи.

Где находится отрезок, который нам надо найти? (в середине треугольника)

Что нам дано по чертежу? ( отрезок АМ=МВ, СN=NB).

-Следовательно, что делает отрезок MN со сторонами треугольника? (делит стороны пополам).

Где лежат точки отрезка MN?(на серединах сторон треугольника). Какой вывод можем сделать?(МN- отрезок, соединяющий середины двух сторон треугольника).

-Отсюда идет названия отрезка –MN-называется средней линией треугольника.

3.Запись в тетрадях определения средней линии и чертеж задачи.

Определение: Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника.

В тетрадях рисунок и запись: Если АМ = МВ и СN = NВ, то МN- средняя линия треугольника

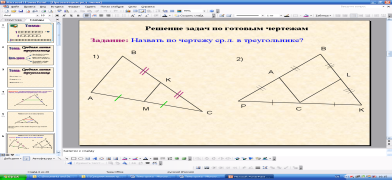
4.Работа по готовым чертежам (отработать умение распознавать на чертежах ср. л. треугольника)

-Сколько средних линий можно построить в треугольнике? Почему?(3 средние линии, потому что в треугольнике 3 стороны)

-Назовите по чертежу ср. л. в треугольнике?(KM; CA; CL)

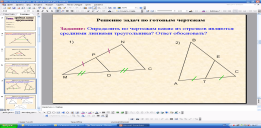
-Определите по чертежам, какие из отрезков являются средними линиями треугольника? Ответ обосновать.(PD,так как концы отрезка соединяют середины сторон треугольника; EF,так как делит делит стороны треугольника пополам(на равные отрезки)).

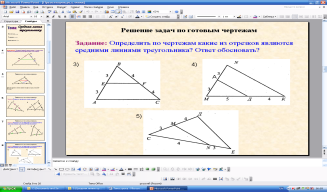
3.Построение чертежа и краткая запись содержания теоремы.

Свойство ср. л. треугольника. Продолжим изучение нового материала. Работаем ребята с тем же чертежом. Проведем эксперимент, с помощью линейки, угольников по рядам:

-Что значит выяснить взаимное расположение прямых?(прямые пересекаются, не пересекаются).

-Что мы можем сказать о прямых МN и АС?(они не пересеаются, значит МN II АС)

-Сравните длины отрезков МN и АС.Что можно сказать о их длинах?(MN в 2 раза меньше АС)

Вот мы ребята и вывели основное свойство о ср. л. треугольника.

Может быть кто-то попробует сформулировать свойство о ср. л. треугольника.

Теорема. 
Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине

Построение чертежа в тетрадях и краткая запись содержания теоремы учащимися.

Дано: АВС

МN-средняя линия

Доказать: MN АC

MN=AC

4.Поиск доказательства, доказательство и его запись.

Рассмотрим треугольник АВС. МN-средняя линия этого трегольника.Докажем ,что MN АC,и MN=AC.

-Ск треугольников мы видем на чертеже? Назовите их.(АВС и MBN).

-Что мы можем о них сказать? Что мы видим?(угол В-общий;средняя линия разделила стороны пополам, следовательно сторона МВ в 2 раза меньше стороны АВ,а BN в 2 раза меньше стороны ВС, следовательно 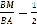 ;  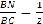,следовательно треугольники подобны по 2 признаку),

Тогда как относиться сторона MN к АC?(также по свойству пропорции 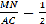 )Значит МN== 1/2AC .Мы доказали с вами что средняя линия равна половине основания треуголника.

Докажем что они параллельны.

Раз треугольники подобны значит углы все у них тоже равны,тоесть угол А=углуМ.

А какие это углы ?(соответсвенные) Следовательно…?(прямые MN и АCпараллельные по признаку параллельности прямых.)Что и требовалось доказать.

Запись в тетрадях доказательство теоремы.

Доказательство

МN-средняя линия трегольника АВС.Докажем ,что MN АC,и MN=AC.

1.Рассмотрим АВС и MBN: 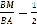 ; 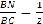(по определению средней линии),

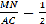; MN= AC(по свойству пропорции).

2.

3.1.Закрепление теоремы.

Давайте разберем задачу,которую мы не смогли решить .

Что такое MN?(средняя линия тр.)

Почему вы так решили?(Потому что соединяет середины сторон треуг.)

Что вы можете сказать о средней линии треуг.?(она параллельна основанию и равна ее половине).

Почеуму так?Как вы поняли это из доказательства?(так как треугольники подобны,значит углы соответсвенные равны,и следовательно по признаку параллельности прямых средняя линия и основание треугольника параллельны,а также маленький треугольник в 2 раза меньше большого,значит коэфицент подобия равен ½,следовательно средняя линия треуголника ,котороя является основанием маленького треугольника в 2 раза меньше основания большого трегольника,тоесть средняя линия треуг.равна половине основания данного треугольника).

Чему равна MN?(8см по свойству средней линии)

Работа по готовым чертежам. Научиться применять основное свойство ср. л. треугольника.

Задание: Найти неизвестный элемент, используя свойство ср. л.

треугольника.

3.2. Ребята, давайте решим такую задачу на применение данной теоремы: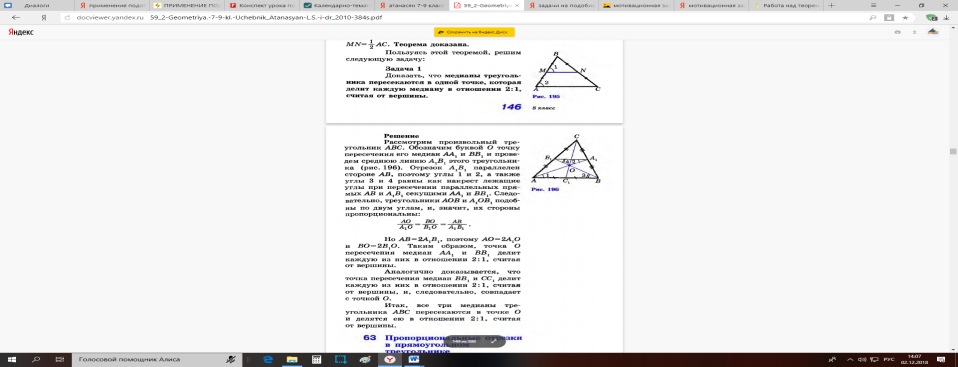
Решение.

1)-О чем идет речь в задаче? (о треугольнике и его медианах)

-Что нужно найти или доказать? (что медианы пересекаются в точке, которая делит каждую в отношении 2/1)

-заданы ли размеры треугольника? (нет, можем выбрать произвольно)

-Давайте начертим треугольник АВС, проведем его медианы и точку их пересечения назовем О.

2)Мы с вами не зря доказали теоремы о средней линии треугольника, давайте проведем ее в данном треугольнике АВС. Назовем ее В1А1.

Обозначим углы.

-Что вы можете сказать об отрезкеВ1А1 и АВ? (они параллельны)

_что тогда можно сказать об углах?( 1,2, 3,4 равны, как накрест лежащие при парал. Прямых и секущих)

-верно. А какими тогда будут треугольника АОВ и А1ОВ1?( подобные(по 2 признаку).

_А это значит, что какие-то стороны у них пропорциональны, какие? ( )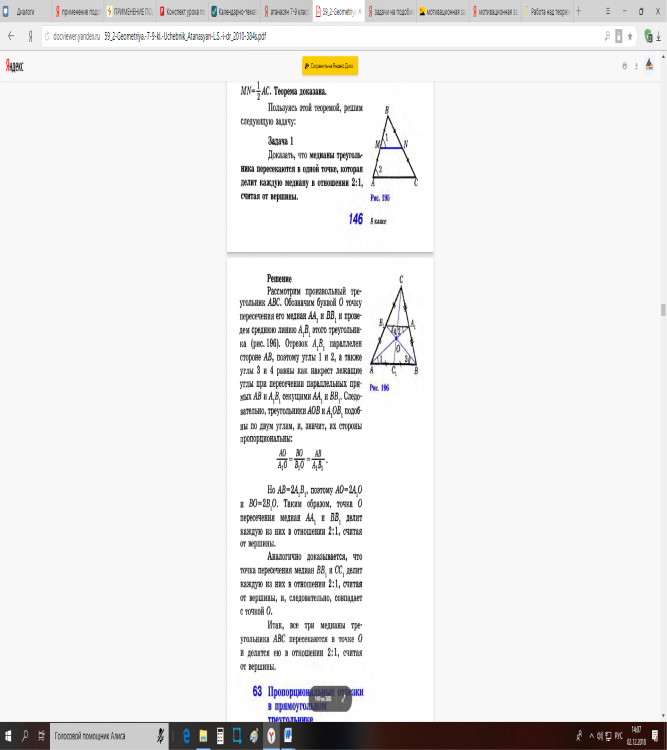

-Хорошо, а чему равны стороны АВ, ВО, АО? (АВ=2А1В1, ВО=2В1О, АО=2А1О)

-Какой вывод можно сделать? (что точка О делит медианы в отношении 2:1)

-Верно, вот мы с вами и решили задачу.

3.3.Применение теоремы

Работа в тетрадях

Задача 1 566

Точки P и Q-середины сторон АВ и АС треугольника АВС. Найдите периметр треугольника АВС ,если периметр треугольника APQ равен 21 см

Дано: АВС; PиQ-середины сторон АВ и АС

Р(APQ)=21см

Найти: Р(AВС)=? См

Решение : Так как Pи Q середины сторон АВ и АС АВ=2АР,АС=2А, ВС=2РQ.

(т.к PQ-средняя линия треугольника АВС(по определению ср.л))

Р(АВС)= АВ+ВС+АС=2(АР+РQ+AQ)=2*21=42см

Ответ: Р(АВС)= 42см

Задача 2 564

Дан треугольник со сторонами 8,7 и 5 см.Найдите периметр треугольника,вершнами которого я вляются середины сторон данного треугольника.

Дано:АВ=8см,ВС=7см,АС=5см

M,N,K-середины сторон АВ,ВС,АС

Найти Р(MNK)-?см

Решение

Р( MNK)= MN+NK+КМ

Так как M,N,K-середины сторон АВ,ВС,АС(по условию) MN,NK,КМ-средние линии треуг. АВС(по определению ср.л) КМ=АВ=4см,

МN=ВС=3,5см, N К=АС=2,5см Р( MNK)=4см+3,5см+2,5см=10см

Ответ: Р( MNK) =10см

3.4. Подведение итогов.

-Вспомните, что такое средняя линия треугольника? Какими свойствами она обладает? Чем мы пользовались при доказательстве этой теоремы?

8. Рефлексия.

Нарисуйте на полях тетради: квадрат-все понял, треугольник-не все понятно, круг-ничего не понятно.

9. Домашнее задание.

п. 62

• Выучить определение средней линии;

• Знать ее свойства

• Выучить доказательство .

• №565, 586

9