Цели урока:
- выяснить уровень знаний, умений и навыков учащихся решения текстовых задач;
- повторить основные приемы решения текстовых задач;
- развивать интерес к предмету.
Ход урока:
Слайд №3.
Сегодня мы совершим путешествие на планету Задача, население которой составляют текстовые задачи. План нашего путешествия изображен на схеме. В путешествие отправляется весь класс (экипаж ракеты) и вместе с нами наш друг мышонок «Пик».
Слайд №4. Разберем маршрут нашего путешествия.
Слайд №5.
Мы побываем с вами на « Площади движения», где вспомним основные приемы решения задач на движение; посетим «Космодром»; погуляем в «Волшебном саду», в котором встретимся с цветами – ромашками и ответим на их вопросы. Затем наш путь будет лежать через «Озеро неизвестности» к «Дому невыученных уроков». В дороге нам помогут строки стихотворения:
Не беда, что идти далеко,
Не боимся, что путь будет труден.
Никогда не давались легко
Достижения людям.
Слайд №6.
Решение задач на движение.
При решении задач на движение принимают такие допущения:
- движение считается равномерным (если нет специальных оговорок);
- скорость считается величиной положительной;
- повороты движущихся тел и переходы на новый режим движения считаются происходящими мгновенно.
При решении задач, связанных с равномерным движением, пользуются формулами s=vt, t=s/v, v=s/t, где t- время, v – скорость, s-пройденное расстояние.
Слайд №7.
Задача №1. Пешеход, идущий из дома на железнодорожную станцию, пройдя за первый час 3 км, рассчитал, что он опоздает к отходу поезда на 40 мин, если будет идти с той же скоростью. Поэтому остальной путь он прошел со скоростью 4 км/ч и прибыл на станцию за 15 мин до отхода поезда. Чему равно расстояние от дома до станции и с какой постоянной на всем пути скоростью пешеход пришел бы на станцию точно к отходу поезда?
Слайд №8.
Решение: Составим таблицу:
|
Пешеход пришел бы на станцию |
Расстояние, км |
Скорость, км/ч |
Время.ч |
|
Точно |
Х |
V |
x/v |
|
С опозданием |
Х-3 |
3 |
(x-3)/3 |
|
С опережением |
Х-3 |
4 |
(x-3)/4 |
Слайд №9.
Уравнивая промежутки времени, записанные в первой и второй, в первой и третьей строках, получаем систему уравнений:
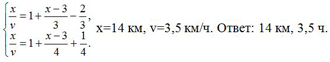
Замечание: средней скоростью движения на некотором участке пути называют постоянную скорость, с которой можно тот же участок пути пройти за то же время. Например, если турист шел 3ч со скоростью 5 км/ч и 2ч со скоростью 4 км/ч, то средняя скорость движения равна 4,6 км/ч.
Слайд №10.
Задача №2. Некоторое расстояние автомобиль преодолел в гору со скоростью 42 км/ч, а с горы со скоростью 56 км/ч. Какова средняя скорость движения автомобиля на всем участке пути?
Слайд №11.
Решение: Пусть длина участка пути равна s км. Тогда в оба конца автомобиль проехал 2s км, затратив на весь путь s/42+3/56=s/24ч. Средняя скорость движения равна 2s:(s/24)=48 км/ч. Ответ: 48 км/ч.
Слайд №12.
Задача №3. Два велосипедиста выезжают одновременно на встречу друг другу из пунктов А и В, расстояние между которыми 27 км. Через час велосипедисты встречаются и, не останавливаясь, продолжают ехать с той же скоростью. Первый прибывает в пункт В на 27 мин позже, чем второй в пункт А. Определите, скорость каждого велосипедиста.
Слайд №13-14.
Решение: пусть х км/ч – скорость велосипедиста из А, у км/ч - скорость велосипедиста из В, тогда (х+у) км/ч – скорость сближения; 27/(х+у)ч – время сближения. По условию 27/(х+у)=1.
27/х ч время в пути из А в В; 27/у ч – время в пути из В в А. по условию
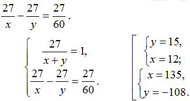
Ответ: 12км/ч – скорость велосипедиста из А, 15 км/ч – скорость велосипедиста из В.
Продолжим путешествие в ракете. Чтобы в нее попасть, надо преодолеть 9 ступенек, выполнив точные вычисления на каждой из них.
Слайд №15. устный счет
Слайд №16.Занявшим места в ракете определить параметры полета – скорость, время, расстояние.
Решить устно задачу:
Расстояние от Земли до планеты Задача равно 90 млн.км. Мы посылаем световой сигнал жителям планеты со скоростью 300000 км/ч. Через какое время на планете узнают, что к нам прибудут гости? Сколько времени мы будем находиться в полете, если скорость нашей ракеты 45 км/ч?
Решение:
1) 90000000 : 300000=300 (с)=5 мин.
2) 90000000 : 45= 2000000(с)
Слайд №17 В «Волшебном саду» произошло несчастье, начался пожар. Помоги потушить пожар решив задачу:
Две пожарные бригады, работая совместно при тушении лесного пожара, выполнят работу за 24 часа. Если сначала будет работать первая бригада и потушит половину всей площади возгорания, а затем её сменит вторая бригада и закончит тушение пожара, то на это потребуется 50 часов. За сколько часов каждая бригада в отдельности сможет потушить лесной пожар при условии, что огонь не будет распространяться?
Тема: Решение задач на движение по реке.
Слайд №18.
При решении задач на движение по реке принимают такие допущения:
- если тело, имеющее собственную скорость и, движется по реке, скорость течения которого равна v, то скорость тела по течению равна u+v, скорость против течения равна u-v.
- если из скорости по течению вы есть скорость против течения, то получится удвоенная скорость течения реки:
(u+v)-(u-v)=u+v-u+v=2v
Слайд №19. Задача № 5. Пароход от Киева до Херсона идет 3 суток, а от Херсона до Киева – 4 суток (без остановок). Сколько времени будут плыть плоты от Киева до Херсона?
Слайд №20.
Решение: Пусть x км – расстояние от Киева до Херсона, тогда скорость парохода по течению x/3 км/сут., против течения х/4 км/сут

Слайд №24.
« Дом невыученных уроков»
Жители « Дома невыученных уроков» решили отстроить себе дворец и стали закупать строительные материалы. Поскольку они считают не очень хорошо, то необходимо помочь им решить задачу:
« В двух ящиках было 135 кг гвоздей, причем в одном из них в 4 раза больше, чем в другом. Сколько килограммов гвоздей было в каждом ящике?»
Слайд №25.
Эту задачу решил мышонок «Пик». Проверьте его, пожалуйста, и если найдете ошибки то их исправьте:
|
1-й ящик |
2-й ящик |
Всего |
|
Х кг |
4х кг |
135 кг |
х + 4х =135, 5х=135, х = 135 : 5, х = 27
Ответ: в каждом ящике было по 27 гвоздей.
Слайд №26. конкурс «Ромашка»
В «Волшебном саду» каждому члену экипажа сорвать по лепестку с ромашками и ответить на содержащийся там вопрос
Вопросы к конкурсу составляются по теме которая вызывает наибольшее затруднение у учащихся.
Слайд №27.
Учитель задает индивидуальное домашнее задание учащимся:
Слайд №28. Пассажир знает, что на данном участке пути скорость этого поезда равна 40 км/ч. Как только мимо окна начал проходить встречный поезд, пассажир пустил секундомер и заметил, что встречный поезд проходил мимо окна в течение 3с. Определить скорость встречного поезда, если известно, что его длина 75 м.
Слайд №29.
Из пункта А в пункт В, расстояние между которыми 80 км, выехал автобус. В середине пути он был задержан на 10 мин., но, увеличив скорость на 20 км/ч, прибыл в пункт В во время. С какой скоростью автобус проехал первую половину пути?
Литература
1. Иванов М. А. Вступительные экзамены по математике в гимназии, лицеи и колледже с повышенными требованиями к подготовке поступающих. – М.:
КУДИЦ – ОБРАЗ, 1999.
2. Звавич Л. И. и др. Задания для подготовки к письменному экзамену по математике в 9 классе. – М.: Просвещение, 2000.
3. Шевкин А. В. Текстовые задачи. – М.: Просвещение, 1997.
4. Каганов Э. Д. 400 самых интересных задач с решениями по школьному курсу математики для 6-11 классов. М.- ЮНВЕС – 1997.
5. Под редакцией Сканави М. И. Сборник задач по математике с решениями. – М.: Издательский Дом ОНИКС: Альянс – В, 1999.
6. Фоминых Ю. Ф. Прикладные задачи по алгебре для 7-9 классов. – М.: Просвещение, 1999.

 Получите свидетельство
Получите свидетельство Вход
Вход


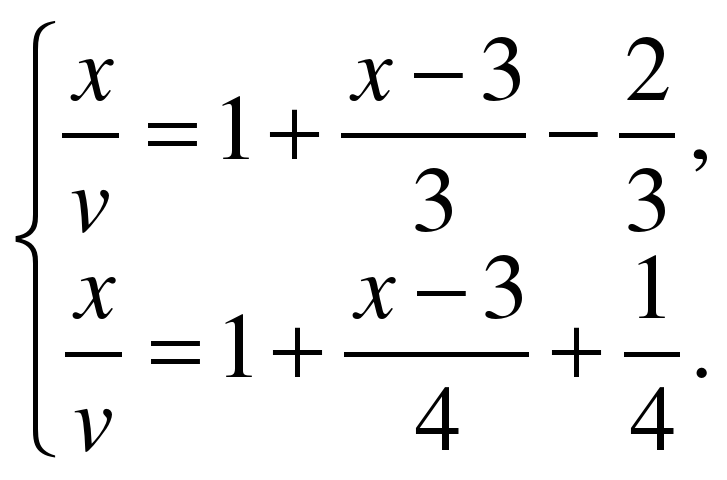 х=14 км, v=3,5 км/ч. Ответ: 14 км, 3,5 ч.
х=14 км, v=3,5 км/ч. Ответ: 14 км, 3,5 ч.
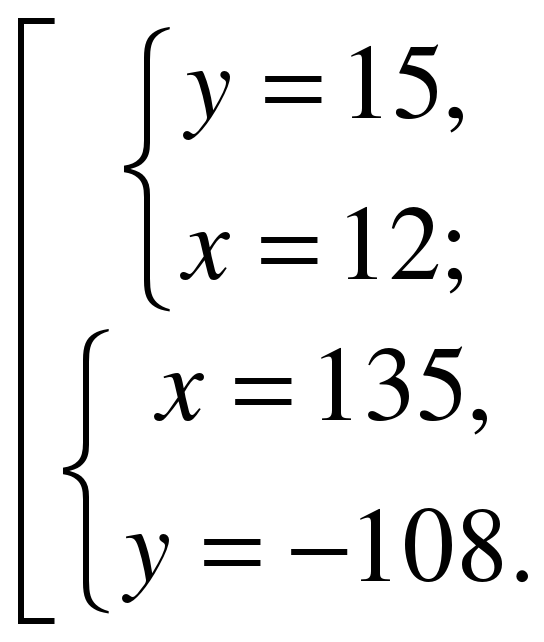 Ответ: 12км/ч – скорость велосипедиста из А, 15 км/ч – скорость велосипедиста из В.
Ответ: 12км/ч – скорость велосипедиста из А, 15 км/ч – скорость велосипедиста из В.








 Полёт на планету "Задача" (математика) (77 КB)
Полёт на планету "Задача" (математика) (77 КB)
 0
0 1113
1113 137
137 Нравится
0
Нравится
0



