Подготовка к ОГЭ по математике. 1 - 5 задание (план квартиры)

ОГЭ ПО МАТЕМАТИКЕ

ЗАДАНИЯ № 1-5

(план квартиры)

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ

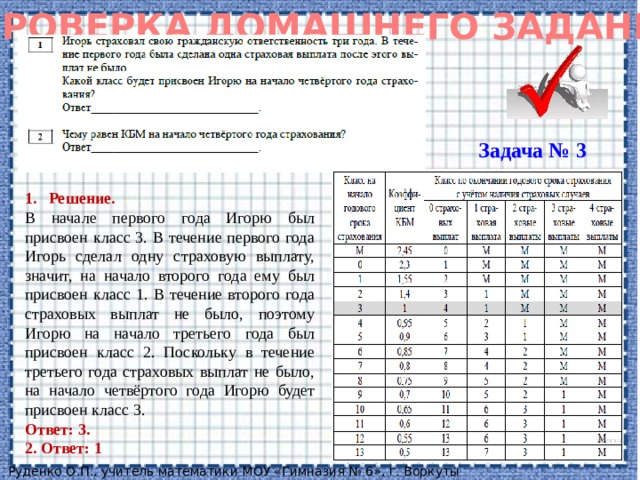
Задача № 3

• Решение.

В начале первого года Игорю был присвоен класс 3. В течение первого года Игорь сделал одну страховую выплату, значит, на начало второго года ему был присвоен класс 1. В течение второго года страховых выплат не было, поэтому Игорю на начало третьего года был присвоен класс 2. Поскольку в течение третьего года страховых выплат не было, на начало четвёртого года Игорю будет присвоен класс 3.

Ответ: 3.

2. Ответ: 1

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

Задача № 3

ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ

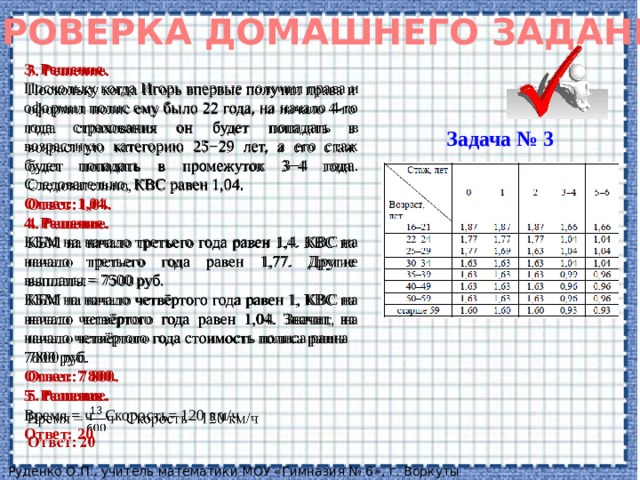
3. Решение.

Поскольку когда Игорь впервые получил права и оформил полис ему было 22 года, на начало 4-го года страхования он будет попадать в возрастную категорию 25−29 лет, а его стаж будет попадать в промежуток 3−4 года. Следовательно, КВС равен 1,04.

Ответ: 1,04.

4. Решение.

КБМ на начало третьего года равен 1,4. КВС на начало третьего года равен 1,77. Другие выплаты = 7500 руб.

КБМ на начало четвёртого года равен 1, КВС на начало четвёртого года равен 1,04. Значит, на начало четвёртого года стоимость полиса равна

7800 руб.

Ответ: 7 800.

5. Решение.

Время = ч Скорость= 120 км/ч

Ответ: 20

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ

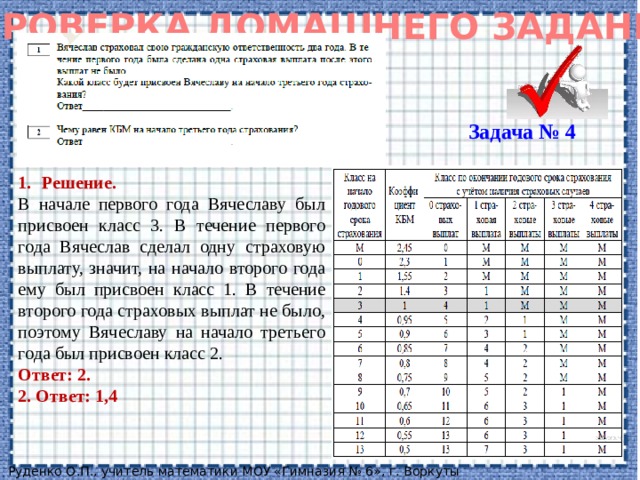
Задача № 4

• Решение.

В начале первого года Вячеславу был присвоен класс 3. В течение первого года Вячеслав сделал одну страховую выплату, значит, на начало второго года ему был присвоен класс 1. В течение второго года страховых выплат не было, поэтому Вячеславу на начало третьего года был присвоен класс 2.

Ответ: 2.

2. Ответ: 1,4

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

Задача № 4

ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ

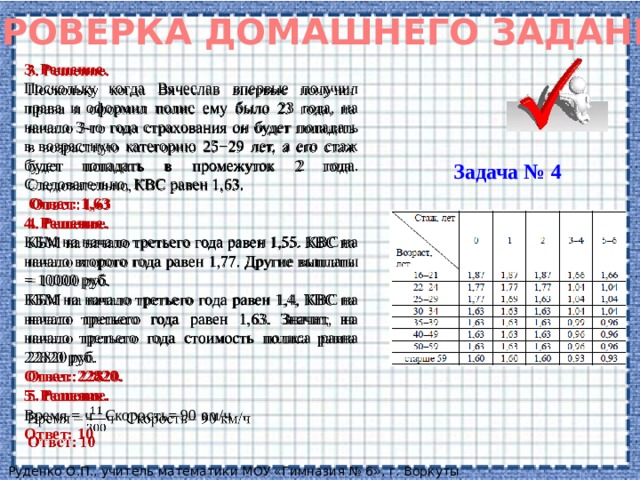
3. Решение.

Поскольку когда Вячеслав впервые получил права и оформил полис ему было 23 года, на начало 3-го года страхования он будет попадать в возрастную категорию 25−29 лет, а его стаж будет попадать в промежуток 2 года. Следовательно, КВС равен 1,63.

  Ответ: 1,63

4. Решение.

КБМ на начало третьего года равен 1,55. КВС на начало второго года равен 1,77. Другие выплаты = 10000 руб.

КБМ на начало третьего года равен 1,4, КВС на начало третьего года равен 1,63. Значит, на начало третьего года стоимость полиса равна 22820 руб.

Ответ: 22820.

5. Решение.

Время = ч Скорость= 90 км/ч

Ответ: 10

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

РАЗМИНКА

Ответ

0,2

1,35

18

0,5

0,25

6

0,6

2

Пример

Пример

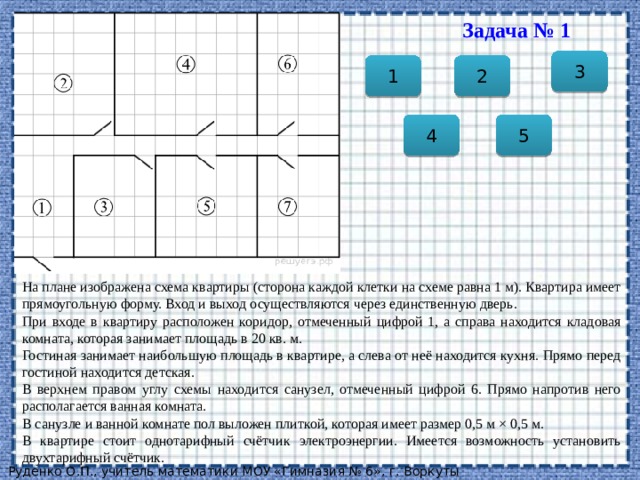
Задача № 1

3

1

2

4

5

На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Квартира имеет прямоугольную форму. Вход и выход осуществляются через единственную дверь.

При входе в квартиру расположен коридор, отмеченный цифрой 1, а справа находится кладовая комната, которая занимает площадь в 20 кв. м.

Гостиная занимает наибольшую площадь в квартире, а слева от неё находится кухня. Прямо перед гостиной находится детская.

В верхнем правом углу схемы находится санузел, отмеченный цифрой 6. Прямо напротив него располагается ванная комната.

В санузле и ванной комнате пол выложен плиткой, которая имеет размер 0,5 м × 0,5 м.

В квартире стоит однотарифный счётчик электроэнергии. Имеется возможность установить двухтарифный счётчик.

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

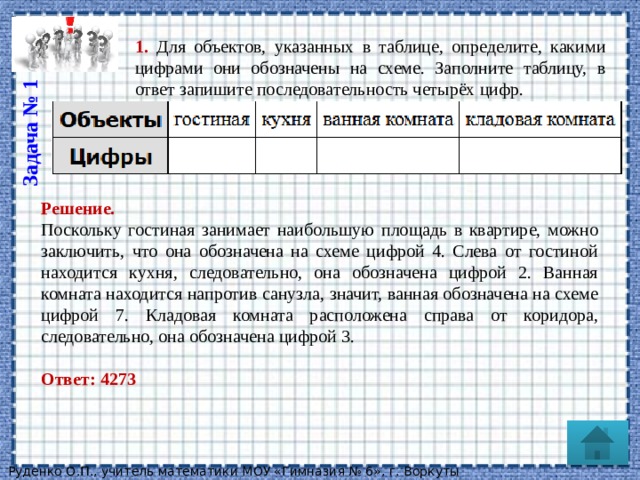
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Задача № 1

Решение.

Поскольку гостиная занимает наибольшую площадь в квартире, можно заключить, что она обозначена на схеме цифрой 4. Слева от гостиной находится кухня, следовательно, она обозначена цифрой 2. Ванная комната находится напротив санузла, значит, ванная обозначена на схеме цифрой 7. Кладовая комната расположена справа от коридора, следовательно, она обозначена цифрой 3.

Ответ: 4273

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

2. Плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол в ванной комнате и санузле?

Задача № 1

Решение.

Заметим, что, поскольку одна плитка имеет площадь 0,25 м 2 , чтобы выложить 1 м 2 пола плиткой, понадобится 4 плитки. Площадь санузла равна 6 · 4 = 24 м 2 . Площадь ванной равна 4 · 5 = 20 м 2 . Теперь найдём, сколько упаковок плитки понадобилось: = 35,2

Следовательно, чтобы выложить пол в ванной комнате и санузле понадобится 36 упаковок плитки.

Ответ: 36

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

3. Найдите площадь, которую занимает гостиная. Ответ дайте в квадратных метрах.

Задача № 1

Решение.

Сторона одной клетки равна 1 м. Значит, площадь гостиной равна:

7∙6=42 м 2 .

Ответ: 42.

4. Найдите расстояние от верхнего левого угла квартиры до нижнего правого угла квартиры (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение.

Найдём расстояние между двумя ближайшими точками по прямой верхнего левого угла квартиры и нижнего правого угла квартиры по теореме Пифагора:

Ответ: 20

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

5. Хозяин квартиры планирует установить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о тарифах оплаты, и их стоимости даны в таблице.

Задача № 1

Решение.

Разница в стоимости установки двухтарифного и однотарифного счётчиков равна 10 000 − 5 100 = 4 900 руб. День использования электроэнергии с однотарифным счётчиком стоит 2 · 3,5 · 24 = 168 руб./(кВт · ч). День использования электроэнергии с двухтарифным счётчиком стоит 3,5 · 2 · 17 + 3,5 · 1 · 7 = 143,5 руб./(кВт · ч). Разница в стоимости составляет 168 − 143,5 = 24,5 руб./(кВт · ч). Значит, экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного и однотарифного счётчиков через дней.

Ответ: 200.

Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

Задача № 2

3

1

2

4

5

Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м 2 . В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м 2 пола. Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м 2 между буфетом и плитой.

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

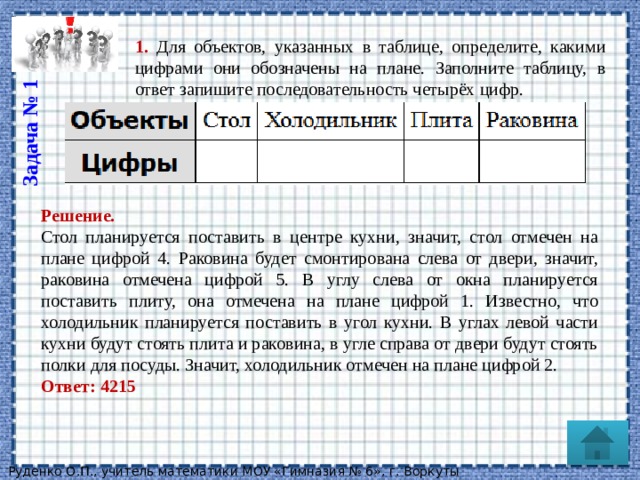
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Задача № 1

Решение.

Стол планируется поставить в центре кухни, значит, стол отмечен на плане цифрой 4. Раковина будет смонтирована слева от двери, значит, раковина отмечена цифрой 5. В углу слева от окна планируется поставить плиту, она отмечена на плане цифрой 1. Известно, что холодильник планируется поставить в угол кухни. В углах левой части кухни будут стоять плита и раковина, в угле справа от двери будут стоять полки для посуды. Значит, холодильник отмечен на плане цифрой 2. 

Ответ: 4215

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

2. Плитка для пола продаётся в упаковках по 5 штук. Сколько упаковок плитки нужно купить, чтобы покрыть пол кухни?

Задача № 2

Решение.

Заметим, что, поскольку одна плитка имеет площадь 0,09 м 2 , чтобы выложить пол в кухне понадобится столько плитки, сколько площади занимает кухня. Сторона одной клетки равна 0,3 м, значит, площадь кухни равна 9 · 0,3 · 9 · 0,3 = 7,29 м 2 . Теперь найдём, сколько плитки понадобится: Следовательно, чтобы выложить пол в кухне, понадобится упаковок плитки. Значит, необходимо купить 17 упаковок плитки.

Ответ: 17

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

3. Найдите площадь той части кухни, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м 2 .

Задача № 2

Решение.

Сторона одной клетки равна 0,3 м. Значит, площадь кухни равна:

0,3∙9∙0,3∙9= 7,29 м 2 .

Владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок между буфетом и плитой, который имеет площадь 0,18 м 2 . Холодильник занимает площадь 0,36 м 2 . На плане видно, что раковина и плита также занимают 0,36 м 2 . Буфет занимает 0,72 м 2 . Полки для посуды занимают участок площадью   0,3∙1∙0,3∙2=0,18 м 2 . Значит, площадь той части кухни, на которой будет смонтирован электрический подогрев пола, равна

7,29-0,18-0,18-0,72-0,36-0,36-0,36=5,13 м 2 .

Ответ: 5,13

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

4. Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах.

Задача № 2

Решение.

Найдём расстояние между противоположными углами обеденного стола по теореме Пифагора:

Ответ: 1,5

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

5. Владелец квартиры выбирает холодильник из двух моделей А и Б. Цена холодильников и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 4 рубля за кВт · ч.

Задача № 2

Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих холодильников? Ответ округлите до целого числа.

Решение.

Разница в стоимости холодильников равна 30000-28000= 2000 руб. Стоимость электроэнергии за сутки работы первого холодильника равна

4∙ 0,7=2,8 руб. Стоимость электроэнергии за сутки работы второго холодильника равна 4 ∙0,9=3,6 руб. Значит, при установке первого холодильника владелец квартиры за сутки экономит 3,6-2,8=0,8 руб. Следовательно, в год владелец квартиры экономит 0,8 ∙365=292 руб. Таким образом, экономия от меньшего расхода электроэнергии окупит разницу в цене этих холодильников через лет. Округлив, получаем ответ: через 7 лет.

Ответ: 7

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

Задача № 3

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.

При входе в квартиру расположен коридор, отмеченный цифрой 1. Перед входом в квартиру располагается санузел, а справа от него — ванная комната.

Гостиная занимает наибольшую площадь в квартире, а справа от неё находится кухня. Прямо перед гостиной находится детская. Из детской можно попасть на балкон, отмеченный цифрой 6.

Потолок в гостиной планируется покрасить в красный цвет. Для покраски одного 1 м 2 потолка требуется 0,25 л краски.

В квартире планируется установить счётчик электроэнергии. Имеется возможность установить однотарифный или двухтарифный счётчик.

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

Задача № 3

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

2. Краска продаётся в банках по 3 л. Сколько банок краски требуется купить, чтобы покрасить потолок в гостиной?

3. Найдите площадь, которую занимают детская и балкон. Ответ дайте в квадратных метрах.

4. Найдите расстояние между противоположными углами детской комнаты в метрах. Ответ запишите в виде

5. Хозяин квартиры планирует установить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о потребляемой мощности, и тарифах оплаты даны в таблице.

Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?

Руденко О.П., учитель математики МОУ «Гимназия № 6», г. Воркуты

Используемые ресурсы

https:// fipi.ru/oge

https://math-oge.sdamgia.ru /