Получите свидетельство
Вход
КЕГЭ 2021
Задание 14 (повышенный уровень)
Тема : Кодирование чисел. Системы счисления.
Чубарова Е.Г. МБОУ «СОЩ № 5 г. Гурьевска»
По материалам сайта http://kpolyakov.spb.ru
Демо версии 2019-2020
Что нужно знать :
• принципы кодирования чисел в позиционных системах счисления;
• правила перевода из 10-ной в любую другую с.с. и соотношение между 2-ной, 8-ной и 16-ной с.с. ;
• чтобы перевести число 12345 N , из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на в степени, равной ее разряду:
4 3 2 1 0 ← разряды
1 2 3 4 5 N = 1•N 4 + 2•N 3 + 3•N 2 + 4•N 1 + 5•N 0
• последняя цифра записи числа в системе счисления с основанием N – это остаток от деления этого числа на N
• две последние цифры – это остаток от деления на N 2 , и т.д.
• двоичная арифметика (сложение, вычитание, умножение)
Что нужно знать :
• число 2 N в двоичной системе записывается как единица и N нулей:
2 N = 10000….0 2
N
• число 2 N -1 в двоичной системе записывается как N единиц:
2 N - 1 = 11….1 2
N
• число 2 N –2 K при K
2 N - 2 K = 11….100…00 2
N-K K
• 2 N + 2 N = 2*2 N = 2 N+1
2 N = 2 N+1 - 2 N
- 2 N = - 2 N+1 + 2 N
Легче объяснить :
• число 10 N в десятичной (более привычной!) системе записывается как единица и N нулей:
10 N =10000….0 10 Пример: 10 4 =10000
N
• число 10 N -1 в десятичной системе записывается как N девяток (!):
10 N -1=99….9 10 Пример: 10 4 -1= 9999
N
• число 10 N –10 K при K
10 N -10 K =99….900…00 10 Пример: 10 5 -10 2 = 100000
N-K K 100
99900
5-2=3
2
переход к другим с.с. :
• число 3 N в троичной системе записывается как единица и N нулей:
3 N = 10000….0 3
N
• число 3 N -1 в троичной системе записывается как N двоек:
3 N – 1 = 222...2 3
N
• число 3 N –3 K при K
3 N - 3 K = 222…200…00 3
N-K K
Общая схема :
• число a N в с.с. c основанием a записывается как единица и N нулей:
a N = 10000….0 a
N
• число a N -1 в с.с. c основанием a записывается как N раз (a-1):
a N - 1 = (a-1)(a-1)…(a-1) a
N
• число a N –a K при K
a N – a K = (a-1)(a-1)…(a-1)00…00 a
N-K K
Пример с решением:
Сколько значащих нулей содержится в двоичной записи числа, которое можно представить в виде
8 510 + 4 1500 -16 ?
Алгоритм:
- Все переводим в степени двойки;
- NB! Как представить 16? (2 4 = 16)
- Выстраиваем всю запись по возрастанию степени (!!!);
2 3000 + 2 1530 – 2 4 =
2 3000 = 100000…000 (1 и 3000 нулей)
2 1500 - 2 4 = 11111…1111 0000 ( 1526 единиц и 4 нуля по формуле
a N – a K = (a-1)(a-1)…(a-1)00…00 a
N-K K)
Находим количество нулей: 3000 –1526 = 1474
Решаем с помощью программы. ч то нужно знать :
• функции div и mod (выполняются только для целых чисел и значение функций – целое число ( integer ))
- Возведение в степень a n – power (a, n). Значение функции вещественное число!
- Алгоритм перевода целого числа из 10 системы счисления в любую другую систему счисления с основанием q. (Алгоритм последовательного деления с выделением остатков)
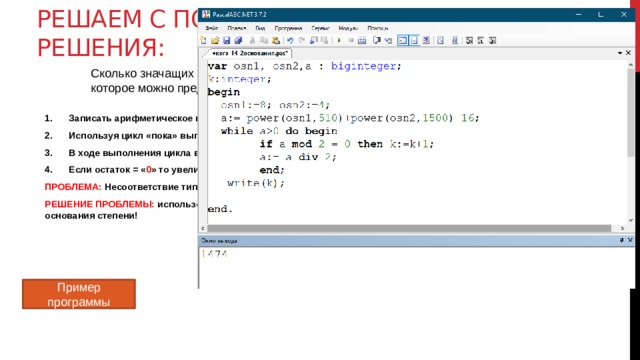
Решаем с помощью программы. Идея решения:
Сколько значащих нулей содержится в двоичной записи числа, которое можно представить в виде
8 510 + 4 1500 -16 ?
- Записать арифметическое выражение в программе.
- Используя цикл «пока» выполнить перевод в двоичную систему счисления.
- В ходе выполнения цикла выделять остатки и сравнивать их с « 0 ».
- Если остаток = « 0 » то увеличиваем счетчик на 1.
ПРОБЛЕМА: Несоответствие типов данных для функций power, mod и div!
РЕШЕНИЕ ПРОБЛЕМЫ: использование нового типа данных – biginteger для арифметического выражения и основания степени!
Пример программы
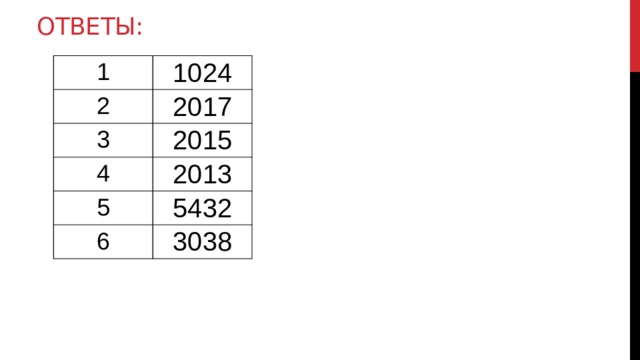
Примеры для самостоятельного решения
- Сколько единиц в двоичной записи числа 8 1023 + 2 1024 – 3?
3 = 4-1, 2 3069 + 2 1024 – 2 2 +2 0 !!! Избегать большого количества «-»
- Сколько единиц в двоичной записи числа 4 2016 + 2 2018 – 6?
6 = 8 – 2, 2 4032 + 2 2018 – 2 3 +2 1
- Сколько единиц в двоичной записи числа 4 2014 + 2 2015 – 9?
2 4028 + 2 2015 – 1001 2
- Сколько единиц в двоичной записи числа 4 2015 + 2 2015 – 15?
15 = 16 – 1, 2 4030 + 2 2015 – 2 4 + 2 0
- Сколько единиц в двоичной записи числа 8 2014 – 2 614 + 45?
45 = 101101 2 , 2 6042 – 2 614 + 101101 2
- Сколько единиц в двоичной записи числа 8 1014 – 2 530 – 12?
12 = 1100 2 , 2 3042 – 2 530 – 1100 2
Ответы:
1
1024
2
2017
3
2015
4
2013
5
5432
6
3038
Пример с решением:
Сколько единиц в двоичной записи числа 2 2014 – 4 650 – 38?
1294 единиц,
713 единиц,
6 нулей
1301 нуль
2 единицы,
3 нуля
1 единица,
1 нуль
Итого: 713 + 1294 + 2 + 1 = 2010
Использование - 2 N = - 2 N+1 + 2 N
Пример с решением:
Значение арифметического выражения: 9 8 + 3 5 – 2 – записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
4 двойки,
1 нуль
1 единица
1 единица,
16 нулей
2 = 3 - 1
Итого: 4
Пример с решением:
Значение арифметического выражения: 5∙36 7 + 6 10 – 36 записали в системе счисления с основанием 6. Сколько цифр «5» содержится в этой записи?
1 пятерка,
14 нулей
8 пятерок,
2 нуля
Итого: 8 + 1 = 9
Пример с решением:
Какая первая цифра в шестнадцатеричной записи числа 2 379 +2 378 +2 377 ?
1 единица,
379 нулей
1 единица,
378 нулей
1 единица,
377 нулей
11100000……….0000 2 переводим в 16 с.с. с помощью тетрад: 377:4 = 94 и 1 «0» в остатке
3 единицы,
377 нулей
Итого: 1110 2 =E 16
Пример с решением:
Сколько единиц в двоичной записи числа (2 4400 – 1)·(4 2200 + 2)?
1 единица,
8800 нулей
1 единица,
1 единица,
4400 нулей
1 нуль
2 4400 – 2 1 =1111111….11110
4399
Итого: 1 +4399 = 4400
Пример с решением:
Сколько единиц в двоичной записи числа (2 4400 – 1)·(4 2200 + 2)?
4400 единиц
1111
1010
1111
1111
1001011
Количество единиц не меняется!
Итого: 4400
Пример с решением:
Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8, 4. Часть символов при записи утеряна. Позиции утерянных символов обозначены знаком *:
X= *7* 16 = 5*6 8 = ***1* 4
Определите число X .
Представим все числа в 2 с.с.
*7* 16 = * * * * 0111 * * * * 2
5*6 8 = 101 * * * 1 1 0 2
***1* 4 = * * * * * * 0 1 * * 2
101110110 2
Итого: 101110110 2 = 374
Пример с решением:
Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8. Часть символов при записи утеряна. Позиции утерянных символов обозначены *:
X = *5 16 = *0* 8 .
Сколько чисел соответствуют условию задачи?
Представим все числа в 2 с.с.
*5 16 = * * * *01 01 2
*0* 8 = * * * 000 * * * 2
* * 000101 2
00
01
10
11
Итого: 3
Подготовка к КЕГЭ. Тема "Системы счисления". Разбор задания № 14 с программированием. (230.18 KB)
0
1414
20
Нравится
0
