 № 10 -№ 9 Анализирование информации, представленной в виде схем " width="640"
№ 10 -№ 9 Анализирование информации, представленной в виде схем " width="640"
Трансформация ОГЭ: задача № 11- № 10 -№ 9
Анализирование информации, представленной в виде схем
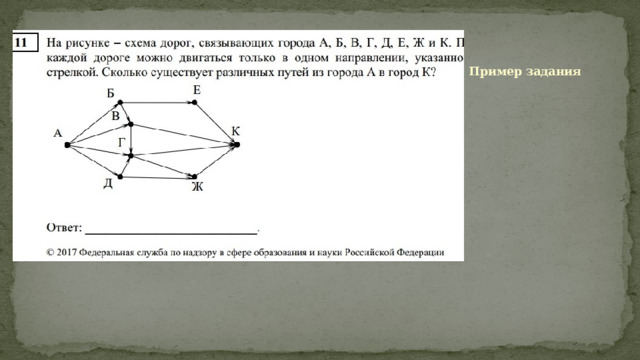
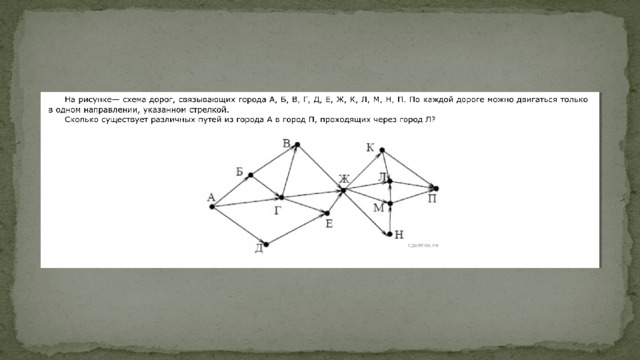
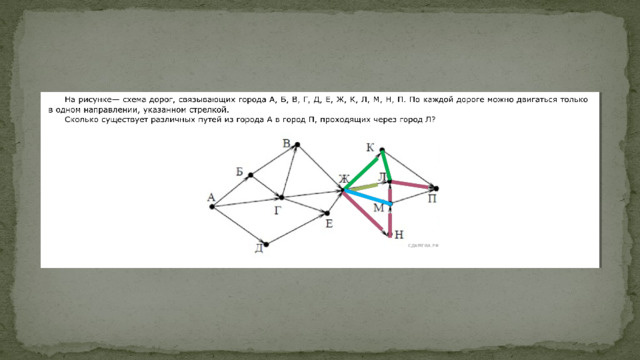
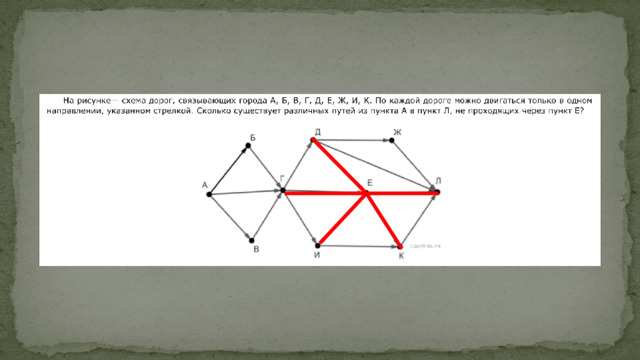
Пример задания

Общие подходы к решению задачи
Топология - сеть
Способы решения
1. Перебор
2. Дерево
3. Подсчёт
4. Уравнения
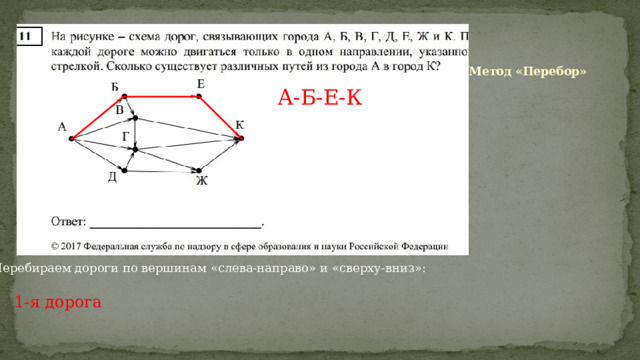
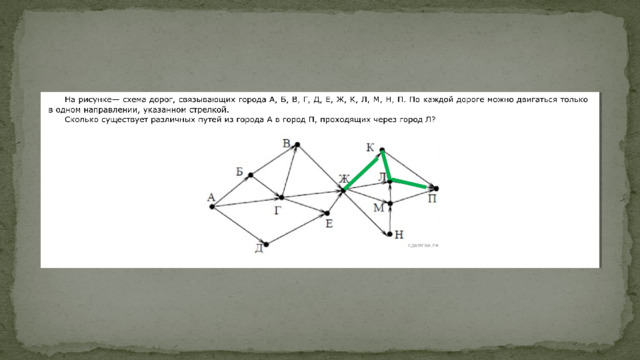
Метод «Перебор»
А-Б-Е-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
1-я дорога
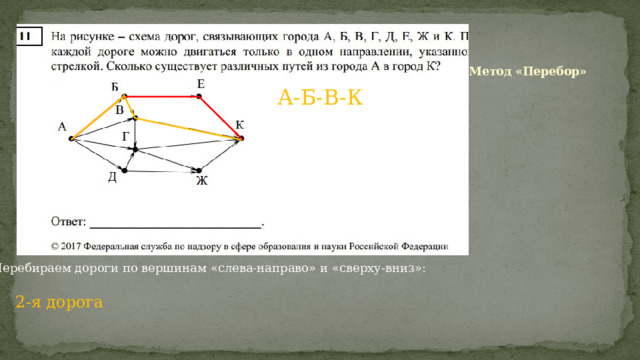
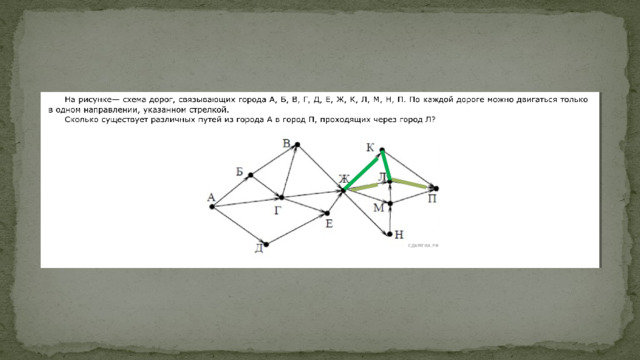
Метод «Перебор»
А-Б-В-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
2-я дорога
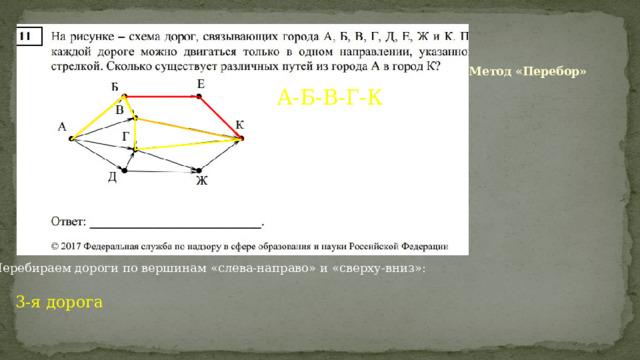
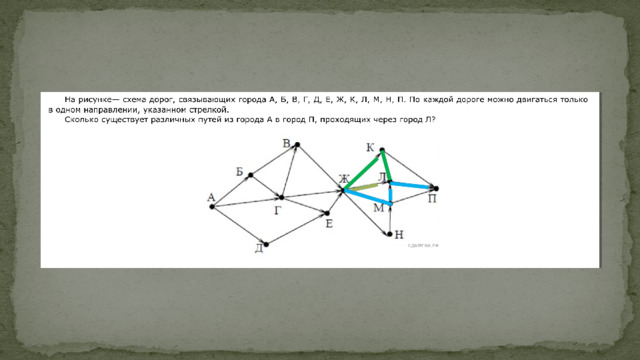
Метод «Перебор»
А-Б-В-Г-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
3-я дорога
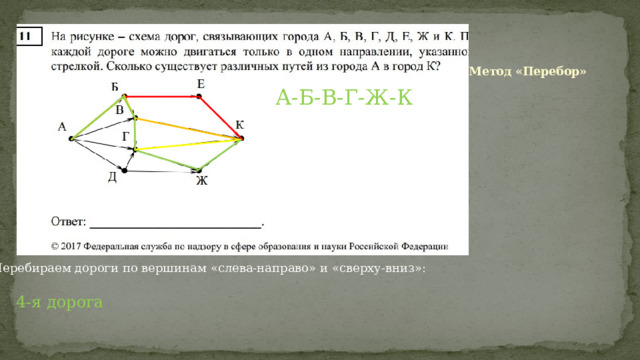
Метод «Перебор»
А-Б-В-Г-Ж-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
4-я дорога
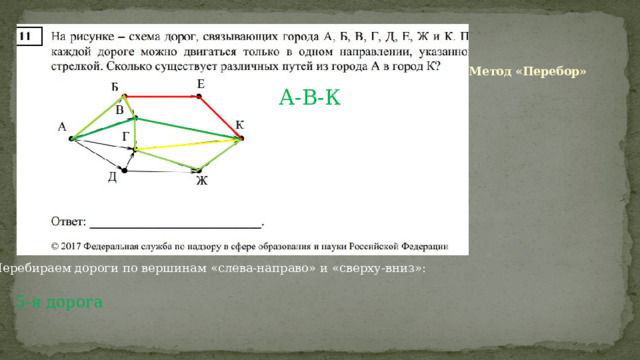
Метод «Перебор»
А-В-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
5-я дорога
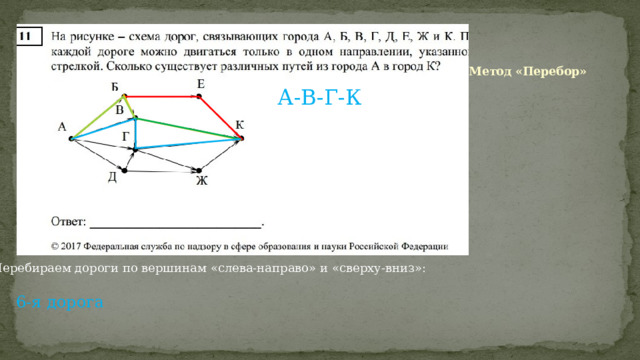
Метод «Перебор»
А-В-Г-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
6-я дорога

Метод «Перебор»
А-В-Г-Ж-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
7-я дорога

Метод «Перебор»
А-Г-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
8-я дорога

Метод «Перебор»
А-Г-Ж-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
9-я дорога

Метод «Перебор»
А-Д-Г-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
10-я дорога

Метод «Перебор»
А-Д-Г-Ж-К
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
11-я дорога

Метод «Перебор»
А-Д-Ж-К
12 дорог
Перебираем дороги по вершинам «слева-направо» и «сверху-вниз»:
12-я дорога
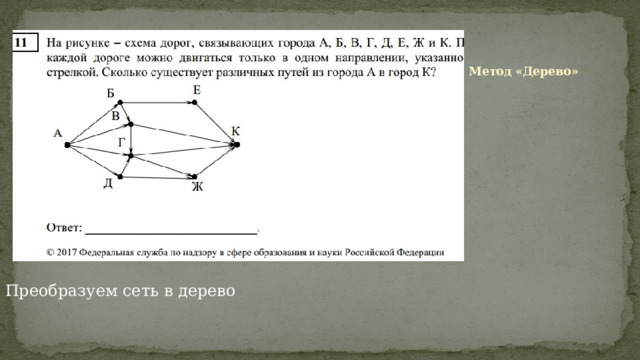
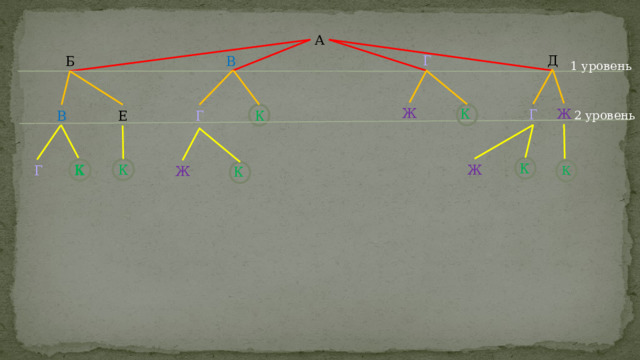
Метод «Дерево»
Преобразуем сеть в дерево

А
Д
Г
Б
В
1 уровень
А
Д
Г
Б
В
1 уровень
Ж
К
Ж
Г
Е
В
Г
К
2 уровень
К
Ж
К
К
Г
К
Ж
К
К
А
Д
Г
Б
В
1 уровень
1
Ж
К
Ж
Г
2
К
Г
Е
В
2 уровень
8
7
К
Ж
К
К
Г
К
Ж
5
К
4
К
3
К
6
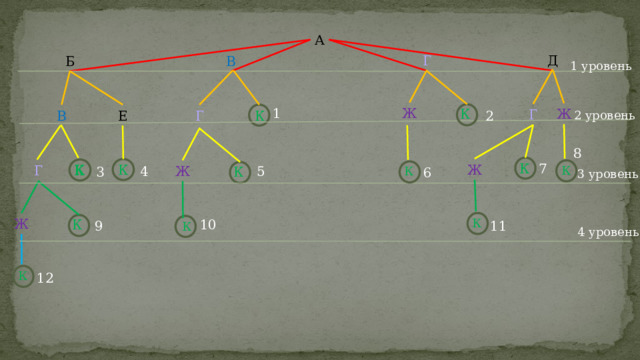
3 уровень
К
Ж
К
10
11
9
К
4 уровень
К
12
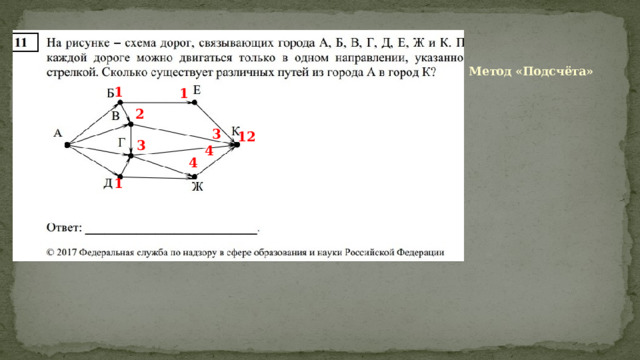
Метод «Подсчёта»
1
1
1
2
3
12
3
4
4
1
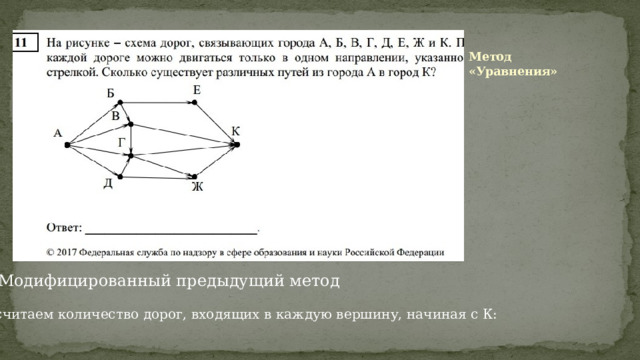
Метод «Уравнения»
Модифицированный предыдущий метод
Посчитаем количество дорог, входящих в каждую вершину, начиная с К:

1. Nк = Nе + Nв + Nг + Nж
2. Nе = Nб
Nx – сумма дорог, ведущих в город N
3. Nв = Nб + Nа
Количество уравнений = количеству городов
4. Nг = Nв + Nд + Nа
5. Nж = Nг + Nд
6. Nб = Nа
7. Nд = Nа
8. Nа = 1

1
1. Nк = Nе + Nв + Nг + Nж
1
1
2. Nе = Nб
Подставим во все уравнения, содержащие
вершину Nа , её значение, равное единице.
1
1
3. Nв = Nб + Nа
1
1
4. Nг = Nв + Nд + Nа
1
5. Nж = Nг + Nд
Таким образом нашли суммы дорог, ведущих
в города Б /Nб/ (2, 3, 6) ; Д /Nд/ (4,5,7) ;
Е /Nе/ (1, 2)
1
1
6. Nб = Nа
1
1
7. Nд = Nа
8. Nа = 1

4
1
2
1. Nк = Nе + Nв + Nг + Nж
1
1
2. Nе = Nб
Найдём сумму дорог в город В /Nв/ , второе
слагаемое в уравнении (1) из уравнения (3):
Nв = 2 (1, 3, 4)
1
1
2
3. Nв = Nб + Nа
1
4
1
2
4. Nг = Nв + Nд + Nа
4
1
5. Nж = Nг + Nд
Таким образом нашли суммы дорог, ведущих
в город Г /Nг/ (1, 4, 5) – третье слагаемое в
уравнении (1)
1
1
6. Nб = Nа
1
1
7. Nд = Nа
8. Nа = 1

5
4
2
1
1. Nк = Nе + Nв + Nг + Nж
1
1
2. Nе = Nб
Осталось найти сумму дорог в город Ж /Nж/,
Четвёртое слагаемое в уравнении (1) из
уравнения (5): Nж = 5 (1, 5)
1
1
2
3. Nв = Nб + Nа
1
4
1
2
4. Nг = Nв + Nд + Nа
4
5
1
5. Nж = Nг + Nд
Подставляя найденные величины в уравнение
(1) Найдём общее количество дорог, ведущих
в город К – 1 + 2 + 4 + 5 = 12
1
1
6. Nб = Nа
1
1
7. Nд = Nа
8. Nа = 1
Ответ: 12 дорог ведут из А в К

 Получите свидетельство
Получите свидетельство Вход
Вход











 Подготовка к ГИА по информатике (ОГЭ, 9 класс) (749.99 KB)
Подготовка к ГИА по информатике (ОГЭ, 9 класс) (749.99 KB)
 0
0 322
322 1
1 Нравится
0
Нравится
0



