Планирование курса по математике "Подготовка к ГИА"

Пояснительная записка

 Курс «Подготовка к ГИА по математике» направлен на восполнение недостающих знаний, отработку приемов решения заданий различных типов и уровней сложности вне зависимости от формулировки, а также отработку типовых заданий ГИА по математике на тестовом материале. Курс составлен на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки выпускников основной школы.

Программа предусматривает продолжительность образовательного процесса 34 учебных недели в течение учебного года, 2 занятия в неделю.

Цель данного курса: подготовка учащихся к сдаче ГИА, продолжению образования, повышение уровня их математической культуры.

Задачи:

 - сформировать у учащихся умение определять вид задания, твёрдо знать алгоритм решения;

 - сформировать высокий уровень активности;

 - развить интерес к математике;

 - способствовать профориентации.

 Данный курс имеет общеобразовательный, межпредметный характер, освещает роль и место математики в современном мире. Всего на проведение занятий отводится 68 ч. Изучение методов решения типовых задач можно провести в форме обзорных лекций с разбором ключевых задач. Курс состоит из трех модулей: Алгебра, Геометрия, Реальная математика. Изучаемый материал примыкает к основному курсу, дополняя его историческими сведениями, сведениями, важными в общеобразовательном или прикладном отношении, материалами занимательного характера при минимальном расширении теоретического материала. Данный курс поможет научить школьника технике работы с текстовыми заданиями и сдачи итоговой аттестации, которая содержит следующие моменты:

 - обучение постоянному самоконтролю времени;

 - обучении оценки трудности заданий и разумный выбор последовательности выполнения заданий –обучение спиральному движению по тексту, что предполагает движения от простых типовых к сложным;

 - обучение приемам мысленного поиска способа решений заданий.

 В ходе изучения материала данного курса целесообразно сочетать такие формы организации учебной работы, как практикумы по решению задач, лекции, беседа, тестирование, частично - поисковая деятельность. Развитию математического интереса способствуют математические игры (дидактическая, ролевая), викторины, головоломки. Необходимо использовать элементы исследовательской деятельности. После рассмотрения полного курса учащиеся должны иметь следующие результаты обучения:

 - уметь определять тип задания, знать алгоритм решения;

 - уметь применять полученные математические знания в решении жизненных задач;

 - уметь использовать дополнительную математическую литературу с целью углубления материала основного курса, расширения кругозора и формирования мировоззрения, раскрытия прикладных аспектов математики.

 В результате освоения содержания программы учащийся получает возможность совершенствовать и расширить круг умений, навыков и способов деятельности:

1) Познавательная деятельность.

Умение самостоятельно и мотивированно организовать свою познавательную деятельность. Создание идеальных и реальных моделей объектов, процессов.

2) Информационно - коммуникативная деятельность.

Поиск и извлечение нужной информации по заданной теме в источниках различного типа. Умение развернуто обосновать суждение, давать определения, приводить доказательства.

3) Рефлексивная деятельность.

Владение навыками организации: постановка общей цели и определение средств её достижения, конструктивное восприятие иных мнений и идей, учет индивидуальности партнеров по деятельности, объективное определение своего вклада в общий результат.

Формирование ключевых компетентностей:

 - готовность к самообразованию;

 - готовность к использованию информационных ресурсов;

 - готовность к социальному взаимодействию;

 - коммуникативная компетентность.

 Инструментарием для оценивания результатов могут быть: тестирование, творческие работы.

 Задачи курса:

 - изучить оригинальные приемы тестовых заданий;       

 - формировать твердое убеждение в успешности сдачи экзамена;

 - развивать исследовательские компетенции в решении математических задач;

 - повысить интерес к предмету.

В результате работы по программе учащиеся должны знать:

 - методы проверки правильности решения заданий;

 - методы решения различных видов уравнений и неравенств;

основные приемы текстовых задач, а также проверки правильности их решения;

методы решения геометрических задач.

методы нахождения статистических характеристик.

Календарно-тематическое планирование:

Весь материал – смотрите документ.

РАБОЧАЯ ПРОГРАММА

по курсу

ПОДГОТОВКА К ГИА ПО МАТЕМАТИКЕ

2 часа в неделю

всего 68 часов

Составитель Панфилова Надежда Ивановна

2014 г

Пояснительная записка

Курс «Подготовка к ГИА по математике» направлен на восполнение недостающих знаний, отработку приемов решения заданий различных типов и уровней сложности вне зависимости от формулировки, а также отработку типовых заданий ГИА по математике на тестовом материале. Курс составлен на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки выпускников основной школы.
Программа предусматривает продолжительность образовательного процесса 34 учебных недели в течение учебного года, 2 занятия в неделю.

Цель данного курса: подготовка учащихся к сдаче ГИА, продолжению образования, повышение уровня их математической культуры.

Задачи:

- сформировать у учащихся умение определять вид задания, твёрдо знать алгоритм решения;

- сформировать высокий уровень активности;

- развить интерес к математике;

- способствовать профориентации.

Данный курс имеет общеобразовательный, межпредметный характер, освещает роль и место математики в современном мире. Всего на проведение занятий отводится 68 ч. Изучение методов решения типовых задач можно провести в форме обзорных лекций с разбором ключевых задач. Курс состоит из трех модулей: Алгебра, Геометрия, Реальная математика. Изучаемый материал примыкает к основному курсу, дополняя его историческими сведениями, сведениями, важными в общеобразовательном или прикладном отношении, материалами занимательного характера при минимальном расширении теоретического материала. Данный курс поможет научить школьника технике работы с текстовыми заданиями и сдачи итоговой аттестации, которая содержит следующие моменты:

- обучение постоянному самоконтролю времени;

- обучении оценки трудности заданий и разумный выбор последовательности выполнения заданий –обучение спиральному движению по тексту, что предполагает движения от простых типовых к сложным;

- обучение приемам мысленного поиска способа решений заданий.

В ходе изучения материала данного курса целесообразно сочетать такие формы организации учебной работы, как практикумы по решению задач, лекции, беседа, тестирование, частично-поисковая деятельность. Развитию математического интереса способствуют математические игры (дидактическая, ролевая), викторины, головоломки. Необходимо использовать элементы исследовательской деятельности. После рассмотрения полного курса учащиеся должны иметь следующие результаты обучения:

- уметь определять тип задания, знать алгоритм решения;

- уметь применять полученные математические знания в решении жизненных задач;

- уметь использовать дополнительную математическую литературу с целью углубления материала основного курса, расширения кругозора и формирования мировоззрения, раскрытия прикладных аспектов математики.

В результате освоения содержания программы учащийся получает возможность совершенствовать и расширить круг умений, навыков и способов деятельности:

1) Познавательная деятельность.

Умение самостоятельно и мотивированно организовать свою познавательную деятельность. Создание идеальных и реальных моделей объектов, процессов.

2) Информационно-коммуникативная деятельность.

Поиск и извлечение нужной информации по заданной теме в источниках различного типа. Умение развернуто обосновать суждение, давать определения, приводить доказательства.

3) Рефлексивная деятельность.

Владение навыками организации: постановка общей цели и определение средств её достижения, конструктивное восприятие иных мнений и идей, учет индивидуальности партнеров по деятельности, объективное определение своего вклада в общий результат.

Формирование ключевых компетентностей:

- готовность к самообразованию;

- готовность к использованию информационных ресурсов;

- готовность к социальному взаимодействию;

- коммуникативная компетентность.

Инструментарием для оценивания результатов могут быть: тестирование, творческие работы.

Задачи курса:

- изучить оригинальные приемы тестовых заданий;

- формировать твердое убеждение в успешности сдачи экзамена;

- развивать исследовательские компетенции в решении математических задач;

-повысить интерес к предмету.

В результате работы по программе учащиеся должны знать:

- методы проверки правильности решения заданий;

- методы решения различных видов уравнений и неравенств;

• основные приемы текстовых задач, а также проверки правильности их решения;

• методы решения геометрических задач.

• методы нахождения статистических характеристик.

Должны уметь:

- проводить преобразования в степенных и дробно-рациональных выражениях;

• применять свойства арифметических и геометрических прогрессий

• решать различные текстовые задачи;

• уметь распознавать геометрические фигуры, различать взаимное расположение, изображать геометрические фигуры, выполнять чертежи по условию задачи;

• находить вероятности случайных событий в простейших случаях;

• использовать приобретенные знания в различных жизненных ситуациях, практической деятельности.

Содержание учебных модулей

АЛГЕБРА

1. Числа и числовые выражения, проценты.

Натуральные числа. Арифметические действия с натуральными числами. Свойства арифметических действий. Делимость натуральных чисел. Делители и кратные числа. Признаки делимости на 2,3,5,9,10. Деление с остатком. Простые числа. Разложение натурального числа на простые множители.

Нахождение НОД и НОК. Обыкновенные дроби. Действия с обыкновенными дробями. Десятичные дроби, действия с десятичными дробями.

Применение свойств для упрощения выражений. Тождественно равные выражения. Проценты. Нахождение процента от числа и числа по его проценту.

2. Буквенные выражения.

Выражения с переменными. Тождественные преобразования выражений с переменными. Значение выражений при известных числовых данных переменных.

3. Преобразование выражений. Формулы сокращенного умножения. Рациональные дроби.

Одночлены и многочлены. Стандартный вид одночлена, многочлена. Коэффициент одночлена. Степень одночлена, многочлена. Действия с одночленами и многочленами. Формулы сокращенного умножения. Способы разложения многочлена на множители. Рациональные дроби и их свойства. Допустимые значения переменных. Тождество, тождественные преобразования рациональных дробей. Степень с целым показателем и их свойства. Корень n-ой степени, степень с рациональным показателем и их свойства.

4. Уравнения и неравенства.

Линейные уравнения с одной переменной. Корень уравнения. Равносильные уравнения. Системы линейных уравнений. Методы их решения. Квадратные уравнения. Теорема Виета. Неравенства с одной переменной. Система неравенств. Методы решения систем неравенств.

5. Прогрессии: арифметическая и геометрическая.

Числовые последовательности. Арифметическая прогрессия. Разность арифметической прогрессии. Формула n-го члена и суммы n-первых членов арифметической прогрессии. Геометрическая прогрессия, знаменатель геометрической прогрессии. Формула n-го члена и суммы n-первых членов геометрической прогрессии. Сумма бесконечной геометрической

прогрессии.

6. Функции и графики.

Понятие функции. Функция и аргумент. Область определения и область значений функции. График и нули функции. Функция возрастающая и убывающая на отрезке. Линейная функция и ее свойства. Обратно - пропорциональная функция ее свойства и график. Квадратичная функция ее свойства и график. Степенная функция. Свойства четной и нечетной степенной функций. Чтение графиков функций.

ГЕОМЕТРИЯ

1. Геометрические величины (Длины. Углы. Площадь).

Определения многоугольников (треугольники, четырехугольники — параллелограмм, прямоугольник, квадрат, ромб, трапеция),их свойства. Признаки равенства и подобия треугольников. Отыскание неизвестных элементов, содержащихся в многоугольниках. Формулы площадей треугольника и четырехугольников.

1. Тригонометрия.

Понятие синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Теоремы синусов и косинусов. Вычисление площадей.

1. Движения на плоскости: поворот, параллельный перенос, симметрия.

2. Векторы на плоскости.

Понятие вектора, их виды. Равенство векторов. Скалярное произведение векторов.

РЕАЛЬНАЯ МАТЕМАТИКА

1. Текстовые задачи.

Задачи на движение и способы их решения .Задачи на вычисление объема и способы их решения. Задачи на процентное содержание веществ в смесях, сплавах и растворах и способы их решения.

2. Элементы статистики и теории вероятностей.

Среднее арифметическое, размах, мода. Медиана как статистическая характеристика. Методы решения комбинаторных задач:перебор возможных ситуаций, дерево вариантов, правило умножения. Перестановки, размещение, сочетания. Вероятность случайного события. Сложение и умножение вероятностей.

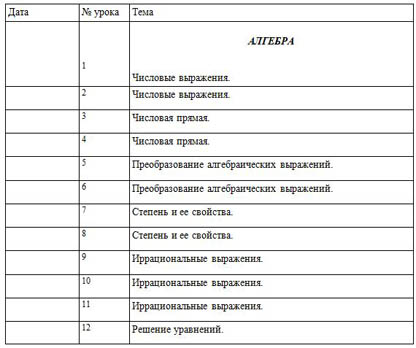
Календарно – тематический план

Литература

1.Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра.2014/ФИПИ.-М.:Интеллект-Центр.2010.-128с

2. Математика/Геометрия/ .Подготовка к ГИА.-Саратов:Лицей,2012.-64с

3. ГИА 2013.Математика:типовые экзаменационные материалы/под ред. А.Л. Семенова, И.В. Ященко. -М.: Издательство ,,Национальное образование,, , 2013. 192с.-/ГИА-2013.ФИПИ-школе/

4.Математика.9 класс. Тематические тесты для подготовки к ГИА 9.Алгебра,геометрия ,теория вероятностей и статистика: учебно-методическое пособие/под ред.Ф.Ф. Лысенко, С.Ю. Кулабухова. -Ростов н/Д: Легион-М,2011.-288с.-/ГИА-9/

Перечень сайтов

1.http://www.prosv.ru – сайт издательства ,,Просвещение,, /рубрика,,Математика,,/

2.http://www.drofa.ru-сайт издательства ,,Дрофа,, /рубрика,,Математика,,/

3.http://www.legion.ru-сайт издательства ,,Легион,,

4.http://www. fipi. ru-портал информационной поддержки мониторинга качества образования здесь содержится Федеральный банк тестовых заданий.

5.http://zadachi.mccme.ru-Задачи по геометрии :информационно-поисковая система.

6.http://www.intelekt centre.ru-Сайт издательства ,, Интеллект центр,,

Где можно найти учебно-тренировочные материалы, банк тренировочных заданий с ответами , методические рекомендации и образцы решений.

7.http://www.edu.ru-Центральный образовательный портал, содержит нормативные документы Министерства, стандарты и информацию о проведении эксперимента.