| Тип урока: изучение нового материала. Формы работы: коллективная, индивидуальная. Методы обучения: словесный, наглядный, практический. Оборудование: клей, ножницы, треугольник, развертка флексагона. Планируемые результаты обучения: Личностные : Ученик получит возможность научиться дисциплинированности, ответственному отношению к учебному труду, умению к совместной деятельности. Ученик получит возможность научиться самостоятельно добывать знания, любознательности. Метапредметные : Ученик получит возможность развивать пространственное воображение, геометрическое мышление Предметные : Ученик научится распознавать треугольник, его элементы, обозначение; Ученик научится конструировать флексагон.
Ход урока. 1.Оргмомент. Цель: включение в деловой ритм настрой на урок Положите свою ладошку на лист, лежащий перед вами. Обведите ладошку. Посмотрите на ладошку соседа. Ладошки получились разные. Почему они разные? Мы сами разные. Мыслим по-разному. Отвечаем по-разному. Но мы учимся понимать друг друга. Напишите на ладошке себе пожелание, как вы будете работать, отвечать, помогать другу, помогать соседу по парте. В конце урока проверим, смогли ли вы спрогнозировать свой успех. 2.Постановка познавательной задачи. Цель: организация учащихся по принятию познавательной задачи. Учитель: В Атлантическом океане есть место. Загадочное, интересное. О нем много написано, сняты фильмы. Это место, расположено между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида и называется “бермудским треугольником”. А ещё его называют “дьявольский треугольник”, “треугольник проклятых”. Загадочность его заключается в том, что в нём бесследно исчезают корабли и самолёты. Природа “бермудского треугольника” остаётся тайной и по сей день. -Во время моего небольшого рассказа прозвучало название фигуры, вам, наверное, известное. Так, какой геометрической фигуре посвятим наш урок? - Треугольнику. -Тема нашего урока “Треугольник”. (Запись на доске). Составим кластер по теме «Треугольник». (Работа групп по составлению вопросов для кластера). Что получилось? (Представлен кластер учеников) 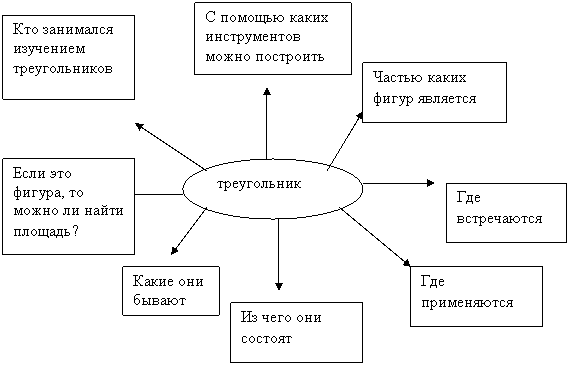 3.Усвоение новых знаний. Цель: ввести понятие треугольника, его элементов, обозначение; ознакомить учащихся со свойствами треугольника; побуждать детей “добывать” новые знания. - С какого вопроса начнем изучение темы? Рассматривается кластер ученика. Сравниваем с кластером учителя. Выясняем, что вопрос «что такое треугольник» в кластере не выделен. Заостряем вопрос на том, «какая фигура называется треугольником». В рабочих тетрадях отметим три точки, обозначим их прописными латинскими буквами А, В и С. Соедините их попарно ( по две) отрезками /на доске учитель изображает три точки , лежащие на одной прямой/. Что получили? У почему у меня не получился треугольник? - В одном случае Δ АВС, а в другом – треугольник не получился (треугольник “выродился” в отрезок). -Так что такое треугольник?/Учащиеся заполняют пропуски в определении треугольника на рабочих листах/. Сравниваются определения свои и на слайде. После показа вывод: -Треугольник – это геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, и трёх соединяющих их отрезков. - Вместо слова “треугольник” употребляют знак  . Запишем Δ АВС. Ребята, эти три точки, не лежащие на одной прямой, называются вершинами. Запишем. Отрезки – это стороны треугольника. Сколько их ? (Работа в парах) Записываем АВ, АС и ВС. Какие элементы есть еще у треугольника? (Выясняем, записываем). Итак, у треугольника есть три угла .Три стороны, три угла, три вершины – всё это элементы треугольника. А теперь рассмотрим свойства (слайд 5): - Учитель: У меня в руках четырёхугольник. Не меняя длины сторон, могу я изменить форму?/Да. Попробуйте/. А если взять треугольник? (Работа в группах. Ребята выясняют, можно ли изменить форму треугольника. Работа с моделями и со спичками) - Вывод (после обсуждения): Треугольник – “жесткая” фигура. Если заданы три его стороны, то форму треугольника уже изменить нельзя, не разрушив его. Это свойство широко используется на практике. Приведите примеры. Примеры: 1)Делая садовую калитку, обязательно прибивают планку /доску/, иногда две планки, чтобы получить треугольники. Это придаёт калитке прочность, иначе её перекосит. 2)Стропила зданий имеют вид треугольников. Это придаёт крепость и устойчивость. 3)При строительстве любых мостов в их конструкциях также присутствуют треугольники. 4)Ножки стула крепятся планками, чтобы стул был устойчивым. Чем больше треугольников в любой конструкции, тем она прочнее. Учитель: Как вы думаете, чему равна сумма углов любого треугольника? (Заслушать ответы). Давайте это выясним, верны ли ваши предположения. Предлагаю провести измерения углов с помощью транспортира. Какие результаты получились? Заслушать. Выясняем, что сумма углов у всех получилась разная. (Выясняем, что так может получиться потому, что приложили транспортир неточно, небрежно выполнили подсчет и т.д.) Я предлагаю найти сумму углов треугольника другим способом. Возьмите картонные треугольники, которые лежит у вас на столе. У всех они разные. Обведем в рабочих листах треугольник. Обозначим углы этого треугольника числами 1, 2 и 3. Отрежем ножницами все углы. Будем собирать их в одной общей точке. /Cтороны обводим, прикладываем линейку к сторонам крайних углов/. Замечаем, что все углы треугольника в сумме образуют развернутый угол, величина которого равна 180°. Так чему же равна сумма углов треугольника? - Сумма углов треугольника равна 180°. /Учащиеся записывают в рабочих листах/. Примем за основу этот факт. Но в 7 классе это утверждение рассмотрим подробнее. 4.Физкультминутка.(под музыку) Раз – согнуться, разогнуться,
Два – нагнуться, потянуться.
Три – в ладоши три хлопка,
Головою три кивка.
На четыре – руки шире,
Пять, шесть – тихо сесть.
Семь, восемь – лень отбросим. 5. Учитель: Продолжим знакомство с треугольниками А как вы думаете есть ли в пространстве у треугольника родственники ? (заслушать ответы детей) -У треугольника есть пространственные родственники (демонстрация моделей). Модели есть в группах. 1) тетраэдр, ( смотрим слайд 8) 2) октаэдр, 3) икосаэдр. А почему эти геометрические тела являются родственниками треугольника?(Ученики рассматривают модели, обсуждают вопрос. Делают вывод) -Ученики: Грани этих тел – треугольники. Давайте с вами сконструируем геометрическую бумажную игрушку, которая тоже является родственником треугольника, так как её поверхность состоит из треугольников. Эта игрушка называется флексагон . Она удивительна тем, что внезапно изменяет свою форму и цвет. Для получения этой игрушки возьмем развертку, лежащую у вас на столе. Она состоит из 10 треугольников трёх цветов (красный, зелёный и жёлтый). Собираем и склеиваем флексагон вместе. Одна сторона зелёная, другая жёлтая. Превратим его в красный флексагон. Игрушка вам понравилась? Пусть флексагон останется доброй памятью о нашем уроке, который был посвящен треугольнику. Флексагон складывают из полоски бумаги, предварительно размеченной на 10 равносторонних треугольников (раскрасить тремя цветами красок):
  
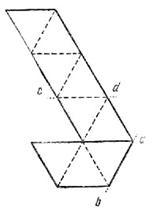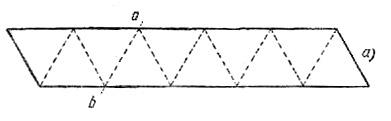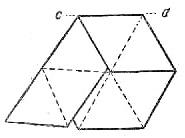
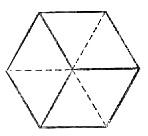
Полоску перегибают по линии ab и переворачивают: Перегнув полоску еще раз по линии cd, расположим ее концы так, чтобы предпоследний треугольник оказался наложенным на первый: Последний треугольник нужно подогнуть вниз и прикрепить к оборотной стороне первого треугольника: Развертку флексагона нужно перечертить и вырезать из полоски достаточно плотной бумаги шириной около 3-4 см. Чтобы "открыть" флексагон, его нужно одной рукой взять за два соседних треугольника примыкающих к какой-нибудь вершине шестиугольника (а), а другой рукой потянуть за свободный край двух противоположных треугольников (б). Если флексагон не открывается, нужно попробовать ухватить его за два других треугольника. При открывании шестиугольник выворачивается наизнанку, и наружу выходит поверхность, которая ранее скрывалась внутри. 6.Домашнее задание. /Дифференцировано/ -А теперь задание на дом.
Выполните рисунок с изображением применения “жесткости” треугольника в быту. По желанию сочинить небольшое стихотворение о треугольнике или флексагоне. Выбрать вопрос из кластера и подготовить к следующему уроку (слайд 9,10). 7.Итог. -Подведем итог урока, помощником возьмем стихотворение Льва Шеврина: Ты на него, ты на меня,
На всех нас посмотри.
У нас всего, у нас всего,
У нас всего по три.
Три стороны и три угла
И столько же вершин.
И трижды-трудные дела
Мы трижды совершим. -О какой геометрической фигуре идет речь в стихотворении? -О треугольнике. -“ Три стороны и три угла И столько же вершин”. Чему посвящены эти строки? -Элементам треугольника. -Какие “трудные дела мы трижды совершили”? -1)Определили, что такое треугольник. 2)Рассмотрели два свойства треугольника. 3)Говорили о пространственных родственниках треугольника. Сконструировали флексагон. 8.Резерв. (на столах в группах лежат рисунки треугольника Пенроуза) (слайд 11) - Плоский рисунок может обманывать, изображая невозможное. Я предлагаю рассмотреть невозможный пространственный объект - треугольник Пенроуза. Закройте одну из вершин этого треугольника, и станет ясно, что одна из его сторон направлена к нам, а другая – от нас, т. е. они не могут соединиться в пространстве.
Приложение | 
Получите свидетельство
Вход
ПЛАН-КОНСПЕКТ УРОКА Тема урока: Треугольник. (103 KB)
0
907
31
Нравится
0
