КГУ «Чермошнянская средняя школа»
Тайыншинского района
Северо-Казахстанской области,
учитель математики
Борович Ольга Вениаминовна
Урок алгебры и начал анализа по развитию математической грамотности в 11 классе «Общие методы решения уравнений. Решение нестандартных уравнений»
Цель: Знать общие методы решения уравнений, уметь применять их при решении стандартных и нестандартных уравнений; уметь решать уравнения используя свойства входящих в уравнение функций.
Задачи:
Образовательные: 1. Создание условий для открытия новых знаний: решение уравнений с использованием свойств, входящих в них функций;
2. Формирование умений и навыков правильно определять соответствующий метод, и применять его при решении уравнения любого вида.
Развивающие: 1. Развитие и совершенствование умений применять знания в нестандартных задачах;
2. Развитие ключевых компетенций учащихся;
3. Развитие математической культуры, умения анализировать, делать выводы;
4.Развитие познавательного интереса к изучаемому материалу, логического мышления.
Воспитательные: 1. Воспитание трудолюбия, терпения доводить начатое дело до конца;
2. Воспитание сознательности, ответственности за свое будущее;
3. Воспитание культуры общения, умение слушать других, проявлять взаимоуважение.
Ожидаемые результаты:
Учащиеся сопоставляют способы решения уравнений, анализируют, логически мыслят, обобщают и систематизируют.
Учащиеся вдумчиво читают текст, умеют выделить основные аспекты в изучаемой информации
Учащиеся умеют взаимодействовать в парах
Учащиеся демонстрируют продвижение от незнания к знанию
Учащиеся умеют защищать свой выбор, аргументировать свое мнение, демонстрируют владение математическим языком, знанием изучаемого учебного материала
Ход урока:
I этап-Стадия вызова: Проверка домашнего задания. Актуализация опорных знаний.
Учитель: Напомните , что вам было задано на дом.
Учащиеся: Решить уравнения, назвать способ, который применили.
Учитель: Какие способы решения уравнений вы выделили, есть ли повторяющиеся способы, для какого вида уравнений применяется данный способ. По ответам учащихся составляется схема. (слайды 1-5)
| Общие методы |


| Метод замены уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x) | Метод разложения на множители | Метод введения новой переменной | Функционально-графический метод |
В чем суть каждого метода? Для какого вида уравнений применяется данный способ? Приведите примеры, опираясь на таблицу.
Учитель: Обратите внимание на слайд, какие из рассмотренных способов можно было применить для решения следующих уравнений:
| уравнение | Способ решения |
| (x-3)4 +(x2-2x-3)10 =0 |
|
| log2 (5+3cos (3x- |
|
|
|
|
| 2x +3x =2*5x |
|
| sin25x+1=cos23x |
|
| sin(x3 +2x2 +1)=x2 +2x+3 |
|
Учащиеся убеждаются, что применяемые ранее способы для решения этих уравнений не подходят. В чем причина? То , что эти уравнения, надо решать другим способом, говорит уже тот факт, что в уравнении например 2,в левой и правой частях- функции, уравнения с которыми решаются принципиально разными способами, т.е логарифм и синус, или еще в 6 уравнении в правой части многочлен, в левой тригонометрическая функция.
Учитель: К какому выводу мы сейчас пришли?
Учащиеся: мы пришли к необходимости рассмотреть еще какие-то дополнительные способы, и исходя из уравнений в таблице, этих способов должно быть несколько.
II этап-стадия осмысления
Основная идея новых методов, которые в основном применяются для решения нестандартных уравнений, состоит в использовании свойств функций входящих в уравнение. Какие свойства, и как их использовать, вы узнаете, поработав в парах, где каждая пара рассмотрит примеры на применение одного свойства, затем вы познакомите присутствующих с рассмотренным методом. После выступления каждой группы, мы вместе определим способы и решим уравнения из таблицы.
Самостоятельная работа по заготовленным текстам. Работают 4 группы (10 минут).
Выступление каждой пары или одного из пары (2-3мин)
Решение уравнений из таблицы:
Решите уравнение (x-3)4 +(x2 -2x-3)10 =0
Используя свойства функций, можно заметить, что нет необходимости возводить двучлен в квадрат, и трехчлен в десятую степень, а заметим, что 4 и10 четные числа, следовательно (x-3)4 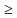 0 при любом значении x и (x2 -2x-3)
0 при любом значении x и (x2 -2x-3) 0 при любом значении x. Равенство в уравнении возможно, если только каждое слагаемое одновременно будет равно 0, (x-3)4 =0 и (x2 -2x-3)10 =0, корень первого уравнения x=3,корни второго уравнения
0 при любом значении x. Равенство в уравнении возможно, если только каждое слагаемое одновременно будет равно 0, (x-3)4 =0 и (x2 -2x-3)10 =0, корень первого уравнения x=3,корни второго уравнения
x=-1 и x=3. Число x=3 является корнем обоих уравнений, значит это и есть корень уравнения. Ответ: x=3
Решите уравнение:
![]()
Решение 1. Оценим, в каких пределах может принимать значения левая часть неравенства:
![]()
![]()
![]()
Так как все части неравенства положительны, прологарифмируем неравенство:
![]()
![]()
Итак, левая часть неравенства больше или равна единице.
2. Оценим, в каких пределах может принимать значения правая часть неравенства:
![]()
Получили, что правая часть неравенства меньше или равна единице.
Равенство возможно, только если обе части одновременно равны 1.
Найдем при каких значениях x выполняется равенство
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Итак, левая часть уравнения равна 1 при
Найдем при каких значениях х правая часть равна 1.
если
Итак, правая часть уравнения равна 1 при
Это решение должно совпадать с тем значением x при котором левая часть равна 1.
Выпишем значения из промежутка
:
При
При
При
При При
– эта точка совпадет с первой точкой и цикл начнется снова.
Вспомним, что левая часть уравнения равна 1 при Выпишем значения x из промежутка
При
При
При
При – эта точка совпадает с первой точкой, и цикл начинается снова.
Мы видим, что при обе части уравнения равны 1.
Итак, решение уравнения
Решите уравнение: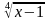 +2
+2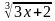 = 4+
= 4+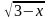
Данное уравнение невозможно решить общими методами, но используя ОДЗ данное уравнение решается просто: ОДЗ определяется системой неравенств или двойным неравенством
.
Значение корня кубического существует при любом х. Нетрудно проверить какие числа из ОДЗ являются корнями, проверкой находим что х=2 является корнем данного уравнения. Далее по свойству монотонности функций, на отрезке функция f(x)=
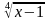 +2
+2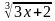 возрастающая, а функция g(x)=4+
возрастающая, а функция g(x)=4+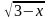 убывающая, поэтому , если уравнение f(x)= g(x) имеет корень на
убывающая, поэтому , если уравнение f(x)= g(x) имеет корень на , то этот корень единственный. Приходим к выводу, что х=2 –единственный корень уравнения.
Решите уравнение: 2x +3x =2*5x
Решение: разделим обе части уравнения на 5x
+
f(x)=
+
-убывающая функция, а следовательно, уравнение f(x)=2 не может иметь более одного корня.
Очевидно,что этим единственным корнем будет x=0;
Решите уравнение: sin25x+1=cos23x
Решение: данное уравнение решается с использованием ограниченности функций y=sin x и y=cos x
sin25x+1- cos23x=0
sin25x+ sin2 3x=0 исходное уравнение равносильно системе:
Приравнивая правые части двух последних равенств, получаем уравнение: =
, то есть 3n=5k n, k
. Это уравнение имеет решение
l
подставляя значения n или k в решение исходного уравнения, получаем:
=
, l
Ответ: х= , l
Решите уравнение: sin(x3 +2x2 +1)=x2 +2x+3
Решение: для любого действительного числа х имеем sin(x3 +2x2 +1) ,
x2 +2x+3=(х+1)2 +2 . Поскольку для любого значения х левая часть уравнения не превосходит единицы, а правая часть всегда не меньше двух, то данное уравнение не имеет решений.
Ответ: нет решений.
Вопрос: Какие свойства функций были использованы при решении этих нестандартных уравнений? Как вы считаете, можно ли приемы использования свойств функций применять при решении неравенств? Этим мы займемся на следующем уроке.
Задание на дом: № 344,№345, №346 стр 154
III стадия Рефлексия
«Оцени себя на уроке» учащимся предлагается анкета для оценки собственной деятельности на уроке, подведения итогов усвоения материала.

 Получите свидетельство
Получите свидетельство Вход
Вход



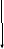 решения уравнений
решения уравнений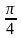 ))=sin2 (2x -
))=sin2 (2x - 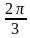 )
)








 План-конспект урока алгебры 11 класс по теме "Общие методы решения уравнений.Решение нестандартных уравнений" (57.82 KB)
План-конспект урока алгебры 11 класс по теме "Общие методы решения уравнений.Решение нестандартных уравнений" (57.82 KB)
 0
0 170
170 26
26 Нравится
0
Нравится
0


