МБОУ лицей «Вектор», г. Хабаровск Учитель математики Собко Людмила Александровна
Конспект урока «Первый признак равенства треугольников» ( 7класс, геометрия, учебник Атанасяна Л.С.)Цели урока:
Обучающая:
Доказательство первого признака равенства треугольников;
Формирование умения применять первый признак равенства треугольников при решении задач, находя в треугольниках три пары соответственно равных элементов.
Развивающая:
Выработка умения сопоставлять, обобщать полученные выводы, оценивать влияние условий на результат,
Развитие навыков правильной математической речи, логического мышления учащихся.
Воспитательная:
Выработка умения анализировать данные, выводить логические следствия из данных предпосылок, умение делать выводы.
Выработка умения концентрировать внимание, сосредотачиваться в процессе получения новых знаний.
Формирование положительного отношения к предмету, интерес к знаниям.
Методическая цель: опробовать новый подход к формулировке теоремы, выяснить уловят ли учащиеся момент, когда условия становятся достаточными.
Тип урока: комбинированный.
Оборудование: интерактивная доска, презентация, линейка, треугольник, цветные маркеры, набор треугольников для практической работы.
Ход урока
1. Организационный момент: (2 мин)
- Дорогие ребята, продолжаем наше путешествие по стране «Геометрия». На предыдущем уроке мы прибыли в город «Треугольники». Выяснили, что треугольник – загадочная фигура, таящая в себе тайны, как и Бермудский треугольник в далеком океане. Первое, что мы узнали, что треугольник, это геометрическая фигура … ( ответ ученика). Выяснили, что среди их множества есть равные треугольники. Сегодня продолжим разговор о равных треугольниках. И узнаем еще одну их тайну.
2. Актуализация знаний учащихся: (6 мин)
Повторим материал прошлого урока.
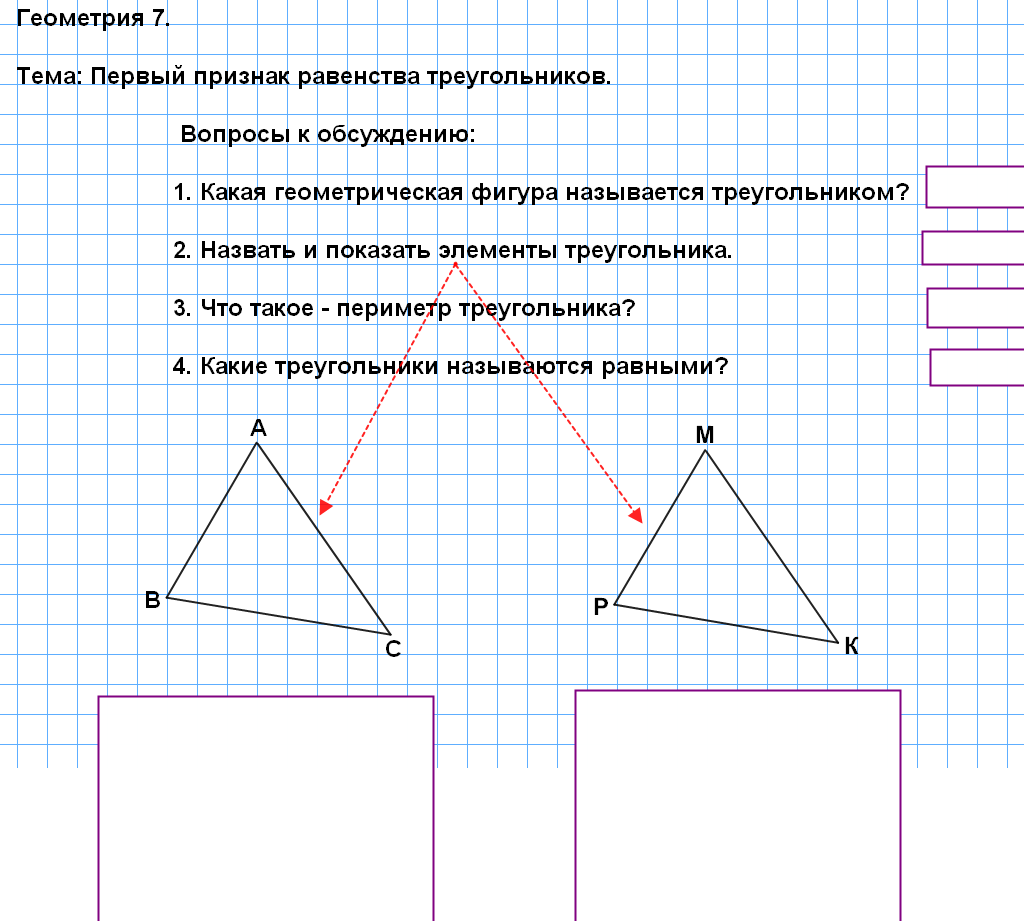
Вопросы для обсуждения: /вопросы помещены на И.Д./
Какая геометрическая фигура называется треугольником?
Назвать и показать элементы треугольника.
Назовите : а) углы ∆ АВС, прилежащие к стороне АВ;
б) углы ∆ МРК, прилежащие к стороне КР;
в) угол ∆ АВС, заключенный между сторонами АВ и СВ;
г) угол ∆ МРК, заключенный между сторонами КР и РМ;
Между какими сторонами в ∆ АВС заключен угол С; в ∆ МРК заключен угол М?
Что такое периметр треугольника?
Какие треугольники называются равными?
Права ли я, утверждая, что треугольники равны, если равны их периметры?
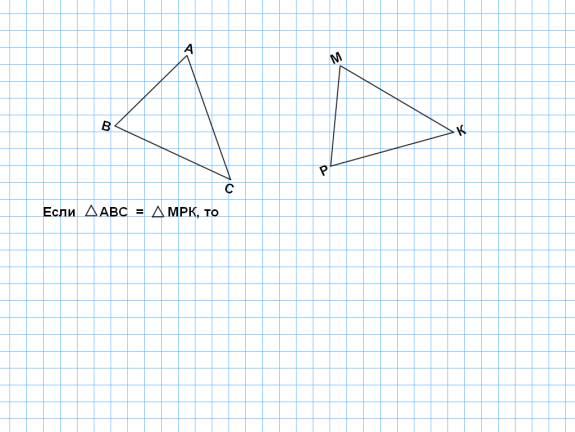
Страница 1 на интерактивной доске. Страница 2 на интерактивной доске.
Практическая работа.
На каждом столе лежит конверт, в котором находятся 6-7 бумажных треугольников. /Работа в парах./
Задание 1. Найти среди них равные треугольники.
Когда поиск закончен, спросить одного из учеников, как он нашел пару равных треугольников. Ученик расскажет, как он накладывал один треугольник на другой.
Задание 2. На карточке 1 найти равные треугольники. Как вы это выполнили?
Задание 3. Есть ли на рисунках /рисунки на И.Д., стр. 3/ равные треугольники?
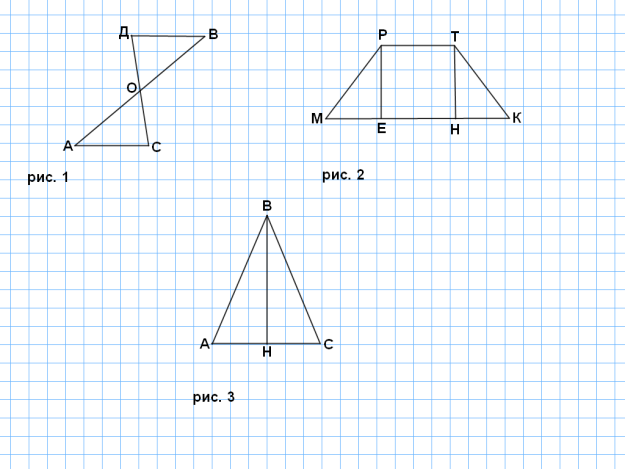
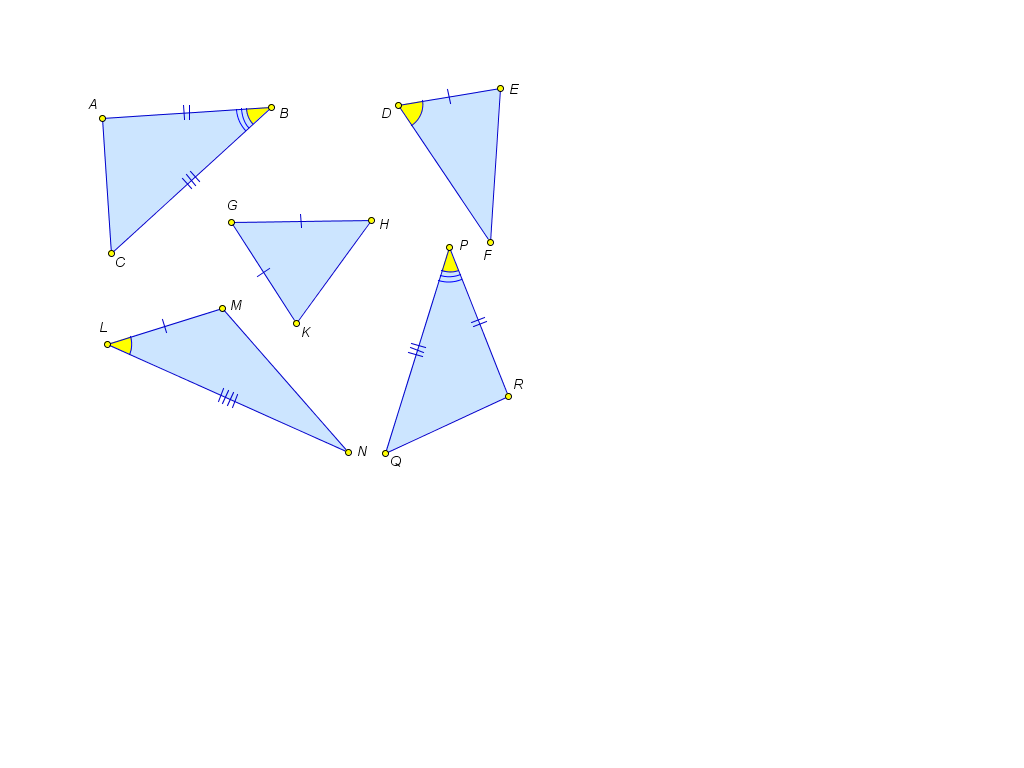
Страница 3 на интерактивной доске. Карточка 1.
Изучение нового материала.
Постановка проблемы.
Вопрос: Можно ли, не совмещая треугольники, не сравнивая их элементы, измерив стороны и углы, сделать вывод об их равенстве?
Задача 1. Равны ли треугольники АВС и АСД? /Рис. 1 на слайде 3 в презентации к уроку/. (Учащиеся обращают внимание на то, что треугольники имеют одну общую сторону).
Задача 2. Равны ли треугольники АВС и АСД? /Рис. 2 на слайде 3 в презентации к уроку/. (Учащиеся обращают внимание на то, что треугольники имеют одну общую сторону и общий угол).
Вопрос: Какое условие можно добавить в задаче для того, чтобы сделать вывод, что данные треугольники равны?
Учитель формулирует теорему – первый признак равенства треугольников.
Предлагает учащимся выделить условие и заключение теоремы. Дает название теоремы.
Вопрос: что такое – признак?
Признак (по В.Далю) – это знак, отличие, все то, почему узнают что–либо. Увидев морозный узор на окне, можно, не выходя из дома, сказать, что на улице холодно. Чтобы узнать, делится ли число 159367285 на 5, не обязательно выполнять деление: можно воспользоваться признаком делимости.
Признак дает возможность устанавливать равенство двух треугольников, не проводя фактического наложения одного из них на другой, а сравнивая только некоторые элементы треугольников.
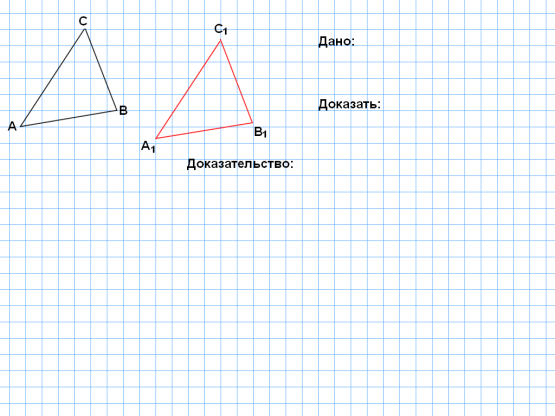
Страница 4 на интерактивной доске.
Работа в тетрадях и на доске. Нарисовать два равных треугольника (по клеточкам), записать, что дано, доказать, доказательство.
Учитель проводит доказательство теоремы, опираясь на знания и умения учащихся.
Дано: ∆ АВС, ∆ А1В1С1, АВ = А1В1, АС = А1С1,  А =
А =  А1.
А1.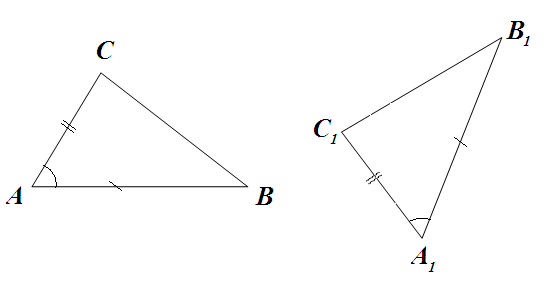
Доказать: ∆ АВС = ∆ А1В1С1. Доказательство:
1. Наложим ∆ АВС на ∆ А1В1С1 так, чтобы
вершина А совместилась с вершиной А1 ;
2. Так как  А =
А =  А1 то сторона АВ пойдет по лучу А1В1, а сторона АС пойдет по лучу А1С1.
А1 то сторона АВ пойдет по лучу А1В1, а сторона АС пойдет по лучу А1С1.
3. Что можно сказать про точки В и С?
Так как АС = А1С1, то точка С совпадает с точкой С1. Так как АВ = А1В1, то точка В совпадет с точкой В1.
Т.е. стороны треугольников АС и А1С1. АВ и А1В1 совместятся.
Следовательно сторона ВС совпадет со стороной В1С1.. Почему?
Итак, треугольники полностью совместятся, значит, они равны согласно определения. Теорема доказана.
4. Первичное закрепление изученного.
Устное решение задач по готовым чертежам. /стр. 3 на И.Д./
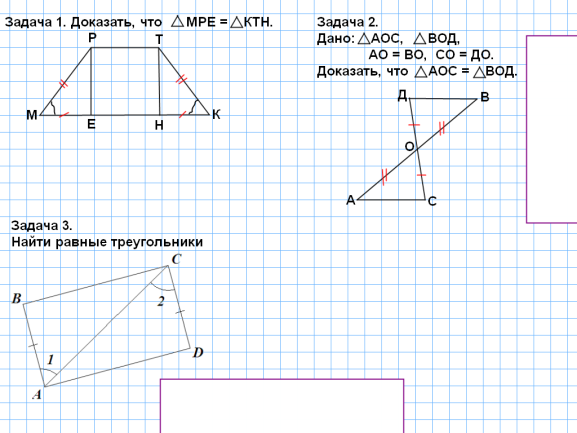
Страница 5 на интерактивной доске.
Итог урока.
Какую тайну о треугольниках вы сегодня узнали?
Что такое теорема?
Чтобы сделать вывод, что данные треугольники равны, сколько пар соответственно равных элементов необходимо найти?
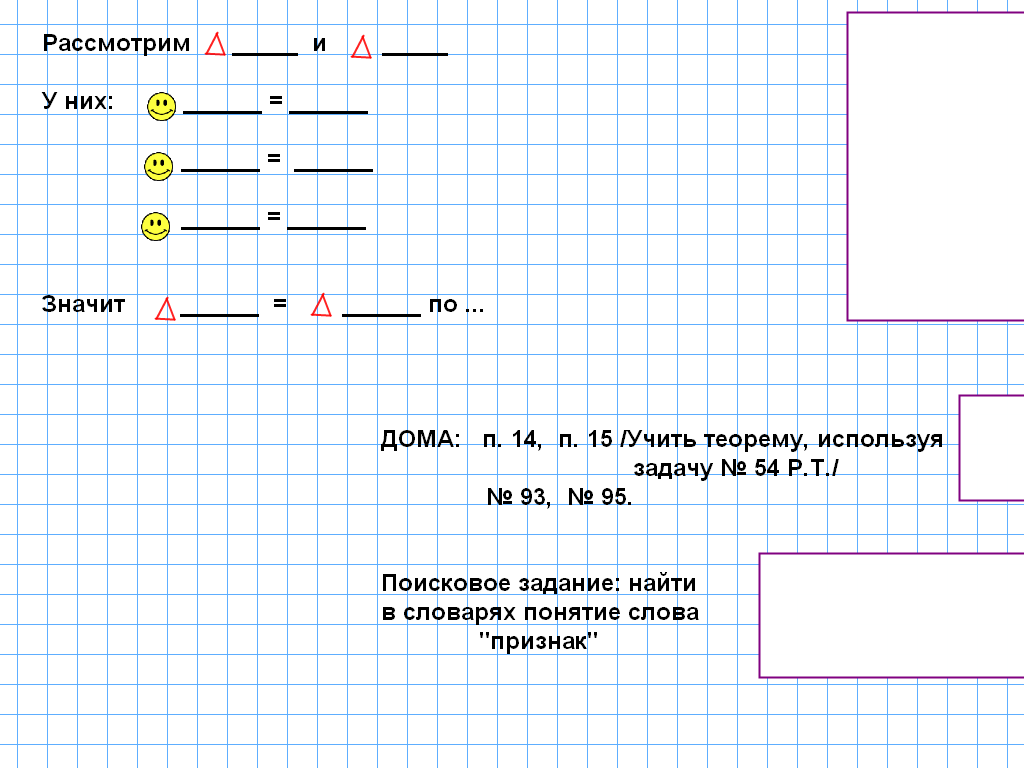
Страница 5 на интерактивной доске.
Домашнее задание: п. 14, п. 15, задачи № 93, № 95. Учить теорему, используя задачу № 54 из рабочей тетради.
Творческое задание: найти понятие слова «признак» по другим словарям.

 Получите свидетельство
Получите свидетельство Вход
Вход












 План конспект уроа по геометрии 7 класса по теме "Признак равенства треугольников" (318.9 KB)
План конспект уроа по геометрии 7 класса по теме "Признак равенства треугольников" (318.9 KB)
 0
0 1258
1258 110
110 Нравится
0
Нравится
0



