План-конспект открытого урока по элементарной математики

План-конспект открытого урока по элементарной математики

Дата: 19.11.2010г.

Группа: 2 курс группа «А»

Аудитория: 29

Учебное время: 3 часа

Тема: Действия над комплексными числами в тригонометрической форме.

Цель: закреплять понятие «комплексное число», совершенствовать вычислительные навыки в решении упражнений с комплексными числами в алгебраической форме, учиться выполнять простейшие действия с комплексными числами в тригонометрической форме; развивать математическое мышление, память, внимание, познавательный интерес; воспитывать интерес к предмету.

Оборудование: ПК, учебный фильм, чертёжные инструменты, тексты самостоятельной работы

Ход урока:

1. Организационное начало.

1. Приветствие.

• Здравствуйте, тихо присаживайтесь. Итак, урок элементарной математики.

1. Психологический настрой.

- Сегодня на урок к нам пришли гости. Я предлагаю нам с вами поработать очень хорошо и показать все наши знания по предмету, умение грамотно и логично выстраивать свои устные и письменные ответы.

1. Проверка готовности к уроку.

- Проверьте, всё ли у вас готово к началу урока: тетрадь, ручки, карандаши и линейка. Всё лишнее уберите со столов.

1. Повторительно-обучающая работа.

1. Сообщение темы и цели урока.

- Прочитаем эпиграф к нашему сегодняшнему уроку (чтение эпиграфа).

-Итак, на предыдущих уроках мы с вами уже познакомились с историей появления понятия «комплексное число»; вспоминали учёных, занимавшихся с данным классом чисел; рассмотрели основные действия над комплексными числами в алгебраической и в тригонометрической формах. А сегодня, в течение трёх часов элементарной математики, мы с вами продолжим работу над понятием «комплексное число». На первом занятии мы с вами вспомним основные тезисы по теме урока, будем решать упражнения с комплексными числами в алгебраической и тригонометрической формах. На втором часу выполним самостоятельную работу по действиям с комплексными числами в алгебраической и тригонометрической формах; а на последнем занятии рассмотрим ещё один вид действий, который можно производить с комплексными числами – это извлечение квадратного корня из комплексного числа. И, я надеюсь, вы ещё раз убедитесь, что комплексные числа действительно получают более и более широкое распространение.

1. Фронтальный опрос.

- Итак, вспомним, как же в математическую практику пришли понятия «мнимая единица» и «комплексное число»? (Термин “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа i (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово «комплекс» (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. образующих единое целое.)

- Какие русские учёные занимались вопросом теории функций комплексного переменного? (Н. И. Мусхелишвили занимался ее применениями к теории упругости;М. В. Келдыш и М. А. Лаврентьев – к аэро- и гидродинамике; Н. Н. Богомолов и В. С. Владимиров – к проблемам квантовой теории поля.)

- Так что же такое «комплексное число»? (Комплексным числом называется число вида a+jb , где a, b − некоторые действительные числа, а j− мнимая единица.)

- Каким символом обозначается множество комплексных чисел? (С)

- Вспомним, сколько всего классов или множеств чисел мы с вами вспомнили на наших занятиях? (6)

- Как они располагаются по отношению друг к другу? Какой класс самый маленький, а какой самый большой? (N, Z, Q, I, R, C)

- Вы сказали, что комплексное число обозначается как z=a+bi. Что же такое в данной записи комплексного числа представляет собой первое слагаемое, а что второе? (Число a называется действительной частью комплексного числа z. Обозначается a=Re z. Число b называется мнимой частью комплексного числа z. Обозначается b=Im z.)

- Хорошо, мне нравится, как вы сегодня работаете на уроке. Скажите мне, пожалуйста, что нам необходимо построить для изображения комплексного числа? (систему координат)

- Как называется вертикальная ось? (мнимая ось)

- Как называется горизонтальная ось? (действительная ось)

- Какие координаты будут изображаться на действительной оси? Мнимой? (а, в)

- А как получить комплексное число в такой системе координат? (найти точку пересечения действительной и мнимой координаты, соединить эту точку с началом координат)

- Проверим, правильно ли вы сформулировали алгоритм изображения комплексного числа на координатной плоскости. Посмотрим на экран.

III. Работа по выработке умений и навыков

1. Сообщение темы и цели урока

- Сегодня на уроке мы с вами продолжи м работу над комплексными числами, а именно продолжим формирование навыка выполнения действий над комплексными числами в тригонометрической форме.

1. Решение упражнений у доски с комментированием.

- Откройте свои рабочие тетради и подпишите в них сегодняшнее число и тему: «Решение упражнений по теме «Комплексные числа».

- Прочитайте задание на экране. (Изобразите комплексные числа)

- Строим у себя в тетрадях данные комплексные числа на одной координатной плоскости. К доске работать над этим заданием идёт…

- Проверьте своё решение с решением у доски. У кого получились другие ответы, поднимите руку.

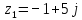
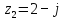
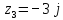
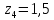
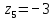
- Прочитаем следующее задание на экране. (Запишите комплексные числа, изображенные на координатной плоскости, в алгебраической форме.)

- Выполним теперь обратную операцию. Сделайте это задание самостоятельно, а затем кто-то один прочитает нам ответы.

- Проверим, что же у вас получилось. Ответы с места нам зачитает…

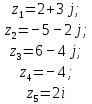
- Поднимите руку, у кого получились другие ответы.

- Молодцы, я вижу, что и с этим заданием вы справились достаточно хорошо.

1. Устное решение упражнений.

- Посмотрим, какое же следующее задание нам предстоит выполнить. Устно посчитаем, какой же из предложенных ответов нам подходит больше всего. Подумайте самостоятельно.

- Кто готов ответить на вопрос данного упражнения? Почему? (4)

- Молодцы, я вижу, что в изображении комплексных чисел у нас неплохие знания, и данный материал вы усвоили достаточно хорошо.

1. Фронтальный опрос.

- Какое число называется противоположным комплексному числу? (Комплексное число -z=-a-bi называется противоположным комплексному числу z=a+bi)

- Если комплексное число располагается в первой координатной четверти, то в какой четверти будет располагаться ему противоположное и почему? (3)

- Какие комплексные числа называются сопряжёнными? (Комплексное число z=a-bi называется противоположным комплексному числу z=a+bi)

- В какой координатной четверти будет располагать сопряжённое данному и почему? (4)

5. Решение упражнений у доски с комментированием.

- Прочитаем следующее задание на слайде. (Запишите числа, сопряженные данным)

-Выполним его самостоятельно в тетрадях и у доски. К доске идёт…

- Посмотрите внимательно на доску. Поднимите руку, у кого получились другие ответы.

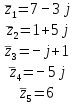
- Сверьте теперь каждый своё решение с правильным на экране.

- Поднимите руку, кто не допустил ни одной ошибки? Одну? Две?

- Те, у кого получилось в решении более двух ошибок, я думаю, лучше выучат данную тему и подготовятся к следующему занятию. А у кого нет ошибок или всего лишь одна молодцы.

6. Устное решение упражнений.

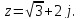- Выполним следующее упражнение со слайда устно. Прочитайте задание про себя. (Какое из данных чисел является сопряженным для числа )

- Кто мне скажет, какой из четырёх вариантов правильный и почему. (в)

- Проверим, правы ли вы. Посмотрим на слайд. Итак, правильным оказался вариант под буквой в). Молодцы, все кто в своих рассуждениях пришёл к такому же выводу.

7. Фронтальный опрос.

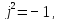- Ещё один большой раздел из всей темы комплексные числа, который мы с вами изучили – это степени мнимой единицы. Итак, по определению, чему же равняется i²? ( )

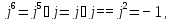
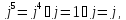
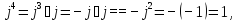
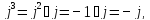- Зная, что i²=1, как узнать, чему равно i³? i⁴? i⁵? (

)

- Хорошо, я вижу, что это вы усвоили хорошо.

8. Запись правила под диктовку.

- А как же быть, если нам необходимо вычислить, например, i¹⁶? Ведь подобные вычисления, как вы видите, довольно громоздки и требуют больших временных затрат. Для этого, мы с вами запишем формулу или алгоритм для вычисления мнимой единицы в степени m.

- Подпишите в своих тетрадях подзаголовок: формула для вычисления мнимой единицы в степени m. Смотрим на экран и записываем формулу к себе в тетради, обводим её обязательно в цветную рамочку, как любое правило или определении.

( 1) Если показатель степени m при j делится на 4 без остатка, то

1. Если при делении показателя степени m при j на 4 получается остаток 1, то

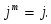
2. Если при делении показателя степени m при j на 4 получается остаток 2, то

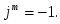
3. Если при делении показателя m при j на 4 получается остаток 3, то )

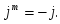9. Решение упражнений у доски с комментированием.

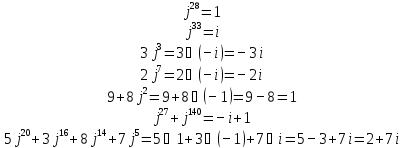- Выполним у доски с комментирование следующее задание и проверим, насколько хорошо мы с вами умеем пользоваться данной формулой. К доске идёт…

- Итак, хорошо, с задание справились. Но я думаю, что данный алгоритм нам с вами нужно будет ещё немного подучить и выполнить больше упражнений такого плана.

10. Фронтальный опрос.

- Следующий момент, который нам с вами обязательно нужно вспомнить – это модуль комплексного числа.

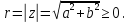
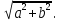
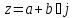- Что же мы с вами называем модулем комплексного числа? (Модулем комплексного числа называется действительное число )

- Как обозначается модуль комплексного числа? ( )

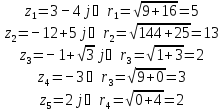- Устно по цепочке посчитаем, следующие примеры на слайде.

- Хорошо, молодцы. Что же называется аргументом комплексного числа? (Угол α, между положительным направлением действительной оси и вектором ОМ называется аргументом комплексного числа )

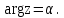- Как обозначается аргумент комплексного числа? ( )

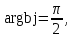
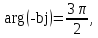
- Вспомним, какие частные случаи мы с вами рассматривали? (

)

- Устно выполним следующие задания на слайде.

- Мне очень понравилось, как вы отвечали на все мои вопросы и решали предложенные вам задания. Я надеюсь, что и самостоятельную работу вы выполните столь же хорошо.

11. Самостоятельная работа по вариантам.

- Дежурные, раздайте, пожалуйста, на столы листы для самостоятельной работы. Уберите всё лишнее со стола и послушайте меня внимательно. Сейчас каждый получит вот такой лист с заданиями по вариантам. Каждый на своём рабочем листе подпишет свою фамилию и номер варианта, как это показано на листах с заданиями, а затем может приступать к выполнению заданий. Выполнять задания можно в любом порядке, время на самостоятельную работу до конца урока. У кого есть ко мне вопросы, задавайте их сейчас.

- Тогда я раздаю задания, и мы приступаем к работе (выполнение самостоятельной работы).

1 вариант

1. Запишите и постройте на координатной плоскости комплексное число, сопряжённое с данным: 1+i;

-3+4i.

1. Решите уравнение: z²+6z+13=0;

16z²-32z+17=0.

1. Найдите полярные координаты точки М: М(3; 4),

М(-1; ).

2 вариант

1. Запишите и постройте на координатной плоскости комплексное число, сопряжённое с данным: 2+3i;

-7-5i.

1. Решите уравнение: z²+2z+17=0;

9z²-12z+5=0.

1. Найдите полярные координаты точки М: М(-12; 5),

М(-3;4).

- Сдайте, пожалуйста, листы с заданиями и ваши решения.

IV. Итог урока

- Чему мы с вами учились на уроке?

- Что нового вы для себя узнали?

- Какие задания вызвали у вас наибольшие затруднения?

- Какие математические термины сегодня на уроке мы с вами вспоминали?

- Отметки за работу на уроке получают…

V. Задавание на дом.