Ямало-Ненецкий автономный округ
Департамент образования Администрации города Ноябрьска
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 9»
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОД НОЯБРЬСК
Педагогический проект
«Построение модели адаптивной среды обучения для совершенствования математического образования школьников в условиях реализации ФГОС»
Автор проекта:
Мамохина Елена Александровна,
учитель математики
высшей категории
МБОУ СОШ № 9
г. Ноябрьск
2016-2021 г
Паспорт проекта
| Полное наименование проекта | Построение модели адаптивной среды обучения для совершенствования математического образования школьников в условиях реализации ФГОС |
| Сроки реализации проекта | долгосрочный |
| Автор проекта | Мамохина Елена Александровна |
| Потребители результатов проекта | учащиеся 5-11 классов, педагоги, родители |
| Краткое описание проекта | |
| Актуальность, новизна проекта | Согласно Концепции развития математического образования в Российской Федерации, утвержденной распоряжением Правительства Российской Федерации от 24.12.2013 № 2506-р, качественное математическое образование необходимо каждому для его успешной жизни в современном обществе. Цель Концепции – вывести российское математическое образование на лидирующее положение в мире. Важнейшей задачей математического образования является развитие и воспитание в человеке способности понимать смысл поставленной перед ним задачи, умение правильно, логично рассуждать, усваивать навыки алгоритмического мышления, эвристическое (творческое) мышление; учиться анализировать, отличать гипотезу от факта, схематизировать, отчетливо выражать свои мысли, развивать воображение и интуицию, пространственное представление, способность предвидеть результат и предугадывать пути решения. Эффективность проекта заключается в развитии и совершенствовании математического образования как взаимосвязи структурных элементов: спектра образовательных услуг, содержания математического образования, форм и методов обучения и воспитания, позиций педагогов, условий, которые в совокупности обеспечат формирование математической образованности ученика. Новизна проекта: если организовать работу в соответствии с адаптивной моделью образования, то это позволит каждому ученику адаптироваться к новым социальным условиям жизни,даст возможность каждому участнику образовательного процесса самореализоваться и саморазвиться. |
| Цели проекта | Выявление, создание условий и разработка модели адаптивной развивающей среды для совершенствования математического образования школьников, обеспечение формирования стойкой мотивации каждого ребенка к развитию. |
| Задачи проекта | Изучить научную, методическую литературу и интернет-источники по теме. Проанализировать практический опыт применения современных образовательных технологий в обучении в практике учителя. Выявить педагогические условия применения модели развивающей среды для развития познавательной активности учеников. Освоить интернет-сервисы для создания и применения модели адаптивной развивающей среды. Разработать и апробировать сборник заданий по формированию функциональной грамотности учащихся на уроках математики. Создать условия для самовыражения и самореализации Провести анализ, систематизацию и обобщение результатов, полученных в ходе реализации проекта. Распространить опыт работы на институциональном, региональном и всероссийском уровне среди педагогического сообщества. |
| Содержание проекта | Подготовительный этап – разработка основных направлений деятельности участников проекта (учителей, родителей, учащихся). Основной (деятельностный) - создание учебных предметных ресурсов, внедрение их в учебный процесс. Заключительный – сравнительный качественный анализ развития умений и навыков школьника, создание банка сетевых проектов. Проект направлен на решение проблемы апробации и адаптации новых методик, предполагающих использование ИКТ, на разных этапах урока в условиях школы. Проект является практико-ориентированным, разработан в результате обобщения педагогического опыта, его структура определена логикой инновационной деятельности. |
| Ресурсы, необходимые для выполнения проекта (кадровые, материальные и др.) | Компьютер, доступ в Интернет, электронная доска, проектор. Учителя исполняющие проект; учащиеся 5-11 классов и их родители; облачные сервисы, платформа CORE, образовательные сервисы Web 2.0., YouTube, LearningApps.org, линоит (англ. Linoit), Padlet, генератор ребусов http://rebus1.com, учебные тренажеры, интернет-платформа Thinlink, образовательные квесты Leаrnis. |
| Форма представления результатов проекта | 1.Диссеминация инновационного опыта: семинары, практикумы по сценированию занятий в деятельностных технологиях, участие в профессиональных математических интернет – сообществах. 2.Аналитические материалы по результатам деятельности. |
| Перспективы развития проекта | По окончании проекта деятельность в выбранном направлении планируется продолжить, учитывая положительные и отрицательные характеристики данного проекта. |
Введение 5
Теоретическое обоснование проекта 8
Концепция направления «математическая грамотность» исследования PISA-2021 9
Концепция развития математического образования в Российской Федерации 12
Нормативно-правовое обеспечение проекта 16
Этапы реализации проекта 17
Планируемые результаты работы над проектом: 18
Основные направления реализации проекта 19
I. Разработка учебно-методического сопровождения преподавания математики в 5 – 11 классах 19
II. Создание образовательной среды, способствующей совершенствованию математического образования учащихся 20
III. Развитие творческих способностей учащихся и повышение учебной мотивации посредством внеурочной деятельности 21
IV. Организация исследовательской деятельности учащихся 21
V. Обеспечение психологического сопровождения обучения 22
VI. Организация взаимодействия с родительской общественностью 22
Целевые индикаторы 23
Описание практического опыта 23
Результативность проекта 27
Заключение 30
Литература 32
"Учить надо не мыслям, а мыслить"
Н.Кант
Обоснование актуальности проекта, его новизны, оригинальности.
Согласно Концепции развития математического образования в Российской Федерации, утвержденной распоряжением Правительства Российской Федерации от 24.12.2013 № 2506-р, качественное математическое образование необходимо каждому для его успешной жизни в современном обществе. Цель Концепции – вывести российское математическое образование на лидирующее положение в мире.
В последние годы проводится огромное количество исследований, связанных с проверкой и выявлением качества среднего образования. Связано это с тем, что многие страны не удовлетворены результатами школьного образования.
По результатам анализа Международной программы по оценке образовательных достижений учащихся (PISA), показатели качества российского образования за последние три года несколько снизились. В рейтинге из 79 стран за 2018 год российские школьники оказались на 31-м месте по читательской грамотности (479 баллов из 1000), на 30-м месте по математической грамотности (488 баллов) и на 33-м месте по естественнонаучной грамотности (478 баллов). Об этом говорится в отчете, опубликованном на сайте Федерального института оценки качества образования, выступающего национальным центром проведения PISA в России.
Система математического образования, сложившаяся в России, является прямой наследницей советской системы. Необходимо сохранить ее достоинства и преодолеть серьезные недостатки. Повышение уровня математической образованности сделает более полноценной жизнь россиян в современном обществе, обеспечит потребности в квалифицированных специалистах для наукоемкого и высокотехнологичного производства.
Инновационный проект «Построение модели адаптивной среды обучения для совершенствования математического образования школьников в условиях реализации ФГОС» направлен на решение задач современного образования, реализует новые подходы к формированию современной модели математического образования. Дает возможность математике стать передовой и привлекательной областью знания и деятельности, а получение математических знаний - осознанным и внутренне мотивированным процессом.
Как известно, на развитие школьника влияют три основных фактора: врожденные задатки, среда и деятельность.
Развивающая среда в современной школе формируется в органичном единстве урочной, внеурочной деятельности и дополнительного образования, с учетом максимально вариативной по своему содержанию и способам человеческой деятельности. Универсальный характер математического знания позволяет интегрировать его с любым другим знанием. Благодаря этому открываются метапредметные обобщения, значимые как для формирования целостной математической культуры школьника, так и его общей культуры.
Кризис, вызванный новым опасным коронавирусом, потребовал экстренных мер для снижения рисков распространения инфекции в разных сферах жизни и деятельности людей. В сфере образования в качестве такой меры был выбран экстренный перевод учебного процесса в дистанционную форму с применением технологий электронного обучения. Современный уровень доступности цифровых технологий для большинства населения страны. Благодаря этому условию возможен выбор школьником индивидуальной образовательной траектории в условиях дистанционного, гибридного и смешанного обучения.
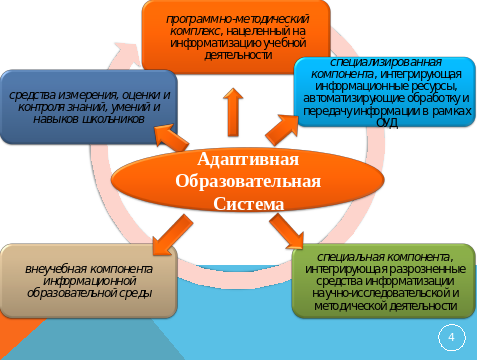
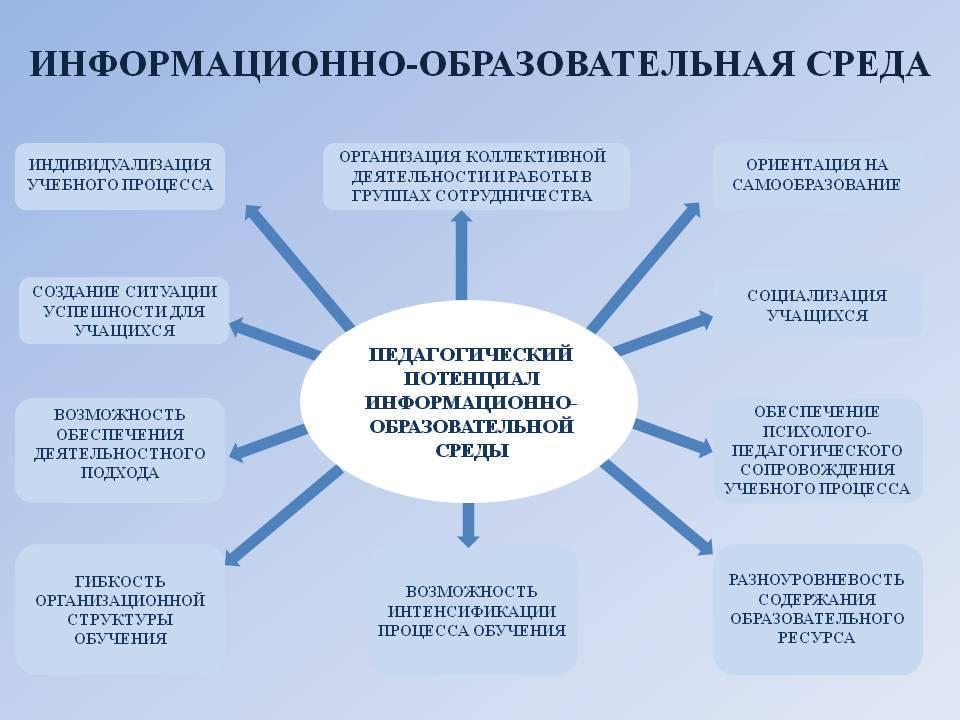
Адаптивная образовательная среда– социально-педагогическая система, приспосабливающаяся к условиям изменяющейся среды, которая стремится, с одной стороны, максимально адаптироваться к личности с ее индивидуальными особенностями, с другой – по возможности гибко реагировать на собственные социокультурные изменения.
(Третьяков П.И., Митин С.Н., Бояринцева Н.И.)
В ФГОС заявлено, что создаваемая развивающая образовательная среда должна способствовать различным видам деятельности школьников: коммуникативной, регулятивной, проектной, учебно-исследовательской, экспериментальной, рефлексивной.
Новизна: использование социальных сервисов для представления конечных продуктов, возможность совместного редактирования, использования медиафайлов, внедрение облачных технологий в нашем образовательном учреждении. Компьютерные сети в обучении также можно применять для совместного использования программных ресурсов, осуществления интерактивного взаимодействия, своевременного получения информации, непрерывного мониторинга качества полученных знаний и т.д.
Причины обращения к проблеме:
пассивность некоторой части учащихся в ходе учебных занятий, во внеурочной деятельности по математике и увеличивающуюся тенденцию потребления знаний в уже готовом виде из-за низкой сформированности исследовательских, креативных, информационно- технологических и коммуникативных умений.
проблема актуализации математического знания через их прикладную направленность в современных условиях, в школе остается значительная часть учащихся, которые по различным причинам не усваивают обязательный минимум содержания образования,
повышается количество учащихся, реальные возможности которых не позволяют им в полной мере осваивать программный минимум по математике, само содержание предмета требует продуктивных способов деятельности учащихся, к чему они не готовы
невозможность в полной мере реализовать свой творческий потенциал в связи с недостаточным использованием новых образовательных технологий в условиях модернизации образования.
Учебная деятельность, направленная в традиционном ее понимании на усвоение учащимися требований базовой школьной программы, не сопряжена в должной степени с творческой деятельностью, способна привести к торможению интеллектуального развития детей. Таким образом, можно сформулировать следующие противоречия между:
- между необходимостью формирования прочных знаний, умений и навыков и большим объемом теоретических сведений, получаемых на уроках математики,
между уровнем знаний по математике и уровнем требований, предъявляемых в заданиях по математике итоговой аттестации;
- между возрастающей практической значимостью школьного курса математики и дефицитом учебного времени;
- потребностями современного общества в инициативных молодых людях и недостаточным уровнем личностной активности у выпускников;
- между желанием дополнительного получения знаний и неумением заниматься самостоятельно;
- между необходимостью получения качественного математического образования и отсутствием внутренней мотивации.
Поиск путей разрешения данных противоречий определяет проблему исследования: как построить учебно-воспитательный процесс, чтобы замотивировать учащихся на оптимальное развитие их интеллектуально-творческого потенциала и достичь наибольших результатов в рамках этой деятельности, не перегружая учебный процесс?
Цель проекта: выявление, создание условий и разработка модели адаптивной развивающей среды для совершенствования математического образования школьников, обеспечение формирования стойкой мотивации каждого ребенка к развитию математического образования через использование современных образовательных технологий.
Задачи проекта:
Изучить научную, методическую литературу и интернет-источники по теме.
Проанализировать практический опыт применения современных образовательных технологий в обучении в практике учителя.
Выявить педагогические условия применения модели развивающей среды для развития познавательной активности учеников.
Освоить интернет-сервисы для создания и применения модели адаптивной развивающей среды.
Разработать и апробировать сборники заданий по формированию функциональной грамотности учащихся на уроках математики.
Создать условия для самовыражения и самореализации обучающихся в области математики на основе индивидуальных образовательных траекторий.
Провести анализ, систематизацию и обобщение результатов, полученных в ходе реализации проекта.
Распространить опыт работы на институциональном, региональном и всероссийском уровне среди педагогического сообщества.
Тип проекта:
По доминирующей деятельности – практико-ориентированный.
По продолжительности – долгосрочный.
Проект рассчитан на учащихся 5-11 классов.
Ожидаемые результаты
Для учащихся:
- получение математических знаний становится осознанным и внутренне мотивированным процессом;
- проявление способности к организации своей деятельности;
- коммуникация с педагогами, сверстниками, общественностью;
- рефлексия собственной деятельности;
-сформированная способность к самоопределению и самоидентификации.
Для педагогического сообщества:
-эффективность реализации ФГОС;
- диагностические материалы по отслеживанию метапредметных результатов;
- повышение профессионального мастерства в решении стратегических задач современного образования;
- профессиональное признание.
Для родительской общественности:
- удовлетворенность качеством образования ребенка;
- возможность принятия активного участия в процессе математического образования и социализации ребенка
- повышение привлекательности и престижа школы
- качественное изменение взаимодействия образовательного учреждения и родителей школьников в решении актуальных задач образования;
- создание информационно-методического банка, доступного для заинтересованных сторон.
Для образовательного учреждения:
- модель образовательного пространства, способствующего развитию математического образования в реализации внедрения федеральных государственных образовательных стандартов;
- стабильно высокое качество образования учащихся по предметам математической направленности;
- основную образовательную программу, обеспечивающую непрерывное математическое образование;
- конкурентоспособность.
Для муниципальной системы образования:
- практические материалы, методические рекомендации по сценированию занятий в деятельностных технологиях;
- диагностические материалы.
Для региональной системы образования:
-образовательное учреждение, предъявляющее и распространяющее опыт работы по развитию математического образования в условиях реализации ФГОС
Теоретическое обоснование проектаМатематическое образование всегда было приоритетом государства, особенно на тех этапах, которые становились ключевыми для его дальнейшего развития. Например, Петр I своим указом в 1701 г. учредил школу математических и навигационных наук. В ней обучали арифметике, геометрии, тригонометрии, черчению, фехтованию, а также морским наукам: навигации, астрономии, географии. Более того, Петр I активно участвовал в составлении учебников: именно он велел ввести в России преподавание геометрии. На первом учебнике геометрии имеются рукописные правки Петра I, которые он сделал под Полтавой. Несколькими веками позже, во времена хрущевской оттепели, возникла идея создания физико-математических школ.
Первые физико-математические школы в Москве, Санкт-Петербурге, Новосибирске открылись в 60-е гг. В 1963 г. принято постановление Совета Министров СССР о создании школ-интернатов в Московском и Новосибирском государственных университетах. В апреле 1984 г. постановлением ЦК КПСС и Совмина СССР было предписано поднять уровень преподавания предметов естественно-математического цикла и т. д. То есть математическому образованию всегда уделялось повышенное внимание. И если мы хотим в настоящее время добиться научного преимущества России, то математическое образование – это та сфера, в которой можно достичь быстрого результата. За счет того, что было создано в советское время в области математического образования и науки, наши математические кадры пользуются глубочайшим уважением в современном научном сообществе. И мы можем вернуть нашей стране передовые позиции в мире, которые у нас были в 70-е гг. XX в. Россия имеет значительный задел в математическом образовании и науке, форсированное развитие этой сферы образования обеспечит прорыв в таких математикоемких стратегических направлениях, как информационные технологии, моделирование в машиностроении, энергетика, экономика, прогнозирование природных и техногенных катастроф, биомедицина.
Концепция направления «математическая грамотность» исследования PISA-2021
Насколько качественное образование получают школьники из разных стран мира? Полезны ли во взрослой жизни знания и навыки, приобретенные в школе? Какие факторы оказывают влияние на уровень образования современных подростков? Почему одни учащиеся показывают высокие, а другие - низкие результаты? Ответить на эти вопросы помогают специальные международные исследования, проводимые среди школьников из разных государств.
Programme for International Student Assessment (PISA) – международная программа по оценке общеобразовательных компетенций учащихся, осуществляемая Организацией экономического сотрудничества и развития (ОЭСР). В соответствии с заявлениями организаторов, цель исследования – оценить, насколько учащиеся старших классов овладели основными знаниями и навыками, способствующими их эффективному функционированию в обществе, и представить количественные результаты, сравнимые на международном уровне. Посредством тестирования подростков, получивших обязательное общее образование, исследование также ставит своей задачей оценить степень развития системы школьного образования в разных странах. Кроме того, в рамках программы изучаются влияющие на достижения школьников факторы, связанные с их семьей, школой, а также существующими вне школы образовательными возможностями.
Концепция по математике PISA-2021
Исследование PISA-2021 будет измерять, насколько эффективно образовательные системы стран готовят учащихся к использованию математики во всех аспектах их личной, общественной и профессиональной жизни.
Концепция объясняет теоретические основы оценивания математической грамотности в исследовании PISA, а также включает официальное определение понятия «математическая грамотность».
В рамках исследования PISA-2021 будет использоваться следующее определение:
Математическая грамотность – это способность человека мыслить математически, формулировать, применять и интерпретировать математику для решения задач в разнообразных практических контекстах. Она включает в себя понятия, процедуры и факты, а также инструменты для описания, объяснения и предсказания явлений. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые должны принимать конструктивные, активные и размышляющие граждане в 21 веке».
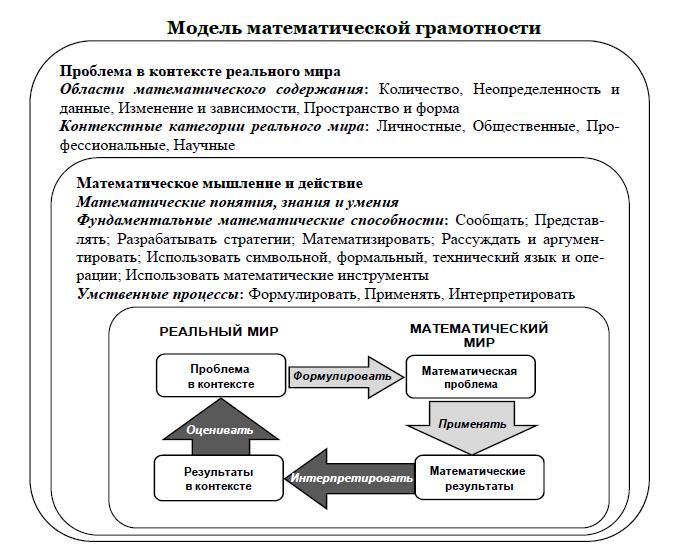
В определении математической грамотности особое внимание уделяется использованию математики для решения практических задач в различных контекстах.
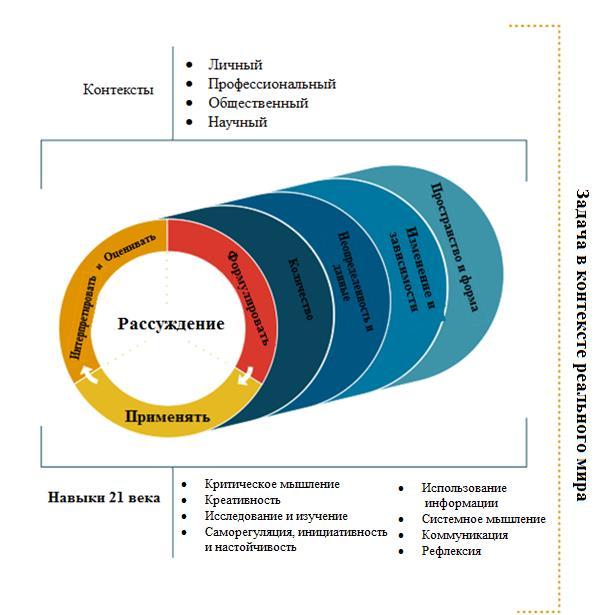
В концепции по математике исследования PISA-2021 ключевой составляющей понятия математическая грамотность является математическое рассуждение.
Способность рассуждать логически и убедительно формулировать аргументы - это навык, который приобретает все большее значение в современном мире. Математика - это наука о четко определенных объектах и понятиях, которые можно анализировать и трансформировать различными способами, используя математическое рассуждение для получения выводов.
В рамках изучения математики учащиеся узнают о том, что, используя правильные рассуждения и предположения, они могут получить результаты, которые заслуживают доверия.
В целом концепция описывает взаимоотношения между математическим рассуждением и тремя процессами цикла по решению задачи (формулирование, применение, интерпретация и оценивание).
В рамках данной концепции математическое содержание разделено по четырем категориям:
Количество
Неопределенность и данные
Изменение и зависимости
Пространство и форма
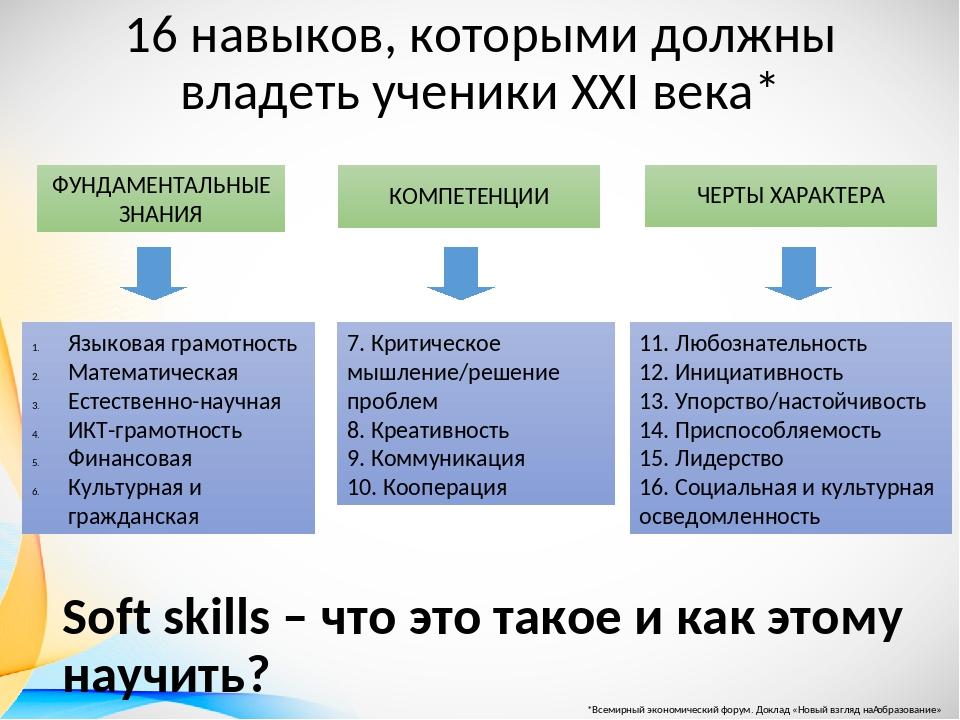
Кроме этого, в концепцию по математике были добавлены восемь навыков 21 века:
Критическое мышление
Креативность
Исследование и изучение
Саморегуляция, инициативность и настойчивость
Использование информации
Системное мышление
Коммуникация
Рефлексия
Исследование PISA проводится циклично: раз в три года. Российская Федерация принимает участие во всех циклах исследования PISA начиная с первого цикла в 2000 году.
Таблица 3. Результаты МО город Ноябрьск и ЯНАО по математической грамотности в сравнении с результатами исследования PISA-2018
| № | Страна | Средний балл | Место страны среди других стран |
| 1 | Китай (4 провинции) | 591 | 1 |
| 2 | Сингапур | 569 | 2 |
| 3 | Макао (Китай) | 558 | 3–4 |
| 4 | Гонконг (Китай) | 551 | 3–4 |
| 5 | Тайвань | 531 | 5–7 |
| … | |||
| 25 | Франция | 495 | 20-29 |
| 26 | Исландия | 495 | 21-29 |
| | МО город Ноябрьск | 495 | |
| … | |||
| | Среднее по ОЭСР | 489 | |
| 30 | Россия | 488 | 27–35 |
| … | |||
| 33 | Люксембург | 483 | 31–36 |
| | Ямало-Ненецкий АО | 483 | |
| 34 | Испания | 481 | 32–37 |
| … | |||
| | Среднее по PISA-2018 | 459 | |
В современном обществе для развития человеку необходимо ставить цели и стремиться к ним, а не работать на достижение и реализацию чужих планов. Но система образования не направлена на формирование и развитие творческих качеств личности учащихся, позволяющих свободно владеть информацией, нетрадиционно и в короткое время решать возникающие проблемы. Учебники, построенные на четких алгоритмах и указаниях к действию, не дают ученикам возможности развивать самостоятельность мышления, быстроту реакции, глубину и гибкость ума. Постоянное следование определенному образцу, игнорирование склонностей и стремлений учащихся приводит лишь к натаскиванию на узкое знание предмета, слепому и необдуманному подражанию чужой идее, нежеланию узнавать и открывать что-то новое. Это противоречие определяет актуальность проблемы развития дивергентного мышления школьников. Дивергентное мышление развивает многосторонний, неоднозначный взгляд на проблему. Но, как показывают результаты тестов международной программы по оценке образовательной деятельности учащихся PISA, проверяющих способность учащихся свободно использовать математические знания в повседневной жизни, наша страна имеет довольно низкие баллы по математической грамотности. Объяснить это можно отсутствием возможности на уроках решать задачи на развитие творческого мышления.
Участие России в программе PISA дает возможность оценить, насколько хорошо подготовлены учащиеся нашей страны относительно школьников из других стран; увидеть сильные и слабые стороны отечественного школьного образования; понять, в каких направлениях совершенствовать российскую систему общего образования.
Результаты по математической грамотности
Р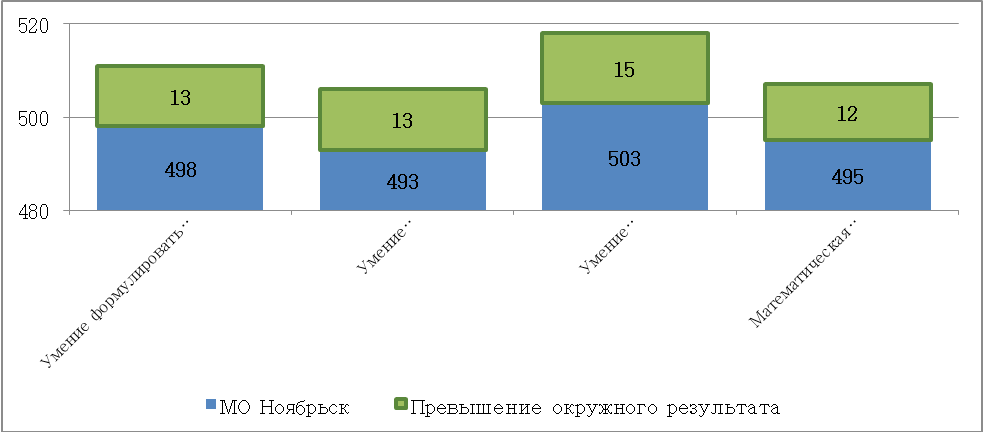 ис. 2. Результаты по математической грамотности
ис. 2. Результаты по математической грамотности
Для того чтобы улучшить позиции наших учащихся в рейтинге PISA, необходимо скорректировать существующие образовательные методики в соответствии со стандартами PISA, сделать их в большей степени ориентированными на практику, не утратив при этом присущую российской школе фундаментальность.
Концепция развития математического образования в Российской Федерации
Математика занимает особое место в науке, культуре и общественной жизни, являясь одной из важнейших составляющих мирового научно-технического прогресса. Изучение математики играет системообразующую роль в образовании, развивая познавательные способности человека, в том числе к логическому мышлению, влияя на преподавание других дисциплин. Качественное математическое образование необходимо каждому для его успешной жизни в современном обществе.
Развитие математического образования обеспечит потребности России в квалифицированных специалистах для наукоемкого и высокотехнологичного производства. Сегодня специалисту, работающему на высокотехнологичном производстве, вряд ли придется вручную производить сложные вычисления, ему едва ли понадобится логарифмическая линейка, но совершенно необходимо видеть систему производственных процессов, понимать принципы работы используемой техники, уметь адаптироваться к постоянной технической и технологической модернизации. Не менее важно умение работать с разнообразной информацией, принимать решения в сфере своей компетенции, взаимодействовать с другими людьми. Математическое образование может быть стартовой площадкой для разработки программ модернизации системы образования в целом и по отдельным учебным предметам: химии, физике, биологии, информатике и др.
Задачами развития математического образования в РФ являются:
модернизация содержания учебных программ математического образования на всех уровнях (с обеспечением их преемственности) исходя из потребностей обучающихся и потребностей общества во всеобщей математической грамотности, в специалистах различного профиля и уровня математической подготовки, в высоких достижениях науки и практики;
обеспечение отсутствия пробелов в базовых знаниях для каждого обучающегося, формирование у участников образовательных отношений установки "нет неспособных к математике детей", обеспечение уверенности в честной и адекватной задачам образования государственной итоговой аттестации, предоставление учителям инструментов диагностики (в том числе автоматизированной) и преодоления индивидуальных трудностей;
обеспечение наличия общедоступных информационных ресурсов, необходимых для реализации учебных программ математического образования, в том числе в электронном формате, инструментов деятельности обучающихся и педагогов, применение современных технологий образовательного процесса;
повышение качества работы преподавателей математики (от педагогических работников общеобразовательных организаций до научно-педагогических работников образовательных организаций высшего образования), усиление механизмов их материальной и социальной поддержки, обеспечение им возможности обращаться к лучшим образцам российского и мирового математического образования, достижениям педагогической науки и современным образовательным технологиям, создание и реализация ими собственных педагогических подходов и авторских программ;
поддержка лидеров математического образования (организаций и отдельных педагогов и ученых, а также структур, формирующихся вокруг лидеров), выявление новых активных лидеров;
обеспечение обучающимся, имеющим высокую мотивацию и проявляющим выдающиеся математические способности, всех условий для развития и применения этих способностей;
популяризация математических знаний и математического образования.
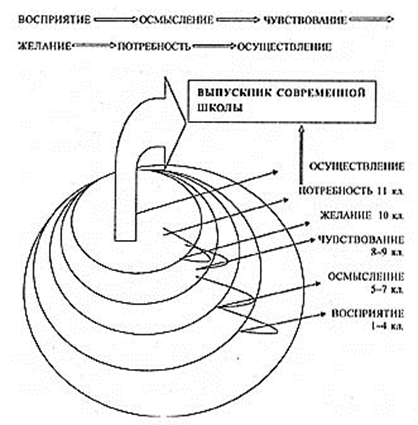
Анализ результатов основного государственного экзамена по школе за последние годы показывает, что качество знаний учащихся 11 классов по математике нестабильно: если в 2017 году качество знаний в 9 кл составляло 36,76%, в 2018 году – 51,86%, а в 2019 году – 48,4% и в 2020 году – 49,9 %. Низкая учебная мотивация школьников связана с недооценкой математического образования. Сложившаяся ситуация негативно влияет также на процесс интеллектуально-творческой самореализации личности школьников и требует изменения подходов в процессе их развития. Чтобы ситуация изменилась, необходимо в образовательном процессе сместить акценты: ученик должен стать полноправным субъектом процесса обучения.
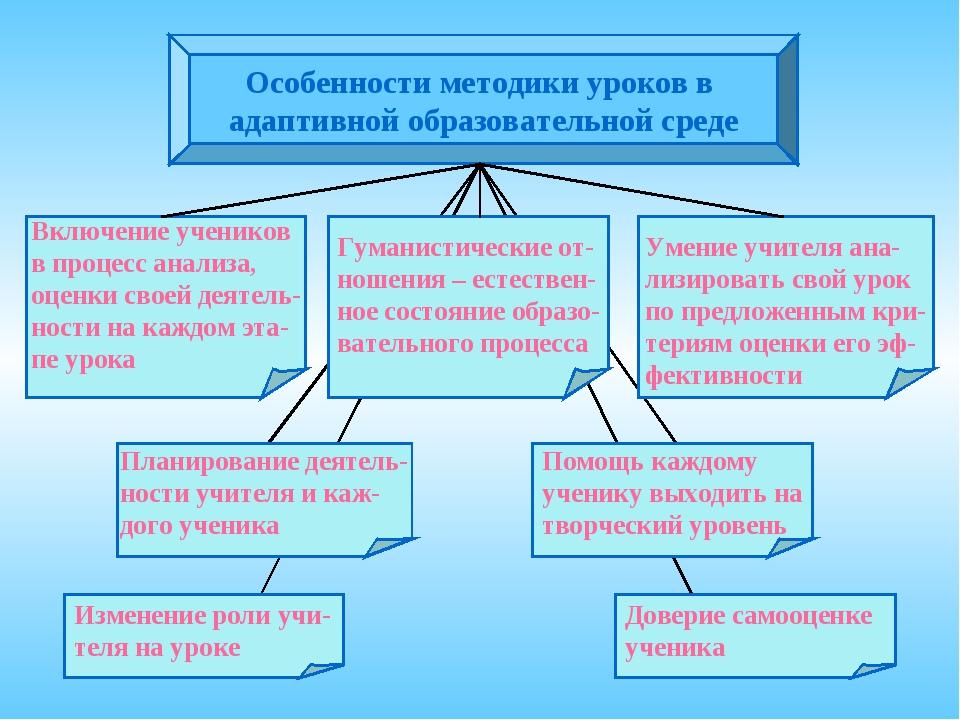
Сегодня на первый план выдвигается самоценность личности подрастающего человека, независимо от особенностей его развития и уровня здоровья. Именно идеи гуманизации привели к появлению в Законе об образовании положения о праве ребёнка и его родителей самостоятельно определять форму получения образования и образовательное учреждение. Они же легли в основу появления в России нового типа образовательных учреждений – школ адаптивного типа. Один из авторов модели школы адаптивного типа – Е.Я. Ямбург утверждал, что в образовательном учреждении должны быть созданы условия для успешного обучения любого ребёнка в соответствии с его способностями, познавательными возможностями, интересами. И одарённые дети, и дети с ограниченными возможностями здоровья, так же как и дети с нормативным развитием - все должны иметь возможность получить образование соответствующего уровня. Решение этой непростой задачи связано, в частности, с созданием в общеобразовательном учреждении особой образовательной среды, которая соответствовала бы различным образовательным потребностям детей. В отношении детей с ограниченными возможностями здоровья можно говорить о необходимости создания в школе единой коррекционно-развивающей среды.
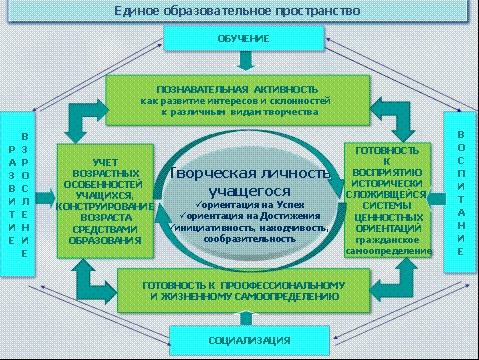
Адаптивной называется образовательная система, способная каждому ученику помочь достичь оптимального уровня интеллектуального развития в соответствии с его природными задатками и способностями.
Важнейший компонент адаптации – согласование самооценок и притязаний с возможностями ученика и с реальностью социальной среды.
«Творчество – это процесс создания человеком объективно или субъективно качественного нового посредством специфических интеллектуальных процедур, которые нельзя представить как точно описываемые и строго регулируемые системы операций или действий». (И.Я. Лернер)
Федеральный государственный образовательный стандарт второго поколения, вступивший в силу с 2011 года, акцентирует внимание на работу по развитию интеллектуально-творческого потенциала в школе. Основными составляющими опыта учебно-творческой деятельности, формирующегося в процессе образования и направленного на развитие нестандартного мышления учащегося, являются:
Самостоятельное осуществление переноса знаний и умений в новую ситуацию.
Обнаружение новой проблемы в стандартной ситуации.
Установление целостной структуры объекта.
Видение новой функции объекта.
Разработка и учет альтернатив при решении проблемы.
Комбинирование и преобразование ранее известных способов деятельности при решении новой проблемы.
К внутренней мотивации относятся радость, удовлетворение от решенной проблемы. Внешняя мотивация, то есть мотивация через вознаграждение, хотя и ведет к определенным успехам, но быстро иссякает, если отсутствует внутренняя мотивация. Исследования среди школьников показывают, что достижения при решении творческих задач оказывались хуже, если они были мотивированы только внешне, через вознаграждение.
Образовательно-воспитательная среда, ориентирующая на развитие творческого потенциала каждого учащегося, создается с опорой на следующие принципы:
принцип адаптивности, т.е. создание среды, которая, с одной стороны, максимально адаптирована к учащимся с их индивидуальными особенностями, а с другой – может гибко реагировать на социально-культурные изменения среды;
принцип развития, предполагающий создание каждому учащемуся условий для полной реализации своих способностей;
принцип психологической комфортности, нацеленный на снятие всех стрессообразующих факторов учебного процесса, создание раскованной, стимулирующей творческую активность атмосферы;
принцип смыслового отношения к миру, требующий не абстрактного познания и отношения к миру, а собственных, осознанных знаний об окружающем мире;
принцип ориентировочной функции знаний, требующий от школы, «не навязывать учащемуся созданного взрослыми мира, но помогать ему преобразовывать мыслью непосредственно очевидный чувственный мир». (П.П. Блонский).
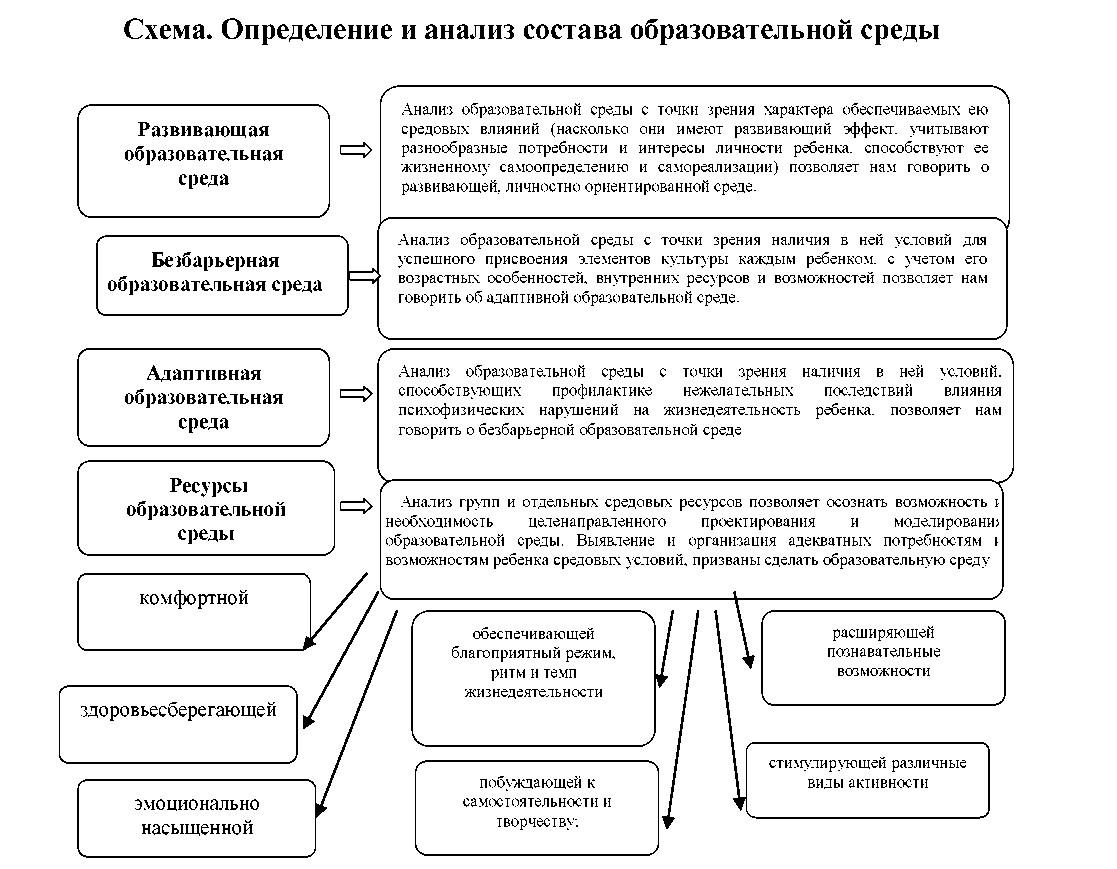
Нормативно-правовое обеспечение проекта
Федеральный закон «Об образовании в Российской федерации»
Концепции Федеральной целевой программы развития образования на 2016 – 2020 годы, утвержденная распоряжением Правительства РФ от 29.12.2004 № 2765-р
Концепция развития математического образования в Российской Федерации, утвержденная распоряжением Правильства РФ от 24 декабря 2013г № 2506-р
Федеральный государственный образовательный стандарт основного общего образования, утвержденный приказом Министерства образования и науки РФ от 17 декабря 2010 года
Основная образовательная программа основного общего образования МАОУ СОШ №9 г. Ноябрьска.
Этапы реализации проекта
| Проблемно-поисковый этап (2015 – 2016) | определение цели, проблемы исследования научно-теоретическое обоснование проблемы и путей ее решения; привлечение психологической службы школы, родительской общественности к работе над проектом. |
| Теоретико-методологический этап (2016 - 2019) | мониторинговые уровня исследования математического образования учащихся; психолого-педагогическая диагностика креативности; составление индивидуальных образовательных маршрутов организация участия школьников в различных формах внеурочной деятельности; охват учащихся элективными курсами. |
| Опытно-практический этап (2016 - 2019) | разработка учебных заданий; разработка модели организации работы по развитию математическх способностей учащихся реализация плана практической деятельности; проведение диагностических исследований.
|
| Контрольно- обобщающий этап (2019 - 2021) | обобщение статистической информации мониторинг успешности реализации проекта подведение итогов реализации проекта обработка результатов исследований; распространение результатов проекта;
|
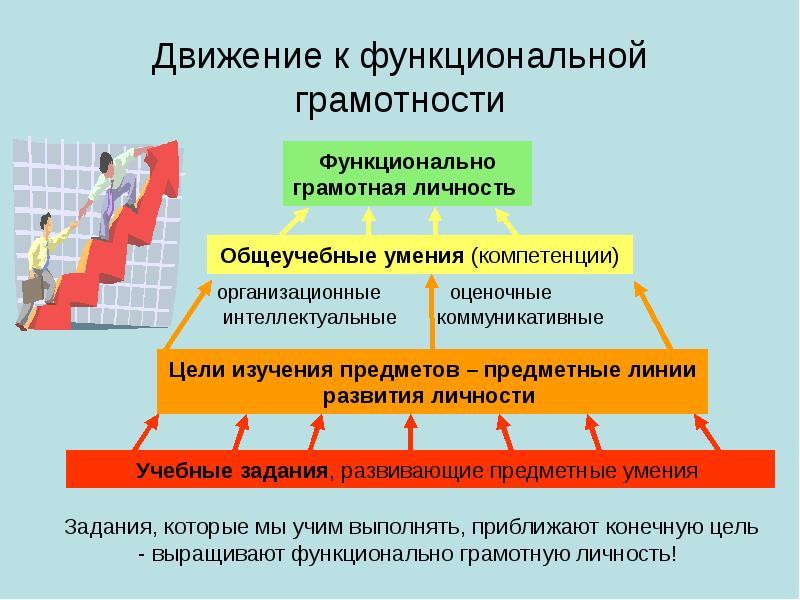
Планируемые результаты работы над проектом:
выявление и развитие у учащихся математических способностей;
формирование стойкого интереса к математике;
повышение и углубление уровня базовой математической подготовки в классе;
повышение интереса к изучению элективных курсов;
повышение результативности участия учащихся в предметных олимпиадах, конкурсах различного уровня;
воспитание профессиональных качеств, любви к исследовательской деятельности, самостоятельности в поиске решений, привитие навыков исследовательской работы;
повышение уровня преподавания математики, внедрение в учебно-воспитательный процесс современных приемов и методов обучения, инновационных технологий;
повышение профессионального уровня педагога.
Основные направления реализации проекта
Разработка учебно-методического сопровождения преподавания математики в 5 – 11 классах
Цель: обновление содержания математического образования
| № | Мероприятие | Срок реализации |
| 1. | Разработка рабочей программы по математике для класса физико- математического профиля (10-11 классы) | Ежегодно до 01.09 |
| 2. | Разработка программы внеурочной деятельности поматематике «Метод рационализации при решении уравнений и неравенств» для 10 класса Разработка программы внеурочной деятельности «Проектная мастерская «Пирамида» для 8 класса. | До 01.09.2019 |
| 3. | Разработка программ элективных курсов: «Решение нестандартных задач» 8 кл. «Решение нестандартных задач» 9 кл. «Применение функций при решении уравнений и неравенств» 10-11кл. «Метод рационализации» 10-11кл | До 01.09.2017 До 01.09.2018 До 01.09.2019 До 01.09.2020
|
| 4. | Создание банка электронно-образовательных ресурсов по математике: дистанционные уроки на интернет платформах CORE и GOOGLE; тесты программированного контроля; сборник ссылок на видеоуроки; образовательные квесты на платформе Learnis; учебные викторины на платформе Cahoot; образцы тестового международного тестирования PISA и TIMS; тренажеры для решения практико-ориентированных задач; полезные ссылки для подготовки к ГИА. | Постоянно |
| 5. | Расширение и углубление содержания математического образования за счет дополнительных часов школьного компонента: теоретико-множественная линия; вероятностно-статистическая линия; историко-культурная линия; вопросы теории делимости; уравнения и системы уравнений с модулями и параметрами и т.п. | Постоянно |
Создание образовательной среды, способствующей совершенствованию математического образования учащихся
Цель: повышение и углубление уровня базового математического образования в классах с углубленным изучением математики
| № | Мероприятие | Срок реализации |
| 1. | Повышение уровня преподавания математики через внедрение в учебно-воспитательный процесс современных образовательных технологий: интерактивные технологии; адаптивные технологии; технологии группового обучения; технология критического мышления; информационно-коммуникационные технологии; технология создания ситуации успеха; игровые технологии; ролевые и деловые игры, тренинги; технология проектного обучения; технология проблемного обучения и пр. | Постоянно |
| 2. | Применение метода укрупления дидактических единиц | Постоянно |
| 3. | Развитие творческой активности учащихся на уроках посредством: обучения умениям самостоятельной деятельности: целеполаганию, планированию, самоконтролю, самоанализу; организация коллективной творческой деятельности (учебные проекты); создание мотивационной заинтересованности в творческом процессе; использование на уроках наглядного моделирования. | Постоянно |
| 4. | Системный мониторинг качества математического образования: входной контроль; текущий контроль; итоговый контроль | Ежегодно Сентябрь Декабрь Май |
| 5. | Составление индивидуальных образовательных маршрутов для детей с ОВЗ, для слабоуспевающих учащихся и для творчески работающих учащихся | По необходимости |
| 6. | Охват учащихся элективными курсами вне программных требований: «Конструирование. Начальная геометрия» 5 кл. «Практикум по решению уравнений и неравенств» 6 кл. «Практикум по решению уравнений и неравенств» 7 кл. «Практикум по решению уравнений и неравенств» 8 кл. «Практикум по решению уравнений и неравенств» 9 кл. | Ежегодно |
Развитие творческих способностей учащихся и повышение учебной мотивации посредством внеурочной деятельности
Цель: организация содержательного интеллектуального досуга, направленного на повышение мотивации к изучению предмета и расширению кругозоа учащихся.
| № | Мероприятие | Срок реализации |
| 1. | Участие в школьном этапе всероссийской олимпиады по математике | Ежегодно |
| 2. | Участие в мунициапльном и обласном этапах всероссийскойолимпиады по математике | По возможности |
| 3. | Участие в международном конкурсе по математике «Кенгуру» | Ежегодно |
| 4. | Привлечение детей к организации и проведению недели математики в школе: «Из истории рационального числа» Математический квест «По тропинкам математики» Математический КВН Конкурс «Ребус» среди 6 классов Конкурс «Прикладной математики» для 8 классов; Лекция «Элементы геометрии Лобачевского» для учащихся 10 классов |
2016 – 2017 2017 – 2018 2018 – 2019 2019 – 2020 2020 - 2021 |
| 5. | Единый урок математики | Ежегодно |
| 6. | Участие в разнообразных конкурсах предметной направленности различного уровня | Согласно плана |
| 7. | Создание портфолио личных достижений учащихся | 2015 – 2021 |
| 8. | Участие в дистанционных математических и межпредметных олимпиадах и математических конкурсах на порталах: Меташкола; Учи.RU Бельчонок и т.п. | Постоянно |
Организация исследовательской деятельности учащихся
Цель: создание условий для раскрытия исследовательского потенциала учащихся, привлечение их к исследовательской деятельности
| № | Мероприятие | Срок реализации |
| 1. | Организация экскурсий в высшие учебные заведения г. Екатеринбурга и встреч с преподавателями ВУЗов | Согласно плана профориентации |
| 2. | Организация ученических исследований по трем направлениям: участие в мини-проектах; написание рефератов; проведение лабораторно-практических работ; создание творческих межпредметных проектов проектов. | Постоянно |
| 3. | Участие в школьном конкурсе проектов | Ежегодно |
| 4. | Участие в ученических конференциях на правах зрителей | Постоянно |
| 5. | Участие в научно-практических семинарах, круглых столах, конференціях со своими исследованиями. | Постоянно |
Обеспечение психологического сопровождения обучения
Цель: создание условий для формирования психологично и социально зрелой личности, ориентированной на развитие собственных способностей
| № | Мероприятие | Срок реализации |
| 1. | Диагностика личности ребенка, выявление творческих и интеллектуальных способностей школьников: тест креативности Торренса; тест Гилфорда для изучения творческого мышления; тест для измерения уровня интеллектуального развития Д.Векслера; диагностика внимания с помощью таблиц Шульте; тест интеллектуальной лабильности; методика «Оперативная память»; диагностика профнаклонностей. | Согласно плану работы школьного психолога |
| 2. | Проведение занятий-тренингов по психокоррекции, профилактике умственных и эмоциональных перегрузок | По запросу |
| 3. | Консультирование родителей творчески работающих учащихся по вопросу поддержки детей, профилактике их умственнойи и эмоциональной перегрузки, стрессов | По запросу |
| 4. | Психологические тренинги «Ориентация на правильный выбор профессии». | 8 – 9 классы |
| 5. | Разработка рекомендаций для учащихся, учителей, родителей по вопросу развития творческих, интеллектуальных способностей детей | 2015 – 2016 |
Организация взаимодействия с родительской общественностью
Цель: привлечение родителей к формированию мировоззрения обучающихся, выбору дальнейшей профессиональной траектории
| № | Мероприятие | Срок реализации |
| 1. | Привлечение родителей к организации образовательных экскурсий, в том числе на предприятия, где они работают | Ежегодно на каникулах |
| 2. | Привлечение родителей к организации и проведению мероприятий интеллектуально-познавательной направленности | Согласно плана работы |
| 3. | Встречи с родителями – преподавателями высших учебных заведений на тему «С вас начинается интеллектуальное будущее России» | Согласно плана работы |
| 4. | Цикл встреч с родителями на тему «Как я выбрал свою профессию» | Ежегодно |
Целевые индикаторы
Целевыми индикаторами при условии выполнения пунктов проекта являются:
отсутствие неуспевающих по предмету «математика»;
повышение качества математического образования к 2021 году до 85%;
охват учащихся класса внеурочной деятельностью до 95%;
ежегодное наличие победителей и призеров школьного этапа всероссийской олимпиады по математике;
ежегодное наличие победителей и (или) призеров муниципального этапа всероссийской олимпиады по математике;
средняя оценка по математике при выпуске из 9 класса, подтвержденная на ОГЭ, не ниже «4»;
увеличение числа участников дистанционных математических олимпида до 80%;
охват учащихся класса мероприятиями интеллектуальной направленности до 90%.
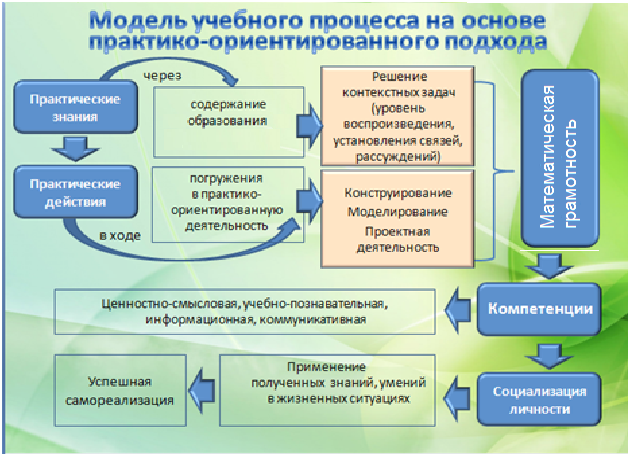
Сегодня образование существует в условиях смены научно-технической эпохи на научно-технологическую, обусловленной решающим значением мобильных знаний и творческих способностей человека. Современный человек начинает относиться к миру не как к абсолютной истине, а как к изменчивому новому, требующему поисковых и исследовательских способов мышления. Такое положение дел формирует преимущественно научно-исследовательский тип российского образования и учитывается в новых образовательных стандартах — ФГОС второго поколения.
Изучение научнаой, методической литературы и интернет-источников
Самостоятельная познавательная деятельность обучаемых организуется, как правило, с помощью дифференцированных учебных заданий (В.В. Гузеев, В.И. Крупич, И.П. Подласый, Р.А. Утеева и др.), в процессе выполнения которых происходит поэтапное усвоение учебной информации (П.Я. Гальперин, В.В. Давыдов, А.Н. Леонтьев, С.Л. Рубинштейн, Н.Ф. Талызина, Д.Б. Эльконин и др.).
Информатизация является одним из значимых средств реализации таких приоритетов новой системы образования как фундаментальность, системность, целостность, ориентация на интересы развития личности. Актуальность внедрения новых информационных технологий и создания единого образовательного и информационного пространства нашла своё отражение в целом ряде научных работ известных учёных (Л.И. Анцыферова, С.Я. Батышев, В.И. Богословский, Г.А. Бордовский, С.М. Вишняков, В.А. Извозчиков, М.В. Кларин, В.А. Козырев, В.В. Лаптев, М.П. Лапчик, А.К. Маркова, Н.Ф. Радионова, И.В. Роберт, А.П. Тряпицына, Р.Р. Фокин и др.).
Проблеме математического моделирования дидактических процессов посвящено достаточно большое число отечественных и зарубежных работ (Р. Аткинсон, Г.Бауэр, Р. Буш, О.Г. Гохман, П.Ф. Зибров, Л.Б. Ительсон, Э. Кротерс, Л.П. Леонтьев, Д.Ллойд, Ф. Мостеллер, С.А. Пиявский, М.И. Потеев, Х. Франк и др.).
Теория развивающегося образования, основанная на системном подходе и опирающаяся на личностно-деятельностную концепцию человека (Б.Г. Ананьев, Д.А. Белухин, П.Я. Гальперин, В.В. Давыдов, А.В. Занков, Э.Ф. Зеер, А.Н. Леонтьев, А.К.Маркова, А.В. Петровский, Л.С. Рубинштейн, В.В. Сериков, Г.Н. Сериков, С.Д. Смирнов, А.В. Хуторской, Д.В. Эльконин И.С. Якиманская и др.);
Современные концептуальные идеи разработки и применения инновационных педагогических технологий, в том числе технологий открытого образования (В.И. Богословский, В.А. Бордовский, Г.А. Бордовский, А.А. Вербицкий, Б.С. Гершунский, В.И. Загвязинский, М.В. Кларин, А.М. Матюшкин, М.И. Махмутов, В.М. Нестеренко, Н.Д. Никандров, Е.С. Полат, Н.Ф. Радионова, Г.К. Селевко, М.П. Сибирская, В.Д. Симоненко, С.Д. Смирнов, Ю.Г. Татур, А.П. Тряпицына, R. Ebel, R. Koller, J.D.Russell, A. Schelton, R. Buhlmann, G. Hofstede, G. Neuer, M. Prokop, U. Tornberg и др.);
Психологическая теория познания и психология памяти и мышления (Р. Арнхейм, Э.Блейлер, Д.Бом, Д. Брунер, Е. Галантер, В.В. Зейгарник, П.И. Зинченко, А.Р. Лурия, Я.Л. Ляудис, А.С. Майданов, Дж. Миллер, Б.П. Невельский, Р.С. Немов, Ж. Пиаже, К. Прибрам, Б.М. Теплов, Д.Н. Узнадзе и др.);
Теория развития мотивации учения (Б.Г. Ананьев, Л.С. Выготский, П.Я. Гальперин, А.П. Леонтьев, А.К. Маркова, А. Маслоу, Ж. Пиаже, В.А. Якунин и др.);
Дифференцированный подход к обучению (В.В. Гузеев, В.И. Крупич, А.К. Маркова, И.П. Подласый, Р.А. Утеева, В.Д. Шадриков, Т.И. Шамова и др.)
Прдуктивное использование новых образовательных технологий
Систематическое повышение профессионального уровня на курсах повышения квалификации, участие в работе вебинаров, школьного и городского методических объединений учителей начальных классов, диссмениция опыта работы, публикация своих работ на образовательных сайтах сети Интернет, участие в профессиональных конкурсах, выступение с предоставлением опыта своей деятельности.
Мастер класс по технологии развития критического мышления. «Как научить составлять кластеры по темам. Геометрия 7 класс». Протокол ШМО от 06.03.2020 №5.
«Представление педагогических практик, ориентированных на формирование и повышение уровня читательской грамотности учащихся» через открытый урок в 9 б классе по теме «Целые уравнения». Приказ №678 –од от 26.11. 2019
Выступление « Реализация ФГОС по геометрии через выбор новой линии учебников издательства Просвещения, Берсенев А. В., Сафонова Н.В. Геометрия 7 класс, протокол №4 от 24.01.20.
Представление проектов на школьном конкурсе. Приказы от 04.04. 2016 г. № 182 -од; от 13.04.207 № 250 –од «Об итогах конкурса проектных работ среди учащихся МБОУ СОШ №9».
Групповая работа и работа в парах на уроках геометрии в 7 классе, при решении задач на исследование и доказательство.
Выступление по теме «Решение задач повышенной сложности по геометрии (задача 26 ОГЭ) исследования, обнаружение закономерностей, доказательство в частных и общем случаях». Протокол от 31.10.19 №2.
Выступление по теме «Формирование метапредметных результатов при решении текстовых задач на уроках математики» на научно-методическом семинаре. Приказ МБОУ СОШ №9 от 11.11.2019 № 638-од.
Запись видеоурока в 7 классе «Решение задач по теме равнобедренный треугольник» https://disk.yandex.ru/i/FtJ6WHEOaYWIQQ
Представление педагогической практики: «Урок на дистанте. Веб-инструменты и сервисы, образовательные технологии, позволяющие обеспечить дистанционное взаимодействие участников образовательного процесса». Протокол ШМО от 05.09.20 №1.
Запись видеоурока в 10 классе «Решение неравенств методом интервалов», с помощью платформы ZOOM https://disk.yandex.ru/i/C4w6vH5AgV6gPg
Мастер класс по созданию тестов по математике на сайте Online Test Pad. Протокол ШМО от 06.03.20 №5
Выступление в рамках 2 регионального Форума учителей математики, физики, географии образовательных организаций ЯНАО: тезисный доклад «Проектная деятельность на уроках математики и во внеурочной деятельности как средство активизации и раскрытия творческого потенциала» (сборник Форума).
Выступление «Школа завтра: гибридному уроку быть!» Макет образовательных курсов для педагогов.
Выступление «Геометрическая задача как инструмент формирования функциональной грамотности».
Выступление «Урок на дистанте. Веб-инструменты и сервисы, образовательные технологии, позволяющие обеспечить дистанционное взаимодействие участников образовательного процесса».
Выступление « Система работы на уроках математики по формированию функциональной грамотности».
Выступление «Реализация ФГОС по геометрии через выбор новой линии учебников издательства Просвещения, Берсенев А. В., Сафонова Н.В. Геометрия 7 класс».
Выступление «Реестр затруднений ОГЭ и ЕГЭ».
Защита проекта «Создание образовательного контента по планиметрии для подготовки к ГИА с помощью конструктора интерактивных уроков CORE» в рамках участия в конкурсе проектов программы развития учителей будущего «NEXT – Педагог», ТюмГУ. г Тобольск.
Выступление «Геометрическая задача как инструмент формирования функциональной грамотности».
Выступление по теме «Формирование метапредметных результатов при решении текстовых задач на уроках математики» на научно-методическом семинаре.
«Представление педагогических практик, ориентированных на формирование и повышение уровня читательской грамотности учащихся» через открытый урок в 9 б классе по теме «Целые уравнения».
По состоянию на конец 2020 года наблюдается следующая ситуация:
стабильная успевамость по математике – на протяжении всех лет обучения составляет 100%;
качество знаний по математике находится в пределах 46,4%– 81,8%%;
всероссийская проверочная работа в 7-х классах. Общая успеваемость 7б-92 %, Качественная успеваемость 7б - 57%;
Всероссийская проверочная работа в 8-х классах. Общая успеваемость 8б-100 %, Качественная успеваемость 7б - 60%;
Мониторинг оценки профессиональной компетентности учителей математики и достижений обучающихся 8-х классов по математике (учащиеся). Общая успеваемость 8а -70%, 8 б-100 %, качественная успеваемость 8а – 40%, 8 б- 73%;
Получили похвальные листы «За особые успехи в учении»
2015/2016 гг. Горякина Надежда, Ленда Юлия, Софяк Анна,
2016/2017 гг. Ленда Юлия, Ледовская Полина, Барышев Михаил, Яловская Анастасия,
2017/2018 гг. Кокоталкина Анна, Ледовская Полина, Салимова Людмила, Барышев Михаил, Яловская Анастасия,
2018/2019 гг. Софья, Мельникова Анастасия, Ташбулатов Дамир, Урусова Анастасия, Ленда Юлия, Кокоталкина Анна, Софяк Анна.
Получили золотую медаль
2017/2018 гг. Яловская Анастасия,
2019/2020гг. Аксёнова Софья, Софяк Анна.
2016-2017 гг. Всероссийская олимпиада школьников по математике, 25 участников, победители – 1, призёр-7, школьный уровень;
2018-2019 гг. Всероссийская олимпиада школьников по математике, 20 участников, победители – 3, призёр-5, школьный уровень;
2018-2019 гг. Всероссийская олимпиада школьников по математике, 3 участника, победители – 3, призёр-1, городской уровень, Аксенова Софья Олеговна 10 кл. как победитель школьного этапа участвовала в муниципальном этапе олимпиады по математике и стала призером;
2019-2020 гг. Всероссийская олимпиада школьников по математике, 27 участников, победители – 2, призёр-6, школьный уровень;
2019 – 2020 гг. Всероссийская олимпиада школьников по математике, 3 участника, победители – 3, призёр-1, городской уровень Филонов Максим 11 кл. как победитель школьного этапа участвовал в муниципальном этапе олимпиады по математике и стал призером;
2019-2020 гг. Международная онлайн-олимпиада «Фоксфорда». Сезон XIV, 14 участников, 3 призера;
2019-2020 гг. XV Международная олимпиада по математике для 1-11 классов. https://mega-talant.com/, 17 участников, 5 призеров;

2019-2020 гг. Международный математический конкурс «Ребус», 16 участников, 14 призеров
2019-2020 гг. Всероссийская онлайн-олимпиада Учи.ру по математике для 5–11 классов Январь–февраль 2020, 16 участников, 9 призеров;
2018-2019 гг. IX Всероссийская дистанционная олимпиада с международным участием Ростконкурс. https://rostkonkurs.ru/, 12 участников, 8 призеров;
2018-2019 гг. Международная онлайн-олимпиада «Фоксфорда». Сезон XI, 20 участников, 3 призера;
Достижения педагога
Участие в конкурсах профессионального мастерства:
2020 г. Сертификат участнику программы развития учителей будущего «Next – Педагог», ТюмГУ и ООО «СИБУР Тобольск»
2020 г. Сертификат отличия 1 степени Международной аттестации профессиональных компетенций по теме «Методика формирования ситуации успеха в учебном процессе».
https://znanio.ru/
2020 г. Сертификат за участие в работе регионального массового мероприятия Хакатон «Ямал – центр образовательного туризма 20.30» https://vk.com/club200481070
2020 г. Диплом за 1 место Всероссийской олимпиады «Педагогическая практика» в номинации «Личностно ориентированный подход в системе основного общего образования. https://pedpractice.ru/
2020 г. Диплом за 1 место Всероссийского тестирования «ТоталТест Август 2020» по теме «Формирование читательской грамотности у обучающихся». https://totaltest.ru/
2019 г. Победитель (2 место) Международного педагогического конкурса "Успешные практики в образовании" Номинация: "Обобщение педагогического опыта" Конкурсная работа: Приемы и способы устранения типичных ошибок на ЕГЭ по математике.
https://evrazio.ru/prinyat-uchastie-v-konkurse/
2019 г. Свидетельство участника 1-го онлайн тура XII Международной профессиональной олимпиады учителей «ПРОФИ -2019» по математике. http://olimphse.tmweb.ru
2018 г. Диплом Всероссийского конкурса профессионального мастерства педагогических работников, приуроченных к 130-летию рождения А.С. Макаренко.
https://www.xn--d1abkefqip0a2f.xn--p1ai/
2018 г. Диплом Всероссийского тестирования педагогов 2018г на портале Удиный урок по теме «Учитель математики в соответствии с требованиями профессионального стандарта и ФГОС»
https://www.xn--d1abkefqip0a2f.xn--p1ai/
2018 г. Свидетельство участника 1-го онлайн тура XI Международной профессиональной олимпиады учителей «ПРОФИ -2018» по математике http://olimphse.tmweb.ru
2018 г. Диплом (2 место) Всероссийского профессионального тестирования «Интерактивные технологии обучения в современном образовательном учреждении». crp.online
2018 г. Победитель (2 место) VI Всероссийского педагогического конкурса «ФГОСОБРазование» в номинации: «Методическая компетентность педагога в соответствии с ФГОС». https://fgosobr.ru/
2018 г. Сертификат отличия II степени по теме «Технология исследовательской деятельности с использованием проблемно-поискового метода обучения, как инструмент реализации ФГОС». https://znanio.ru/
2018 г. Диплом I степени Всероссийского тестирования «ТоталТест Февраль 2018» по теме «Теория и практика преподавания, владение педагогическими технологиями, средствами, методами». https://totaltest.ru/
2017 г. Сертификат участника XII заочного творческого конкурса учителей математики. http://www.mcnmo.ru/oluch/
2016 г. Диплом 1 степени Международной интернет-олипиады по математике «Действия с рациональными числами». https://solncesvet.ru
2016 г. Диплом Всероссийского конкурса «Умната» https://umnata.ru/
Публикация статей, методические материалы на федеральном, региональном, муниципальном уровнях.
Статья «Формирование метапредметных результатов посредством реализации технологии деятельностного метода на уроках математики».
Статья «Методика работы с задачами, способствующими самостоятельному открытию знаний».
Статья «Работа с текстом на уроках математики 5 класс».
Статья «Методика работы с задачами, способствующими самостоятельному открытию знаний».
Статья «Метод рационализации в решении показательных неравенств.11кл».
Публикация Рабочая программа по алгебре 8 класс. ФГОС. по учебнику под редакцией А.Г. Мордкович». Сайт «Учебные презентации».
Диссеминация опыта работы в рамках 2 регионального Форума учителей математики, физики, географии образовательных организаций ЯНАО: тезисный доклад «Проектная деятельность на уроках математики и во внеурочной деятельности как средство активизации и раскрытия творческого потенциала» (сборник Форума).
Выступление на научно-практическом семинаре «Обобщение опыта работы в форме научно-практической конференции «Идеи, достойные распространения» по теме «Система работы по подготовке к государственной итоговой аттестации по математике»
Адаптивная образовательная среда
Интеграция элементов медиаобразования с базовым образованием
Видеоуроки
Арифметический квадратный корень,
Квадратное урававнение,
Площадь трапеции.Решение задач,
Линейная функция.(1),
Линейная функция(2),
Как находить значение тригонометрической функции по тригонометрическому кругу ,
Как решать неравенства методом интервалов.Все опасности ,
Показательная функция ,
Показательные неравенства (1),
Показательные неравенства(2) ,
Способы решения показательных уравнений.
Создание школьного банка электронных образовательных и информационных
ресурсов
Дистанционные уроки
https://sites.google.com/view/distant-matematika/главная-страница
Внеурочные мероприятия
https://sites.google.com/view/vne-urokov/главная-страница
Банк уроков на платформе CORE
Решение уравнений https://coreapp.ai/app/preview/lesson/607299f7910b36249431be3d
Алгебраические выражения https://coreapp.ai/app/preview/lesson/60729a1192cc933ba7461101
Графики функций
https://coreapp.ai/app/preview/lesson/607299d6afe5b96ae92e2193
Теория вероятности https://coreapp.ai/app/preview/lesson/6072994e29a9c754e53427d0
Создание условий для развития креативного медиатворчества и инициативы учащихся
Сборник ссылок на дистанционные конкурсы
https://elenamamohina89.wixsite.com/matematika
Сборник тренажеров по математике
https://sites.google.com/view/trenaqer-matematika/главная-страница
Использование дистанционного информационного обмена
Форум учителя,
https://mamkhina.blogspot.com/
Электронные доски Linoit, Padlet, Jamboard
http://linoit.com/home/canvasesPreferences
Индивидуальная траектория математического развития учащихся
индивидуальный план подготовки ученика к ГИА ,
индивидуальный образовательный маршрут ученика,
карта совершенствования математического образования ученика.
https://elenamamohina89.wixsite.com/matematika
ЗаключениеОдно из важнейших условий обеспечения комфортной и стимулирующей школьной среды - грамотно организованная образовательная среда, её атмосфера и наполнение, поскольку только гармоничная среда способствует становлению личности.
В последнем послании Президента Российской Федерации Путина В.В. к Федеральному Собранию им были четко расставлены акценты приоритетов в образовании: «Нужно переходить и к принципиально новым, в том числе индивидуальным технологиям обучения, уже с ранних лет прививать готовность к изменениям, к творческому поиску, учить работе в команде, что очень важно в современном мире, навыкам жизни в цифровую эпоху».
Современная реформа системы образования ориентирована на развитие личности обучающегося, его способностей к самостоятельной учебной деятельности. Одним из важных направлений деятельности современной школы является такая организация учебного процесса, которая обеспечивает глубокие и прочные знания основ наук, формирует у обучающихся умение самостоятельно мыслить, развивает творчество и инициативу.
Федеральный государственный образовательный стандарт второго поколения, вступивший в силу с 2011 года, акцентирует внимание на работу по развитию интеллектуально-творческого потенциала в школе. В стандартах прописан социальный заказ общества, ориентированный на творческую, активную личность, способную проявить себя в нестандартных условиях, гибко и самостоятельно использовать приобретенные знания в разнообразных жизненных ситуациях. Подтверждение данным словам мы находим в Концепции Федеральной целевой программы развития образования на 2016 – 2020 годы, где одной из задач по реализации новых подходов в образовании является создание условий для личностного развития детей и молодежи, популяризация среди них научно-образовательной и творческой деятельности, выявление талантливой молодежи. В условиях решения этих стратегических задач важнейшими качествами личности становятся инициативность, способность творчески мыслить и находить нестандартные решения, умение выбирать профессиональный путь, готовность обучаться в течение всей жизни».
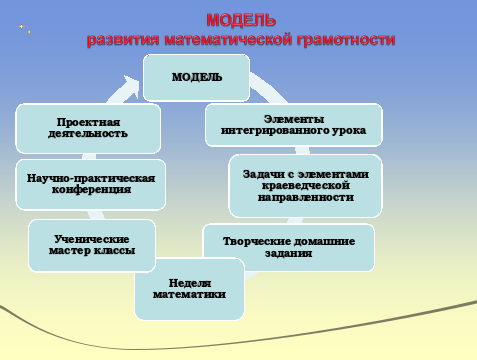
Что же нужно сделать, чтобы ученик мог гибко адаптироваться к меняющимся жизненным ситуациям; видел трудности и искал пути их преодоления, используя современные технологии; мог бы чётко осознавать, где и каким образом приобретённые знания могут быть применены на практике; умел бы грамотно работать с информацией; был коммуникабельным; мог самостоятельно работать над собственным развитием?
Ответом могут послужить слова А. Дистервега: «Плохой учитель преподносит истину, хороший учит её находить».
В сегодняшнем образовательном пространстве все еще преобладающим является подход к обучению, который предполагает усвоение определенного набора знаний. Но современная ситуация требует не только обладания суммой знаний, но и готовности к постоянным изменениям проблемной ситуации, ее условий, а также умением находить оптимальный способ ее решения. Успех разрешения такой ситуации зависит от умения анализировать и прогнозировать в короткие сроки. Эта способность называется креативностью или способностью к творчеству. Креативность – это процесс дивергентного мышления.
На качество знаний ученика влияют не только внешние, но и внутренние факторы: личностные установки на достижение результата и ценностно-мотивационное отношение к обучению, то есть отсутствие у детей мотивации - желания учиться.
Ещё в 14 веке В. Вундт доказал, что при пассивном восприятии готовых понятий появляется чувство страдания, а при активном напряжении, стремлении к определённой цели появляется чувство удовлетворения. В связи с этим традиционная схема: УЧИТЕЛЬ-УЧЕБНИК-УЧЕНИК- должна быть в адаптивной школе заменена на новую: УЧЕНИК-УЧЕБНИК-УЧИТЕЛЬ.
Итак, подводя итоги сказанному, приходим к выводу о том, что создание адаптивной развивающей среды позволяет каждому ребенку найти свое место в жизни, развить свои дарования, реализовать себя.
Фундаментальное ядро содержания общего образования / Рос. акад. Наук, Рос. акад. образования; под ред. В.В.Козлова, А.М.Кондакова. – 4-е изд., дораб. – М. : просвещение, 2011. – 79 с.
Концепция федеральных государственных образовательных стандартов общего образования.
Гилфорд, Дж. Три стороны интеллекта // Психология мышления – М: Прогресс, 1965.
Даринская Л.А. Творческий потенциал учащихся: методология, теория, практика: Монография. – СПб., 2005. – 293 с.
Кулюткин Ю.Н. Изменяющийся мир и проблема развития творческого потенциала личнсти. Ценностно-смысловой анализ. – СПб.: СПбГУПМ, 2001. – 84 с.
Е.Ю. Умярова Психолого – педагогические условия самореализации учащихся в системе дополнительного образования // Научный журнал «Известия Самарского научного центра РАН», т.11, 4(4), 2009. [Электронный ресурс] – режим доступа:http://ssc.smr.ru/izv_2009_4.html, 10,
Ященко И.В., Рослова Л.О., Высоцкий И.Р, Семенов А.В. «Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по математике». Москва, Федеральный институт педагогический измерений.
Егорова, Т. Г. Образовательная среда как педагогический феномен [Электронный ресурс]. – URL: http://shgpi.edu. ru/files/nauka/vestnik/2013/2013-2- 10.pdf (дата обращения: 02.06.2018).
Лепихина С.И. «Формирование и развитие умений смыслового чтения на уроках математики». Педагогическое сообщество «УРОК.РФ»: https://урок.рф
Чернова Е. Н. «Формирование навыков смыслового чтения на уроках математики», 2016 г. Интернет-ресурс: https://multiurok.ru/

 Получите свидетельство
Получите свидетельство Вход
Вход












 Педагогический проект «Построение модели адаптивной среды обучения для со-вершенствования математического образования школьников в условиях реализации ФГОС» (5.91 MB)
Педагогический проект «Построение модели адаптивной среды обучения для со-вершенствования математического образования школьников в условиях реализации ФГОС» (5.91 MB)
 0
0 201
201 11
11 Нравится
0
Нравится
0


