Օժանդակ խնդիրներ հարթաչափությունից

ՕԺԱՆԴԱԿ ԽՆԴԻՐՆԵՐ ՀԱՐԹԱՉԱՓՈՒԹՅՈՒՆԻՑ

Բանալի բառեր - արտագծած և ներգծած շրջանագծեր, արտաքին շոշափում, շառավիղ, պարագիծ, մակերես, ընդհանուր շոշափող:

Գաղտնիք չէ, որ մաթեմատիկական կրթության գերակա նպատակը աշակերտների ինտելեկտուալ զարգացումն է, մտածողության այնպիսի որակների ձևավորումը, որոնք հատուկ են մաթեմատիկական գործունեությանը և անհրաժեշտ են մարդկանց հասարակության մեջ լիարժեք անդամ լինելու համար։ Այդ գործում շատ կարևոր դեր ունի երկրաչափության ուսուցումը դպրոցում։Երկրաչափությունը` որպես երկրաչա-փական պատկերներ ուսումնասիրող գիտություն, հարուստ է պատկերների գեղեցիկ և էֆեկտիվ համադրումներով ու հատկություններով։ Երկրաչափության դպրոցական դասընթացն ընդգրկում է մեծ քանակությամբ խնդիրներ, որոնք լուծվում են որոշակի ալգորիթմներով։

Օրինակ այն խնդիրները, որոնք ամրապնդում են բանաձևերի իմացությունը և զուտ հաշվողական բնույթի են, չեն կարող ապահովել սովորողների ստեղծագործական մտածողության զարգացումը։Իսկ ոչ ստանդարտ խնդիրը չի կարող լուծվել նախապես հայտնի ալգորիթմով, անհրաժեշտութուն է առաջանում սկսել լուծման որոնումը, որը և ենթադրում է մտածողության զարգացում։ Խնդրի լուծմամբ պայմանավորված մտածողության լարվածությունը և հայտնագործության բերկրանքը հադիսանում են ստեղծագործական ուսուցման զգայական գործոնները։

Աշակերտի մոտ հետաքրքրություն է առաջանում ինքնուրույն փնտրելու և գտնելու խնդրի լուծումը։ Դրա համար աշակերտը պետք է ունենա տեսական գիտելիքների հարուստ պաշար և կարողանա արդեն լուծված խնդիրներում հայտնաբերել կարևոր փաստեր և դրանք ընդհանրացնել։ Երկրաչափական փաստերը, որոնք կարելի է ձևակերպել որպես թեորեմներ,անվերջ են: Դրանցից շատերը հանդես են գալիս երկրաչափության դասագրքերում որպես ապացույցի խնդիրներ: Վերջիններիս իմացությունը և կիրառումը մի շարք խնդիրների լուծում դարձնում է ավելի արդյունավետ և արագ: Դիտարկենք մի քանի այդպիսի օրինակներ:

Խնդիր 1.Ապացուցել, որ արտաքին շոշափում ունեցող R₁,R₂,R₃ շառավիղներով երեք շրջանագծերի շոշափման կետերով անցնող շրջանագծի շառավիղը՝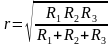 : ^{[ 1; էջ 70 ]}

Ապացույց: Դիցուք A,B,C կետերը շոշափման կետեր են: Հետևաբար O₁O₂O₃եռանկյան համար A, B, C կետերով անցնող շրջանագիծը համարվում է ներգծված:Որպես մի կետից տարված շոշափողների հատվածներ`OA=OB=OC, իսկ OA-ն,OB-ն,OC-ն ուղղահայաց են համապատասխանաբար O₁O₂,O₂O₃,O₃O₁ կողմերին(ըստ շրջանագծի շոշափողի հատկության),հետևաբար O կետը հավասարահեռ է O₁O₂O₃ եռանկյան կողմերից և հանդիսանում է նրան ներգծած շրջանագծի կենտրոն:

A

O₂

O

C

B

O₁

O₃

Գումարելով (1),(2),(3 )հավասարությունները`կստանանք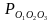 = 2R<sub>1</sub>+2R<sub>2</sub>+2R<sub>3</sub>: Նկատենք, որ P=R<sub>1</sub>+R<sub>2</sub>+R<sub>3</sub> (կիսապարագիծ): Օգտվելով եռանկյան մակերեսի Հերոնի բանաձևից՝կստանանք` = = :

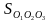Ըստ եռանկյան մակերեսի S=Pr բանաձևի`

r = = =

Այսպիսով`r= :

Խնդիր2. Ապացուցել, որ ուղղանկյուն եռանկյան ուղիղ անկյան գագաթից ներքնաձիգին տարված բարձրությունը եռանկյունը տրոհում է երկու ուղղանկյուն եռանկյունների, որոնց համար տեղի ունեն.

1.P²=P₁ ² +P₂ ² 2. r²= r₁² + r₂² 3. R² = R²₁ + R²₂

(P,P₁,P₂-ը համապատասխանաբար ABC,ACH,BCH եռանկյունների պարագծերն են, r,r₁,r₂-ը՝ ներգծած շրջանագծերի ,R,R₁,R₂-ը՝ արտագծած շրջանագծերի շառավիղները)

4.O₁O₂ = r (Օ₁,Օ₂-ը համապատասխանաբար ACH և BCH եռանկյուններին ներգծած շրջանագծերի կենտրոններն են)

A

B

H

O₁

Օ₃

O₂

C

B

Օ₄

Pr =P₁r₁+P₂r₂ (1) հավասարությաներկուկողմըբաժանենքr-ի,կստանանք՝P=P₁∙ ++P₂ ստ եռանկյուններինմանության` ապաP=P<sub>1</sub> P<sub>2</sub> : Հավասարման երկուկողմը բազմապատկենքP-ով:Կստանանք հետևյալ հավասարությունը`P² = P²₁ + P₂²:Այժմ(1)հավասարության երկու կողմը բաժանենք p-ի՝ կստանանք r= + Ըստ ( 2) և (3) հավասարությունների՝ :Այս հավասարության երկու կողմը բազմապատկենք r-ով, կստանանք՝r² = r₁²+ r₂²։ Իսկ այժմ գտնենք O₁O₂ հեռավորությունը:

Ուղղ. եռանկյուն –ից՝

= =

Այսպիսով :

A

H

O₃

նելով 4-ի՝ կստանանք` R²=R²₁+R²₂ :Քանի որ AB = 2R, իսկ

O₄

C

B

4

Խնդիր 3. Ապացուցել, որ ուղղանկյուն եռանկյանը արտագծած շրջանագիծը եռանկյան գագաթներով տրոհվում է երեք աղեղների, որոնց միջնակետերով անցնող եռանկյան մակերեսը հավասար է տրված ուղղանկյուն եռանկյան կիսապարագծի և շրջանագծի շառավղի արտադրյալի կեսին։^{[ 3 ; էջ 197 ]}

K

A

M

O

C

B

P

եռանկյան մակերեսը:

Այսպիսով՝ որտեղ P-ն ABC եռանկյան կիսապարագիծն է:

S_MKP = :

Խնդիր 4․Ուղղանկյուն եռանկյանը ներգծված է շրջանագիծ և միացված են շոշափ-

ման կետերը։ Ապացուցել, որ առաջացած եռանկյան մակերեսը հավասար է տրված

ուղղանկյուն եռանկյան կիսապարագծի և շրջանագծի շառավղի քառակուսու արտա-

դրյալը հարաբերած ներքնաձիգին։^{[ 4 ; էջ199 ]}

K

A

M

O

C

N

B

Քանի որ S_MKN=S_MON+S_MOK+S_KON,ապա ըստ եռանկյան մակերեսի բանաձևի՝

Այսպիսով՝ որտեղ P-ն ABC եռանկյանկիսապարագիծնէ: S_MKN= :

Գրականություն

1.Երկրաչափություն 7, 8, 9-րդ դաս., Լ. Ս. Աթանասյան, Վ. Ֆ. Բուտուզով ,

Ս.Բ. Կադոմցև, Է. Հ.Պոզնյակ, Ի. Ի. Յուդինա : Երևան 2006

2.Մաթեմատիկայի թեստային առաջադրանքների շտեմարան: Հեղ. խումբ՝ Ս.Ռաֆայելյան,Վ.Փիլիպոսյան,Գ.Միքայելյան,Օ.Միքայելյան,Վ.Ոսկանյան,

Կ. Առաքելյան,Ա. Սարգսյան, Ն. Պողոսյան, Բ. Փիլիպոսյան:

Երևան Րաբունի ՍՊԸ 2015:

3. Մաթեմատիկայի թեստեր ՀՌՀ-ի ընդունելության քննությունների համար:

Երևան ՀՌՀ հրատարակչություն 2015:

ՕԺԱՆԴԱԿ ԽՆԴԻՐՆԵՐ ՀԱՐԹԱՉԱՓՈՒԹՅՈՒՆԻՑ

Սիլվա Ղազարյան

Նյութի հակիրճ ամփոփում

Երկրաչափության դպրոցական դասընթացը ընդգրկում է մեծ քանակությամբ խնդիրներ, որոնք լուծվում են որոշակի ալգորիթմներով։ Օրինակ այն խնդիրները, որոնք ամրապնդում են բանաձևերի իմացությունը և զուտ հաշվողական բնույթի են, չեն կարող ապահովել սովորողների ստեղծագործական մտածողության զարգացումը։ Իսկ ոչ ստանդարտ խնդիրը չի կարող լուծվել նախապես հայտնի ալգորիթմով, անհրաժեշտութուն է առաջանում սկսել լուծման որոնումը, որը և ենթադրում է մտածողության զարգացում։ Աշակերտի մոտ հետաքրքրություն է առաջանում ինքնուրույն փնտրելու և գտնելու խնդրի լուծումը։ Դրա համար աշակերտը պետք է ունենա տեսական գիտելիքների հարուստ պաշար և կարողանա արդեն լուծված խնդիրներում հայտնաբերել կարևոր փաստեր և դրանք ընդհանրացնել։ Երկրաչափական փաստերը, որոնք կարելի է ձևակերպել որպես թեորեմներ,անվերջ են: Դրանցից շատերը հանդես են գալիս երկրաչափության դասագրքերում որպես ապացույցի խնդիրներ: Վերջիններիս իմացությունը և կիրա-ռումը մի շարք խնդիրների լուծում դարձնում է ավելի արդյունավետ և արագ:

ВСПОМОГАТЕЛЬНЫЕ ЗАДАЧИ ПО ПЛАНИМЕТРИИ

С. В. Казарян

Резюме

В статье рассматриваются примеры практического применения дополнительных задач на уроках математики, где основное внимание уделяется умению решать задачи. Большинство из них решается по стандартным схемам, но есть и такие к которым универсальные подходы неприменимы, поэтому дополнительные задачи могут быть использованы при решении некоторых геометрических задач.

ՕԺԱՆԴԱԿ ԽՆԴԻՐՆԵՐ ՀԱՐԹԱՉԱՓՈՒԹՅՈՒՆԻՑ