Относительность механического движения

Относительность механического движения

Подготовила студентка группы КМ 21-20

Прейскурантова Полина

Механическое движение

• Механи́ческим движе́нием называют изменение пространственного положения тела или его частей относительно других тел с течением времени. При этом взаимодействие тел приводит к изменению их скоростей или к их деформации. Механическое движение изучает механика. Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой; причины же движения изучает динамика.

• В более общем значении движением называют изменение состояния физической системы с течением времени. Например, можно говорить о движении волны в среде.

Относительность механического движения

• Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. Для описания движения следует выбрать систему отсчёта, состоящую из системы координат (для указания положения в пространстве) и часов (для указания времени).

Относительность механического движения

Движущиеся тела изменяют своё положение относительно других тел в пространстве с течением времени. Положение автомобиля, мчащегося по шоссе, изменяется относительно указателей на километровых столбах, положение корабля, плывущего в море недалеко от берега, меняется относительно береговой линии, а о движении самолёта, летящего над землей, можно судить по изменению его положения относительно поверхности Земли. Можно показать, что одно и то же тело при одном и том же движении может одновременно по-разному перемещаться относительно разных тел.

Таким образом говорить о том, что какое-то тело движется, можно лишь тогда, когда ясно, относительно какого другого тела — тела отсчета, изменилось его положение.

Два стрелка неподвижны относительно друг друга, но движутся, если рассматривать другие системы отсчёта.

Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.

Галилей показал, что в условиях Земли практически справедлив закон инерции. Согласно этому закону действие на тело сил проявляется в изменениях скорости; для поддержания же движения с неизменной по величине и направлению скоростью не требуется присутствия сил. Системы отсчета, в которых выполняется закон инерции, стали называть инерциальные системы отсчета (ИСО).

Системы, которые вращаются или ускоряются, неинерциальные.

Принцип относительности Галилея

Принцип относительности Галилея гласит: Механические явления протекают одинаково во всех инерциальных системах отсчета, т. е. описывающие их законы динамики одинаковы. Поэтому все инерциальные системы отсчета равноправны. Это значит, что уравнения, выражающие законы механики, не меняются при преобразованиях Галилея.

Г. Галилей и И. Ньютон глубоко осознавали то, что мы сегодня называем принципом относительности, согласно которому механические законы физики должны быть одинаковыми во всех ИСО при одинаковых начальных условиях.

Из этого следует: ни одна ИСО ничем не отличается от другой системы отсчета. Все ИСО эквивалентны с точки зрения механических явлений. Принцип относительности Галилея исходит из некоторых допущений, которые опираются на наш повседневный опыт. В классической механике пространство и время считаются абсолютными. Предполагается, что длина тел одинакова в любой системе отсчета и что время в различных системах отсчета течет одинаково. Предполагается, что масса тела, а также все силы остаются неизменными при переходе из одной ИСО в другую. В справедливости принципа относительности нас убеждает повседневный опыт, например в равномерно движущемся поезде или самолете тела движутся так же, как и на Земле. Не существует эксперимента, с помощью которого можно было бы установить, какая система отсчета действительно покоится, а какая движется. Нет систем отсчета в состоянии абсолютного покоя. Если на движущейся тележке подбросить монету вертикально вверх, то в системе отсчета, связанной с тележкой, будет изменяться только координата ОУ. В системе отсчета, связанной с Землей, изменяются координаты ОУ и ОХ. Следовательно, положение тел и их скорости в разных системах отсчета различны.

Виды механического движения

• Движение материальной точки
• полностью определяется изменением её координат во времени (например, для плоскости — изменением абсциссы и ординаты). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
• Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
• Криволинейное движение — движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).

Виды механического движения

• Движение твёрдого тела
• складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
• Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Движение при этом не обязательно является прямолинейным.
• Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, — используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
• Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела — положением любых двух точек.

Виды механического движения

• Движение сплошной среды
• Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости), поэтому число определяющих координат бесконечно (неизвестными становятся функции).

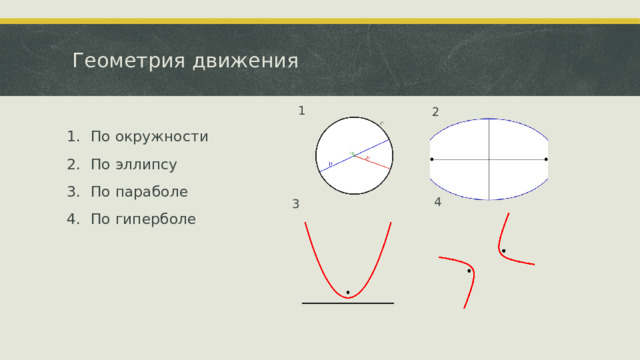
Геометрия движения

1

2

• По окружности
• По эллипсу
• По параболе
• По гиперболе

4

3

Геометрия движения

Равномерное движение

• Квадратриса;
• Кривая погони. Эволюта (огибающая нормалей) трактрисы: (цепная линия, поверхность которой — катеноид);

• Время спуска под действием только силы тяжести не зависит от расположения начальной точки на дуге циклоиды

Геометрия движения

Под действием однородного гравитационного поля

• Кривая скорейшего спуска
• Время спуска под действием только силы тяжести не зависит от расположения начальной точки на дуге циклоиды
• Лемниската Бернулли: материальная точка, движущаяся по кривой под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду. При этом ось лемнискаты составляет угол с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки.

• Движение под действием однородного гравитационного поля

Рассмотрим движение одного и того же тела относительно двух разных систем отсчета: неподвижной и движущейся.

Лодка пересекает реку перпендикулярно течению реки двигаясь с некоторой скоростью относительно воды. За движением лодки следят 2 наблюдателя: один неподвижный на берегу, другой на плоту, плывущем по течению. Относительно воды плот неподвижен, а по отношению к берегу он движется со скоростью течения.

С каждым наблюдателем свяжем систему координат:

X0Y – неподвижная система координат.

X’0’Y’ – подвижная система координат. S – перемещение лодки относительно неподвижной СО.

S1 – перемещение лодки относительно подвижной СО

S2 – перемещение подвижной системы отсчета относительно неподвижной СО.

По закону сложения векторов

Скорость получим разделив S на t:

v – скорость тела относительно неподвижной СО

v1 – скорость тела относительно подвижной СО

v2 – скорость подвижной системы отсчета относительно неподвижной СО

Эта формула выражает классический закон сложения скоростей: скорость тела относительно неподвижной СО равна геометрической сумме скорости тела относительно подвижной СО и скорости подвижной СО относительно неподвижной СО.

В скалярном виде формула будет иметь вид:

Впервые эту формулу получил Галилей.

СПАСИБО ЗА ВНИМАНИЕ!