Тема урока: «Построение графиков функций y=mf(х), y=msinx, y=mcosx
Цели урока:
1) научиться строить графики функций y=msinx, y=mcosx
2 )провести первичный контроль знаний
3) способствовать самостоятельной деятельности учащихся;
4) развивать логическое мышление
Ход урока
I.Организационный момент
II.Устная работа
Вопросы:
1)Как называется график тригонометрической функции y=sinx
2)Назовите свойства этой функции
3) Укажите область значений функций
а) y=cosx б) y=cosx+2 в) y= -5cosx
4)Какая из функций является нечетной?
а) y=cosx+1 б) у=sin2x в) y=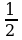 cos2x
cos2x
5) Найдите наибольшее целое значение функций
а) y=-6,5sinx б) y=4,3cosx в) y=-cosx-18
6) Какие свойства функций здесь записаны
а) f(-x)=f(x)
б) f(x)=f(x+T)
в) Если x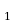 x
x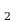 и f(x
и f(x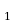 ) f(x
) f(x ) ,то…
) ,то…
III. Новая тема
На столе появляется камертон
Знаком ли вам этот прибор?
Его предназначение в чем?
На какую ноту он настроен?
Каков принцип его работы?
Колебания какой частоты улавливает наше ухо?
А какие ещё характеристики звука вы знаете? (громкость, частота, тембр)
Появляется на столе математический маятник.
Математический маятник совершает колебания. И высота этих колебаний отчего зависит?
(Отклонения от положения равновесия)
Можно ли записать уравнение колебаний? (Да, функция y=sinx описывает колебания)
Если задавать различные отклонения от положения равновесия, то как это отразится на
формуле функции?
Итак, тема урока: Построение графиков функций y=msinx, y=mcosx
Гипотеза.Ваши предположения. Как строить график этой функции?
Презентация №1 Слайды 24-28
Выводы: Как влияет коэффициент перед функцией на график функции?
Слайд 29
IV.Самостоятельная работа проверочного характера.Слайды 30 и 32
Проверка работы. Слайды 31,33
V.Что нового узнали на уроке? Были на уроке какие-то открытия для вас?
VI. Домашнее задание №17.2,17.5,17.7,17.9(а,б)

 Получите свидетельство
Получите свидетельство Вход
Вход












 Открытый урок в 10а классе по теме " Построение графиков тригонометрических функций у=msinx (21.06 KB)
Открытый урок в 10а классе по теме " Построение графиков тригонометрических функций у=msinx (21.06 KB)
 0
0 169
169 2
2 Нравится
0
Нравится
0


