Открытый урок "Центральные и вписанные углы" (8 класс)

Решение геометрических задач для подготовки к ГИА.

Эпиграф к уроку:

  «Вдохновение нужно в геометрии не меньше, чем в поэзии»

(А. С. Пушкин)

Цель урока: Совершенствование умений и навыков решения геометрических задач для подготовки к ГИА.

Задачи:

• Повторить теорию по геометрии по теме «Центральные и вписанные углы».
• Продолжить обучение по применению теории на практике- при решении задач в группах.

Вопросы по теории:

1. Треугольник называется равнобедренным _______  

2 . В равнобедренном треугольнике _______

3. Касательной к окружности называется ______

4. Касательная к окружности перпендикулярна ______

5. Центральным углом называется ______

6. Центральный угол измеряется ______

7. Вписанным углом называется ______

8. Вписанный угол равен ______

Укажите номера верных утверждений?

1. Сумма углов треугольника не превышает 180 0 .

2. Если вписанный угол равен 30 0 , то центральный угол, опирающийся на ту же дугу окружности , равен 60 0 .

3. Вписанные углы , опирающиеся на одну и ту же хорду окружности , равны.

4. Вписанные углы окружности равны.

5. Если дуга окружности составляет 80 0 , то центральный угол, опирающийся на эту дугу , равен 40 0 .

Укажите номера верных утверждений?

1. Сумма углов треугольника не превышает 180 0 .

2. Если вписанный угол равен 30 0 , то центральный угол, опирающийся на ту же дугу окружности , равен 60 0 .

3. Вписанные углы , опирающиеся на одну и ту же хорду окружности , равны.

4. Вписанные углы окружности равны.

5. Если дуга окружности составляет 80 0 , то центральный угол, опирающийся на эту дугу , равен 40 0 .

Ответ : 2,3.

Укажите номера верных утверждений?

1. Вписанные углы, опирающиеся на одну и ту же дугу окружности , равны.

2. Если вписанный угол равен 20 0 ,то дуга окружности , на которую опирается этот угол , равна 40 0 .

3. Внешний угол треугольника равен сумме двух внутренних углов.

4. Центральный угол в два раза больше вписанного угла , опирающегося на ту же дугу.

5. Вписанный угол, опирающийся на полуокружность, меньше 90 0 .

Укажите номера верных утверждений?

1. Вписанные углы, опирающиеся на одну и ту же дугу окружности , равны.

2. Если вписанный угол равен 20 0 ,то дуга окружности , на которую опирается этот угол , равна 40 0 .

3. Внешний угол треугольника равен сумме двух внутренних углов.

4. Центральный угол в два раза больше вписанного угла , опирающегося на ту же дугу.

5. Вписанный угол, опирающийся на полуокружность, меньше 90 0 .

Ответ : 1,2,4.

Решение задач устно

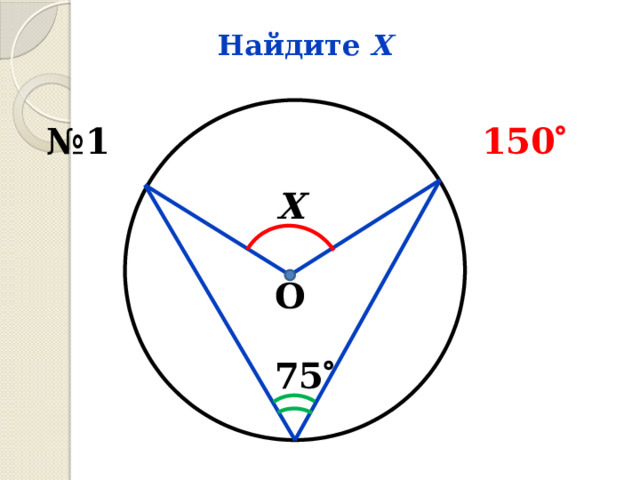
Найдите Х

№ 1

150 

Х

О

75 

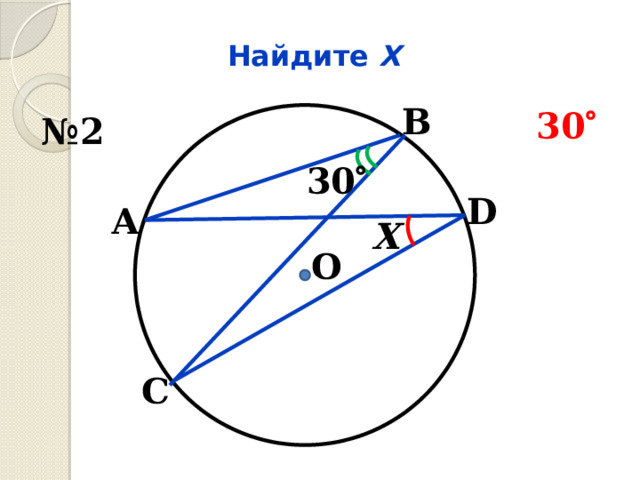
Найдите Х

В

30 

№ 2

30 

D

А

Х

О

С

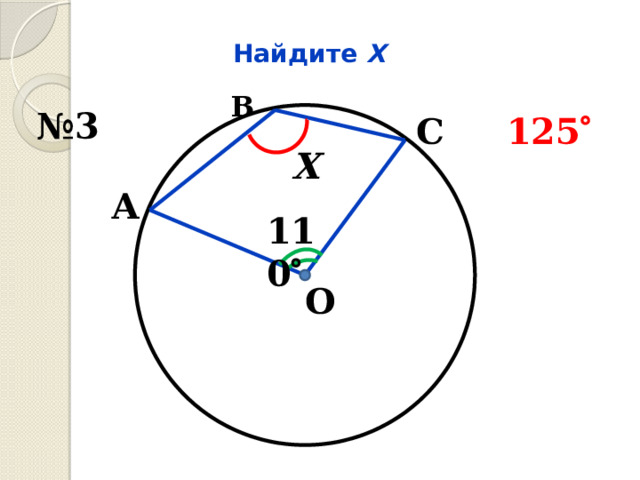
Найдите Х

В

№ 3

С

125 

Х

А

110 

О

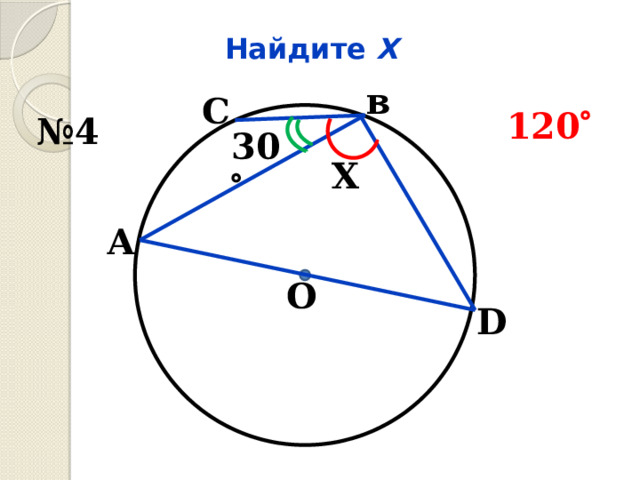
Найдите Х

в

С

120 

№ 4

30 

Х

А

О

D

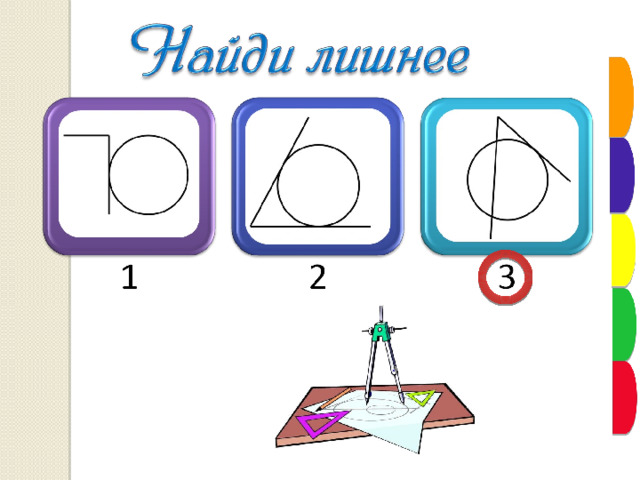
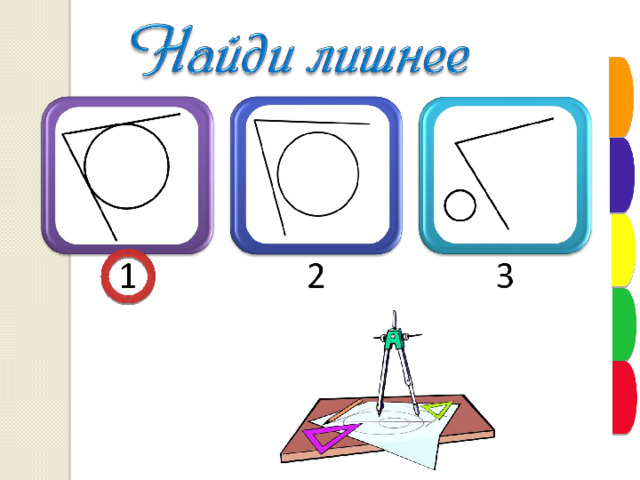
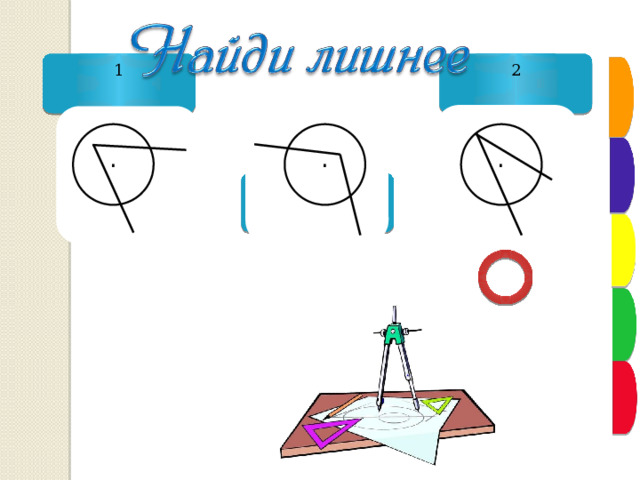
1

2

.

.

.

3

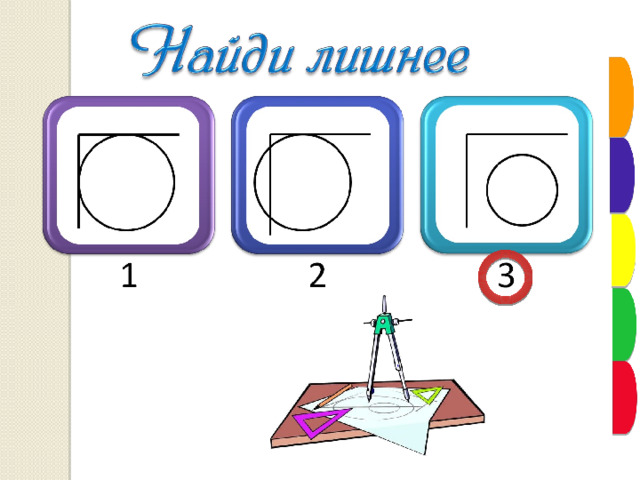
Итог урока

1 – урок полезен, все понятно. 2 – лишь кое-что чуть-чуть неясно. 3 – ещё придется потрудиться. 5 – да, трудно все-таки учиться!

Спасибо

за урок!