Открытый урок по теме: "Изгиб, основные понятия и расчет на прочность"

Тема урока: Изгиб, основные понятия и расчет на прочность.

Цель урока:

Обучающая: Ознакомление с новыми видами деформаций.

Развивающая: Развитие навыков применения приобретенных знаний и умений на практике.

Воспитательная: Воспитание умения анализировать и находить правильные решения встречающихся производственных задач.

Вид урока: комбинированный

Методы обучения применяемые на уроке: вопрос-ответ, объяснение, тест, решение задач.

Наглядные средства обучения: таблицы, чертежи, инструкционные карты, проектор.

Межпредметные связи: математика, физика, материаловедение.

Ход урока:

І.Организационный момент (1 мин)

1) Психологическая подготовка.

2) Подготовка кабинета.

ІІ.Опрос домашнего задания: (8мин)

1. Для контроля уровня освоенности материала прошедшего занятия прошу ответить на вопросы мини-теста из пяти заданий, при этом заполните ячейки для правильных ответов и свои личные данные до конца опроса по прошедшей теме.

2. На дом были заданы 3 задачи по расчету брусьев на кручение. Прошу выйти к доске для изложения своего варианта решения 1-й и 2-й задачи.

3. Вспомним основные понятия сопротивления материалов на которых основан расчет брусьев на прочность.

3.1 вопрос Чем занимается сопротивление материалов?

Ответ: Методами расчета элементов конструкций на прочность, жесткость и устойчивость.

3.2 вопрос Перечислите основные понятия сопротивления материалов.

Ответ: Деформация, прочность, жесткость, брус, виды внешних сил, внутренних сил, метод сечений, напряжения.

4 вопрос. Перечислите виды простых деформаций бруса с показом на плакате.

Ответ: 1.Растяжение и сжатие.2. Сдвиг, 3. Кручение, 4. Изгиб.

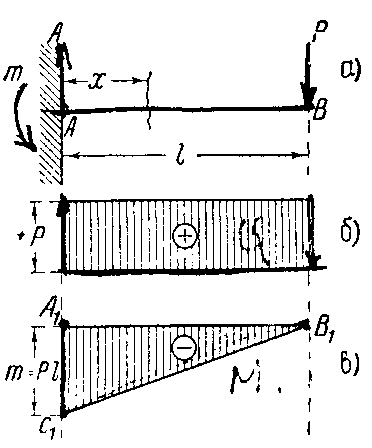
5 вопрос. Что называется кручением? При этом покажите на каком рисунке ниже показан деформация кручения.

Ответ: Кручением называется деформация, возникаяющая при действии на

брус пары сил, расположенный в плоскости, перпендиклярной к его оси. Кручение показан на рисунке а), б).

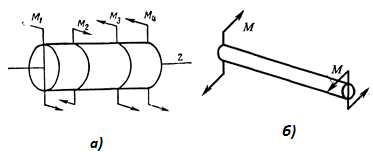
6 вопрос. Какая деталь машин больше всего подвергается деформации кручения ?

Ответ: вал

7 вопрос. Какой внутренний силовой фактор или внутренняя сила возникает во время деформации кручения и как обозначается?

Ответ: Крутящий момент и обозначается М_z или М_к .

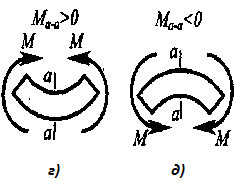
8 вопрос. Что называется эпюрой крутящих моментов и из приведенных рисунков выберите эту эпюру?

Ответ: Эпюрой крутящих моментов называется график, показывающий изменение величины крутящего момента по длине бруса-вала, и изображение этой эпюры следующий рисунок - а).

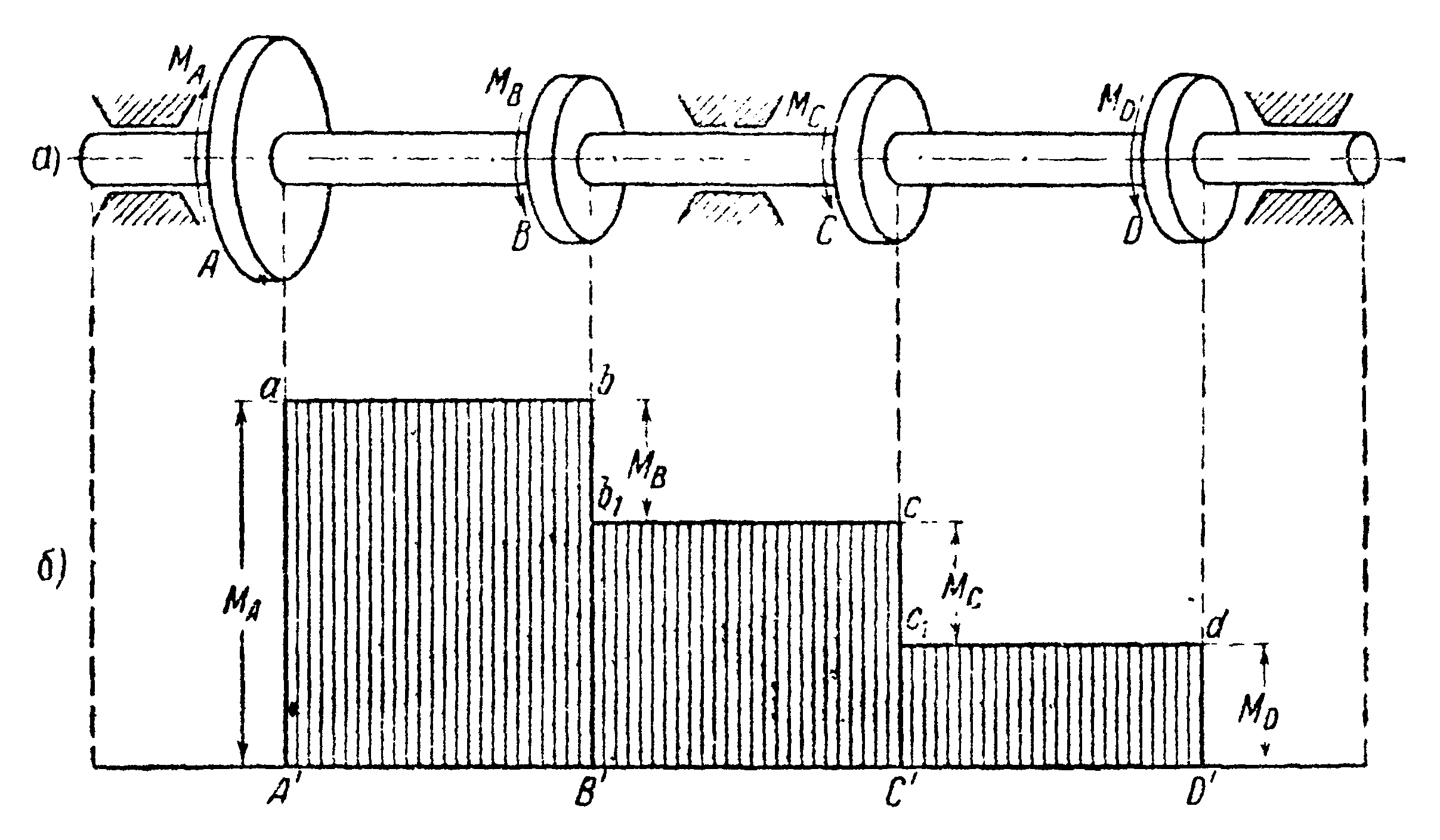
а)

б)

9 вопрос. Каким методом определяют внутреннюю силу – крутящий момент М_к=М_z и приведите формулу для определения касательного напряжения при кручении?

Ответ: а) методом сечений определяют крутящий момент и б) формула напряжения выглядит так

Где τ_max («тау максмум»)– максимальное напряжение при кручении, М_к – максимальный крутящий момент в сечениях бруса, W_p («дубль в пи»)– момент сопротивления кручению,

10 вопрос. Выберите условие прочности при кручении из нижеследущих формул и назовите величины входящие в эту формулу?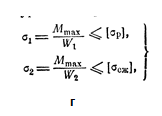

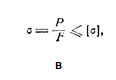
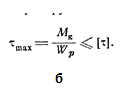
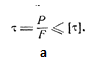
Ответ: формула б), где τ_max («тау максмум») – максимальное напряжение при кручении, М_к – максимальный крутящий момент в сечениях бруса, W_p («дубль в пи») – момент сопротивления кручению, [τ] («тау»)– допускаемое напряжение при кручении.

ІІІ. Объяснение нового материала (30мин).

Тема 1. Изгиб. Классификация видов изгиба. Внутренние силовые факторы при изгибе.Иметь представление о видах изгиба и внутренних силовых факторах.

Знать методы для определения внутренних силовых факторов и уметь ими пользоваться для определения внутренних силовых факторов при прямом изгибе. Основные определенияИзгибом называется такой вид нагружения, при котором в по­перечном сечении бруса возникает внутренний силовой фактор — изгибающий момент.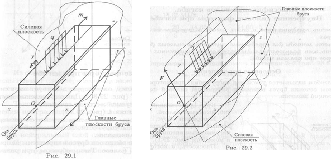

Брус, работающий на из­гиб, называют балкой.

Изображен брус, закреп­ленный справа (защемление), нагруженный внешними силами и моментом (рис. 29.1).

Плоскость, в которой рас­положены внешние силы и моменты, называют силовой плоскостью.Если все силы лежат в од­ной плоскости, изгиб называют плоским.Плоскость, проходящая через продольную ось бруса и одну из главных центральных осей его поперечного сечения, называется главной плоскостью бруса.Если силовая плоскость совпадает с главной плоскостью бруса, изгиб называют прямым (рис. 29.1).Если силовая плоскость не проходит через главную плоскость бруса, изгиб называют косым изгибом (рис. 29.2).

Внутренние силовые факторы при изгибе

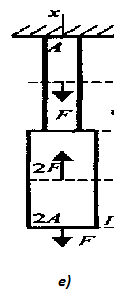
Пример 1. Рассмотрим балку, на которую действует пара сил с моментом т и внешняя сила F (рис. 29.3а). Для определения внут­ренних силовых факторов пользуемся методом сечений.Рассмотрим равновесие участка 1 (рис. 29.36).

Под действием внешней пары сил участок стремится развер­нуться по часовой стрелке. Силы упругости, возникающие в сече­нии 1, удерживают участок в равновесии.

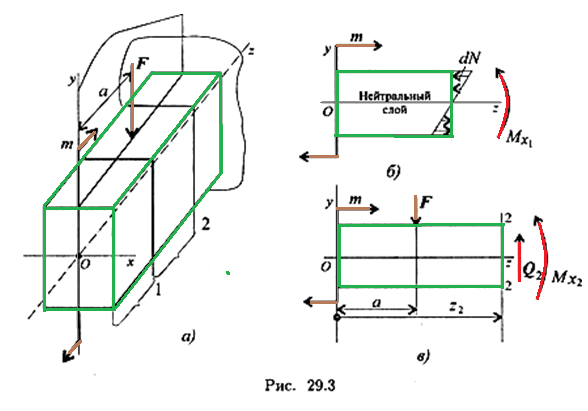Продольные силы упругости выше оси бруса направлены напра­во, а силы ниже оси направлены налево. Таким образом, при равно­весии участка 1 получим: F_z = 0. Продольная сила N в сечении равна нулю. Момент сил упругости относительно оси Ох может быть получен, если суммировать элементарные моменты сил упругости в сечении 1-1 относительно оси Ох:

Из схемы вала на рис. 29.3 б видно, что часть волокон (выше оси) испытывают сжатие, а волокна ниже оси растянуты. Следовательно, в сечении должен существовать слой не растянутый и не сжатый, где напряжения σ равны нулю.

Такой слой называют нейтральным слоем (НС). Линия пересе­чения нейтрального слоя с плоскостью поперечного сечения бруса называют нейтральной осью.Нейтральный слой проходит через центр тяжести сечения. Здесь нейтральный слой совпадает с осью Ох.Практически величина изгибающего момента в сечении опреде­ляется из уравнения равновесия: Σ т_Х1^_₁ = m — М_Х1 = 0; М_Х1 = т.Таким образом, в сечении 1-1 продольная сила равна нулю, из­гибающий момент в сечении постоянен.

Изгиб, при котором в поперечном сечении бруса возникает толь­ко изгибающий момент, называется чистым изгибом.Рассмотрим равновесие участка бруса от свободного конца до сечения 2 (рис. 29.Зв).Запишем уравнения равновесия для участка бруса:

В сечении бруса 2-2 действует поперечная сила, вызывающая сдвиг.

Изгибающий момент в сечении:

z₂ — расстояние от сечения 2 до начала координат.

Изгибающий момент зависит от расстояния сечения до начала координат.

Изгиб, при котором в поперечном сечении бруса возникает изги­бающий момент и поперечная сила, называется поперечным изгибом.

Принятые в машиностроении знаки поперечных сил и изгибающих моментов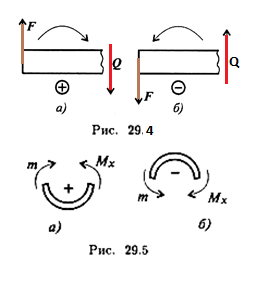

Знаки поперечных сил

Поперечная сила в сече­нии считается положительной, если она стремится развер­нуть сечение по часовой стрелке (рис. 29.4а), если против, — отрицательной (рис. 29.4б).

Знаки изгибающих моментов

Если действующие на участке внешние силы стремятся изогнуть бал­ку выпуклостью вниз, то изгибающий момент считается положительным (рис. 29.5а), если наоборот — отрица­тельным (рис. 29.5б).

Выводы : При чистом изгибе в поперечном сечении балки возникает только изгибающий момент, постоянный по величине.При поперечном изгибе в сечении возникает изгибающий мо­мент и поперечная сила.Изгибающий момент в произвольном сечении балки численно равен алгебраической сумме моментов всех внешних сил, прило­женных к отсеченной части, относительно рассматриваемого се­чения.Поперечная сила в произвольном сечении балки численно равна алгебраической сумме проекций всех внешних сил, действующих на отсеченной части, на соответствующую ось.

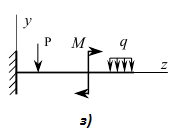
Пример 2. На балку действует пара сил с моментом т и рас­пределенная нагрузка интенсивностью q. Балка защемлена справа

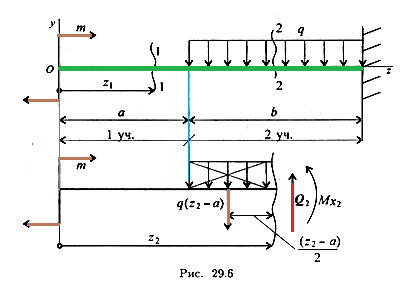
Рассечем балку на участке 1 на расстоянии z₁ от левого края. Рассмотрим равновесие отсеченной части. Из уравнения

получим:

Участок 1 — участок чистого изгиба.

Рассечем балку на участке 2 на расстоянии z₂ а от края, z₂ — расстояние сечения от начала координат.

Из уравнения ΣFy ⁼ 0 найдем поперечную силу Q_2. Заменя­ем распределенную нагрузку на рассматриваемом участке равнодей­ствующей силой q(z₂ — а).

Из уравнения моментов определяем изгибающий момент в сече­нии:

На втором участке возникает поперечный изгиб.

Выводы

При действии распределенной нагрузки возникает поперечная сила, линейно зависящая от координаты сечения.

Изгибающий момент на участке с распределенной нагрузкой меняется в зависимости от координаты сечения по параболическо­му закону.

Дифференциальные зависимости при прямом поперечном изгибе

Построение эпюр поперечных сил и изгибающих моментов су­щественно упрощается при использовании дифференциальных зави­симостей между изгибающим моментом, поперечной силой и интен­сивностью равномерно распределенной нагрузки (теорема Журавского):

Поперечная сила равна производной от изгибающего момента по длине балки:

Интенсивность равномерно распределенной нагрузки равна про­изводной от поперечной силы по длине балки:

Из выше указанного следует:

Тема 2. Изгиб. Построение эпюр поперечных сил и изгибающих моментов. Основные правила построения эпюр.Знать порядок построения и контроля эпюр поперечных сил и изгибающих моментов.Уметь строить эпюры поперечных сил и изгибающих моментов.Эпюры поперечных сил и изгибающих моментов можно строить, предварительно разделив балку на участки нагружения и составляя уравнения, выражающие изменения Q и М_х по участкам.Напомним, что границы участков нагружения — это сечения, в которых приложены внешние нагрузки.Примеры решения задач

Пример 1. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.50, а.

Решение

При построении эпюр для балок с одним защемленным концом можно не определять опорные реак­ции. Проводя сечение, будем рассматривать равновесие той части, к которой приложены только внешние (актив­ные) силы. Для балки по рис. 2.50, а такой частью будет левая.Рассматривая равнове­сие левой отсеченной час­ти балки, выразим попе­речную силу и изгиба­ющий момент в произволь­ном сечении

Поперечная сила положи­тельна, так как внешняя нагрузка направлена сле­ва от сечения вверх, Q_y постоянна на всем протяжении балки. Эпюра поперечных сил построена на рис. 2.50, б.

Оба слагаемых, входящих в выражение изгибающего момента, положительны, так как соответствующие внеш­ние силы изгибают балку выпуклостью вниз. Изгибающий момент выражается линейной функцией от абсциссы се­чения z. Поэтому для построения этой эпюры достаточно найти значения изгибающего момента только в двух се­чениях балки:

Эпюра моментов показана на рис. 2.50, в.

Пример 2. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.52, а.

Решение

Определяем опорные реакции. Реакция V _А направлена вверх, V_B — вниз, так как эти реакции об­разуют пару сил, уравновешивающую пару с моментом т. Составляя суммы моментов относительно опорных точек А и В, находим:

Для проверки опорных реакций составляем сумму проекций на вертикальную ось:

следовательно, реакции вычислены правильно.

Балка имеет два участка I, II. Проводим произволь­ное сечение на участке I на расстоянии z от опоры А и рассматриваем левую отсеченную часть. Поперечная сила на этом участке постоянна, равна реакции V_А и положи­тельна, так как эта реакция направлена вверх и прило­жена слева от сечения.

Изгибающий момент в произвольном сече­нии участка I

Момент положите­лен, так как сила V_A изгибает балку выпук­лостью вниз.

В произвольном се­чении участка II попе­речная сила будет та­кой же, как на участ­ке I:

Изгибающий момент в произвольном сечении участ­ка II

Вычислим изгибающий момент в начале и в конце участка II:

Эпюры Q_y и М_х показаны на рис. 2.52, б, в. В сече­нии, где приложен сосредоточенный момент, в эпюре из­гибающих моментов имеется скачок, равный по величине внешнему моменту.

Тема 2.6. Изгиб. Нормальные напряжения при изгибе. Расчеты на прочность.

Знать распределение нормальных напряжений по сечению бал­ки при чистом изгибе, расчетные формулы и условия прочности.

Уметь выполнять проектировочные и проверочные расчеты на прочность, выбирать рациональные формы поперечных сечений.

Деформации при чистом изгибе

При чистом изгибе в сечении возникает только один внутренний силовой фактор — изгибающий момент.Рассмотрим деформацию бруса, нагруженного внешней парой сил с моментом т (рис. 32.1а)_.При чистом изгибе выполняются гипотезы плоских сечений и ненадавливаемости слоев.

Сечения бруса, плоские и пер­пендикулярные продольной оси, после деформации остаются плоскими и пер­пендикулярными продольной оси.

Продольные волокна не давят друг на друга, поэтому слои испытывают простое растяжение или сжатие.Действуют только нормальные на­пряжения. Поперечные размеры сечений не меняются.Продольная ось бруса после дефор­мации изгиба искривляется и образует дугу окружности радиуса ρ (рис. 32.1б). Материал подчиняется закону Гука.Можно заметить, что слои, расположенные выше продольной оси, растянуты, расположенные ниже оси — сжаты (рис. 32.1б). Так как деформации по высоте сечения меняются непрерывно, имеется слой, в котором нормальные напряжения σ равны нулю; такой слой называют нейтральным слоем (НС). Доказано, нейтральный слой проходит через центр тяжести сечения; ρ — радиус кривизны ней­трального слоя.Рассмотрим деформа­цию слоя, расположенного на расстоянии у от ней­тральной оси (участок АВ, рис. 32.1).

Длина участка до дефор­мации равна длине нейтраль­ной оси:

Абсолютное удлинение слоя

(рис. 32.1б).

Относительное удлинение

Относительное удлинение прямо пропорционально расстоянию слоя до нейтральной оси.

Используем закон Гука при растяжении: σ = Еε.

Получим зависимость нормального напряжения при изгибе от положения слоя:

Формула для расчета нормальных напряжений при изгибе

Рассмотрим изогнутый участок бруса dz (рис. 32.2).

dN — элементарная продоль­ная сила в точке сечения;

dA — площадь элементарной площадки;

dm — элементарный момент, образованный силой относитель­но нейтрального слоя.

Суммарный изгибающий момент сил упругости в сечении

— осевой момент инерции сечения (лекция 25). Таким образом,

Откуда: Ранее получено

После ряда преобразований получим формулу для определения нормальных напряжений в любом слое поперечного сечения бруса:

где J_x — геометрическая характеристика сечения при изгибе.

Эпюра распределения нормальных напряжений при изгибе изоб­ражена на рис. 32.3.По эпюре распределения нор­мальных напряжений видно, что максимальное напряжение возникает на поверхности.

Подставим в формулу напряжения значение у = y_max

Получим

Отношение принято обозначать W_x.

Эта величина называется моментом сопротивления сечения при изгибе, или осевым моментом сопротивления. Размерность — мм³.

W_x характеризует влияние формы и размеров сечения на проч­ность при изгибе. Напряжение на поверхности

Расчет, на прочность при изгибе

Рассчитать на прочность — это значит определить напряжение и сравнить его с допустимым.

Условие прочности при изгибе:

где [σ_иJ — допускаемое напряжение.

По этому неравенству проводят проверочные расчеты после окончания конструирования балки.

Для балок из хрупких материалов расчеты ведут по растянутой и сжатой зоне одновременно (рис. 32.8).

При проектировочном расчете определя­ют потребные размеры поперечных сечений балки или подбирают материал.

Схема нагружения и действующие нагрузки известны.

По условию прочности можно определить нагрузочную способ­ность балки [М_и] = W_x [сг].

ІҮ. Закрепление пройденного материала:

1.Конспектирование лекций.

2. Вопросы учащимся по пройденной теме.

1. вопрос. Какую плоскость называют силовой?

Ответ: Плоскость, в которой рас­положены внешние силы и моменты, называют силовой плоскостью.

2. вопрос Какой изгиб называют прямым? Что такое косой изгиб?

Ответ: Если силовая плоскость совпадает с главной плоскостью бруса, изгиб называют прямым (рис. 29.1).

Если силовая плоскость не проходит через главную плоскость бруса, изгиб называют косым изгибом (рис. 29.2).

3. вопрос Какие силовые факторы возникают в сечении балки при чистом изгибе?

Ответ: Изгиб, при котором в поперечном сечении бруса возникает толь­ко изгибающий момент.

4. вопрос Какие силовые факторы возникают в сечении при поперечном изгибе?

Ответ: При поперечном изгибе в поперечном сечении бруса возникает изги­бающий момент и поперечная сила.

5. вопрос Определите поперечную силу и изгибающий момент в сечении 1-1 (рис. 29.7). Расстояние сечения от свободного конца балки 5 м.

Ответ: Поперечная сила равна Q₁= F₁ = -10кН, изгибающий момент равен М_изг1 = -F₁*z+m=-10*5+15=-35кН.

6. вопрос Определите величины поперечных сил в сечении 1 и в сече­нии 2 (рис. 30.5).

Ответ: Поперечная сила равна Q₁= 0, Q₂=-20кН.

7. вопрос Напишите формулу для расчета изгибающего момента в се­чении 3 (рис. 30.6).

Ответ: Поперечная сила равна Q₁= F₁ = -10кН, изгибающий момент равен М_изг3 = F₁*z₃ –m+ F₂*(z₃ -4,5)кН.

Ү. Комментирование оценок (1мин).

Оценить студентов за активное участие на уроке

ҮІ. Задание на дом:

1. Твердое усвоение пройденного материала по лекции и дополнение и углубление по учебникам

1. Д.В. Чернилевский и др. Техническая механика. Стр.190-206,251-256,

2. М.С Мовнин, А.Б. Израэлит, А.Г. Рубашкин

Основы технической механки.стр.90-110.

3. Олофинская В.П. Техническая механика с вариантами практических заданий Стр.61-66.

Использованная литература:

1. Д.В. Чернилевский., Техническая механика. Москва,1982

2. М.С Мовнин, А.Б. Израэлит, А.Г. Рубашкин, Основы технической механки.1990.

3. Олофинская В.П. Техническая механика с вариантами практических заданий Москва, 2012,

4. М.С Мовнин, А.Б. Израэлит, А.Г. Рубашкин , Руководства к решению задач по технической механике,Москва,1980.