Тема урока «Призма. Правильная призма»
ЦЕЛЬ УРОКА:
Цель: - организовать деятельность учащихся по формированию у них понятия «призма», представление об элементах призмы, видах, призмы,
понятия « правильная призма», представление об элементах правильной призмы.
актуализировать личностный смысл учащихся к изучению данной темы,
- создать условия для развития познавательного интереса учащихся.
ЗАДАЧИ УРОКА:
Образовательные:
Познакомиться с понятием призмы;
Ввести понятия: призмы, прямой призмы, наклонной призмы, правильной призмы
Ввести понятия элементов призмы.
Воспитательные:
формировать научное мировоззрение;
формировать пространственное воображение
способствовать развитию мыслительных процессов: обобщение, систематизация; развитие памяти, аналитического и логического мышления.
расширить кругозор учащихся.
Развивающие:
активизировать познавательную деятельность учащихся;
развивать навыки самостоятельной работы.
Тип урока: Урок усвоения новых знаний. Продолжительность 45 минут.
Оборудование: опорный конспект, модели геометрических фигур, мультимедийный проектор, экран, раздаточный материал.
Программные средства: мультимединая презентация, выполненная в программе Microsoft Office PowerPoint, тест
План урока.
Организационный момент. Формулировка целей урока. Мотивация учебной деятельности. (3 мин.).
Актуализация знаний (7 мин.).
Объяснение нового материала (15 мин.).
Первичная проверка усвоения материала.( 5мин.)
Первичное закрепление. (10 мин.)
Домашнее задание (2 мин.)
Подведение итогов урока. Рефлексия. (3мин.).
ХОД УРОКА.
Организационный момент. Формулировка целей урока.
Учитель:
«Никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия».
Эти слова, сказанные великим французским архитектором Ле Корбюзье в начале 20 века, очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека.(слайд№1)
Мне кажется, что это хороший ответ на вопрос «Зачем надо изучать геометрию? Где могут пригодиться эти знания?». Эти знания помогут нам научиться решать задачи как на уроках, так при подготовке к ЕГЭ, а главное хорошо понимать мир, в котором мы живем.
Цель нашего урока: - познакомиться с одним из видов многогранников, который наиболее часто встречается в окружающем нас мире, разбор основных понятий связанных с ним. Организовать деятельность учащихся по формированию у них понятия «призма», «правильная призма», представление об элементах призмы, видах призмы, используя ранее изученный материал.
2. Актуализация знаний.
Учитель:
Давайте вспомним с какими темами в 10 классе мы уже работали?
- параллельность прямых и плоскостей;
- перпендикулярность прямых и плоскостей;
- вводили понятие многограннника в общем виде и работали с такими как параллелепипед и тетраэдр.
а) Проверка домашнего задания:
У доки по готовому чертежу- разбор задачи № 219 (1 ученик)
б) Фронтальный опрос по повторению.(работает класс)
Вопросы:
1. Какие прямые в пространстве называются перпендикулярными?
2.Как в пространстве могут располагаться перпендикулярные прямые?
3. Что можно сказать о двух прямых перпендикулярных одной плоскости?
4, В каком случае прямая будет перпендикулярна плоскости?
5. Как установить параллельность прямой и плоскости?
6. Сформулировать теорему о трех перпендикулярах.
7. Как установить параллельность двух плоскостей?
Тест на взаимоконтроль ( учащиеся отвечают на вопросы теста, заполняют оценочный лист и меняются с парой для проверки и выставлению оценки по данному критерию). Критерий оценки выносится на доску учителем.
| 1. Две прямые в пространстве называются перпендикулярными, если угол между ними равен а) 1800 б)3600 в) 900 |
| 2. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая а) перпендикулярна к этой прямой б) скрещена с этой прямой в) параллельна к этой плоскости |
| 3. Прямая называется перпендикулярной к плоскости, если она а) скрещена с любой прямой лежащей в этой плоскости б) перпендикулярна к любой прямой лежащей в этой плоскости в) параллельна к любой прямой лежащей в этой плоскости |
| 4. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая а) скрещена с этой плоскостью б) параллельна к этой плоскости в) перпендикулярна к этой плоскости |
| 5. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она а) перпендикулярна к этой плоскости б) пересекается с этой плоскостью в) параллельна к этой плоскости |
| 6. Если две прямые перпендикулярны к плоскости, то они а) перпендикулярны б) параллельны в) пересекающиеся |
| 7. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость а) перпендикулярна и к самой наклонной б) параллельна и к самой наклонной в )пересекает саму наклонную |
| 8 .Углом между прямой и плоскостью, пересекающей эту плоскость и не перпендикулярной к ней, называется угол между а) прямой и плоскостью б) прямой и наклонной на плоскость в) прямой и ее проекцией на плоскость |
| 9. Прямая, проведенная в плоскости через основание наклонной перпендикулярно этой наклонной а) перпендикулярна и к проекции наклонной б) параллельна проекции наклонной в ) пересекает эту наклонную |
| 10. Прямая называется параллельной к плоскости, если она а) скрещена с любой прямой лежащей в этой плоскости б) перпендикулярна к любой прямой лежащей в этой плоскости в) параллельна к любой прямой лежащей в этой плоскости |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| в | а | б | в | а | б | а | в | а | в |
3. Объяснение нового материала.
Учитель. На прошлом уроке мы выяснили, что все многогранники состоят из граней, которые представляют собой пересечение плоскостей. Значит все изученное ранее нам поможет при изучении новой темы.
В книге немецкого биолога Э. Геккеля «Красота форм в природе» можно прочитать такие строки: "Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы".
Многие многогранники изобрел не человек, а создала природа в виде кристаллов (соли, хрустала, льда). Но есть многогранники, которые наиболее часто встречаются в окружающем нас мире---это… ( призма и ее разновидности).
На сегодняшнем уроке мы поговорим именно об этом многогранники.
Итак тема урока « Призма. Правильная призма».
Мы уже знаем, что поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называют многогранником. Призма-один из видов многогранников
Рассмотрим поэтапно, как строится призма
Разберем основные элементы призмы: (работает класс по готовым чертежам
- вершины
-ребра Делятся на ребра основания и боковые.
-грани Основания – равные многоугольники, лежащие в параллельных плоскостях. Боковые –параллелограммы.
-высота Перпендикуляр, проведенный из какой-либо точки одного основания к плоскости другого основания называется высотой призмы.
Диагонали –а)призмы, б)боковой грани, в) основания.
Виды призмы а) прямая, б) наклонная, в) по п-угольнику в основании.
Правильная призма.
Формулы для площади поверхности и объема призмы.
Сечения
4. Проверка первичного усвоения материала
Тест № 2 (самоконтроль) приготовили оценочные листы и отвечаем на вопросы.
ВНИМАНИЕ!!!! каждое предложение начинается со слов «веришь ли ты…», если вы верите, то ставите « +», если нет « - »
Читает учитель:
|
| Веришь ли ты, что
|
|
|
|
| 1 | многогранник, составленный из двух равных многоугольников расположенных в параллельных плоскостях, и п параллелограммов, называется призмой.(+)
|
|
|
|
| 2 | боковые ребра призмы равны и параллельны (+)
|
|
|
|
| 3 | высота призмы всегда равна ее боковому ребру (-) При проверки объяснить почему.
|
|
|
|
| 4 | прямая призма называется правильной, если ее основания правильные многоугольники.(+)
|
|
|
|
| 5 | площадь поверхности призмы равна сумме площадей боковой поверхности и площадей оснований. (+)
|
|
|
|
| 6 | чтобы вычислить площадь боковой поверхности прямой призмы, достаточно знать высоту призмы и периметр ее основанияй. (+) |
|
|
|
7 ребра, выходящие из одной вершины называются измерениями призмы.(+)
8 все грани прямоугольного параллелепипеда-прямоугольники (+)
9 куб является разновидностью прямой четырехугольной призмы (+)
10 боковые грани любой призмы – прямоугольники .(-) При проверки объяснить почему.
ОТВЕТЫ
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| + | + | - | + | + | + | + | + | + | _ |
Еще ученый Эйлер – гений 18 века вывел зависимость между гранями, вершинами, ребрами для призм. Эта зависимость вошла в историю математики как ТЕОРЕМА Эйлера.
Теорема: В любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2.
Понятно, что в зависимости от того какое основание будет иметь призма, будет изменяться количество ее граней , ребер, вершин. Проверим практическим путем верность этого утверждения.
4. Самостоятельная работа с использованием справочного материала.
(Работа с раздаточным материалом стр. 40- по готовым чертежам).
Г + В = Р + 2
|
| Г(грани) | В(вершины) | Р(ребра) |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Г- количество граней, В- количество вершин, Р- количество ребер.
Вывод : Утверждение верно.
Для решения многих геометрических задач связанных с призмой, нужно будет строить сечения. Давайте вспомним, основные виды сечение для данной фигуры, и основные правила построения сечения. Слайд(№ )
Вопрос: Какие основные принципы надо использовать при построении сечений в прямоугольном параллелепипеде? а) соединение точек, лежащих в одной плоскости; б)пересечение параллельных плоскостей по параллельным прямым; в) метод следов.
Самостоятельная работа на построение сечений призмы. ( по готовым чертежам).
Раздаточный материал №3.
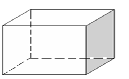
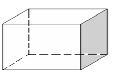

5.Домашнее задание. №221, №229-решить с полным объяснением.
6.Подведение итогов урока. Рефлексия.
Чему научились на уроке? Что удалось? Над чем надо работать?

 Получите свидетельство
Получите свидетельство Вход
Вход















 Открытый урок по геометрии в 10 классе:"Призма. Правильная призма" (44.32 KB)
Открытый урок по геометрии в 10 классе:"Призма. Правильная призма" (44.32 KB)
 0
0 282
282 12
12 Нравится
0
Нравится
0



