Открытый урок по алгебре по теме "Производная" (11 класс)

Тема урока: Производная

ЦЕЛИ УРОКА:

Обучающие: систематизировать знания и умения по теме «Производная»: формулы и правила дифференцирования, геометрический и физический смысл производной, научить применять полученные теоретические знания при решении различного типа математических задач. Подготовка к ЕГЭ. .

Развивающие: развивать творческую и мыслительную деятельность учащихся, способность к «видению проблемы», формировать умение чётко и ясно излагать свои мысли, аргументировать доводы.

Воспитательные: воспитывать умение работать с имеющейся информацией, умение слушать товарищей, оказывать помощь в коллективной деятельности, воспитывать уважение к предмету, воспитывать чувства ответственности и сопереживания

Тип урока: комбинированный: обобщение, закрепление навыков применения свойств элементарных функций, применение уже сформированных знаний, умений и навыков применения производной в нестандартных ситуациях.

Оборудование: компьютер, проектор, экран, раздаточный материал.

«Лишь дифференциальное исчисление дает естествознанию

возможность изображать математически

Не только состояния, но и процессы движения».

Ф.ЭНГЕЛЬС.

ХОД УРОКА

1. Организационный момент

Приветствие.

Обсуждение темы занятия.

-Сегодня на уроке мы поговорим о производной, о её применении.

(вызвать к доске 3 учащихся ,чтоб на доске написать все формулы и правила для вычисления производных . На столе карточки с ответами .выбрать и перевернуть, если правильно решили на доске должны быть слова август 1962 15 январь )

(cu)^/= ( x ⁿ) ^/ ( tgx)^/ =

(u+v)^/= x^/= (ctgx)^/=

(uv)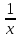^/= ()^/= (lnx)^/=

(u/v)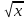^/= ()^/= ( a^x)^/ =

(f(g(x))^/= (sinx)^/= (log_ax)^/=

c^/= (cosx)^/= (e^x)=

-Всем известно высказывание «Мал золотник да дорог». Одним из таких «золотников» в математике является производная. Производная применяется при решении многих практических задач математики, физики, химии, биологии, географии, экономики и других дисциплин. Она позволяет решать задачи просто, красиво, интересно.

- Кто мне скажет –что мы называем производной?

- Зачем нужна производная? Где мы встречаемся с производной и используем её? Можно ли без нее обойтись в математике и не только?

1 ученик. Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д., так как механический смысл производной - это мгновенная скорость.

Производную применяют для исследования функции и построения ее графика, для нахождения наибольшего и наименьшего значений функции.

Слова «производная» и «произошло» имеют похожие части слова, да и смысл похож: производная происходит от исходной функции (переложив на отношения человека: исходная функция - «мама», её производная «дочь»). Производная - часть математической науки, одно из её звеньев. Нет этого звена - прерваны связи между многими понятиями.

2 ученик . Актуальность темы “Производная в школьном курсе математики” следует из того, что человек в повседневной деятельности постоянно сталкивается с решением задач, которые могут быть полностью описаны с помощью функций на математическом языке, а между тем производная является мощным орудием исследования функций. Тема “Производная и ее применения” является одним из основных разделов начал математического анализа. При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Её решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления. Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И. Ньютона и Г.В. Лейбница ). Независимо друг от друга Исаак Ньютон и Готфрид Лейбниц разработали теорию дифференциального исчисления и создали аппарат, которым мы и пользуемся в настоящее время. Исаак Ньютон в основном опирался на физическое представление о мгновенной скорости движения, считая его очевидным и сводя к нему другие случаи производной, а Готфрид Лейбниц использовал понятие бесконечно малой.

3 ученик. Оказывается также, что с помощью производной можно упрощать алгебраические и тригонометрические выражения, раскладывать на множители, доказывать тождества и неравенства и, даже, решать вопрос о существовании корней квадратного уравнения.

На практике часто приходится решать так называемые задачи на оптимизацию (optimum-наилучший) . Инженеры-технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции; конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей; экономисты стараются спланировать связи завода с источниками сырья так , чтобы транспортные расходы оказались минимальными и т.д.

Учитель: Можно сделать вывод, что производная – одно из самых важных понятий математического анализа. Знание производной позволяет решать многочисленные задачи по экономической теории, физике, алгебре и геометрии.

А знаете кто ввел термин «производная»--- Жозеф Луи Лагранж (25.01.1976 – 10.04.1813 )

Французский математик, астроном и механик. 

В 19 лет он стал профессором в Артиллерийской школе Турина. Именно Лагранж в 1791 г. ввёл термин «производная», ему же мы обязаны и современным обозначением производной (с помощью штриха). Термин «вторая производная» и обозначение (два штриха) также ввёл Лагранж.

- а теперь посмотрим ,что получилось на доске

Проверить ,что получилось на доске -август 1962 15 январь

- В начале шестидесятых годов в Каспийске было всего три школы. Они значились в порядке номеров- первая, вторая, третья..

Но город рос, росло и его население. В школах уже не хватало ученических мест. И вот в августе 1962 года состоялось торжественное открытие школы №7

ЗАДАНИЕ 1

- Найти производные и сопоставить с верным ответом .на доске написать какая буква рядом (решить на доске 5,6,9,11)

11) f(x) = ln (5-x)

12) f(x) = 78 π x

13) f(x) = e^2x

14) f(x) = (4х-2)³

ОТВЕТЫ

А) f'(x) = 12x³ – 21x² + 4x Й
Б) f(x) = – 8(3 – 4x)  А
В) f'(x) = – 8x С
Г) f'(x) = 2 А
Д) f'(x) = 2(3x² – 2) (x³ – 2x) Т
Е) f'(x) = sin (3x + р/4) Д
Ж) f'(x) = 5/ sin²(2 – 5x) Ы
З) f'(x) = 6x² – 9cos 3x К
И) f(x) = 2 cosx А
К) f'(x) = 3x² Ш

Л) f'(x) = 12(4х-2)² А

М) f'(x) = 2 e^2x Н

Н) f'(x) =78 π В

О) f'(x) = -1/ (5-x) О

- если верно решили должно получиться -Айшат Садыковна

Это 1 –й директор школы 7 ( до этого она была руководителем школы №2)Айшат Садыковна Мусанабиева.

- а кто мне скажет

1. В чем состоит геометрический смысл производной функции

2. В чем состоит физический смысл производной функции.

3. Какая функция называется дифференцируемой в

точке?

4. Касательная наклонена под тупым углом к положительному направлению оси ОХ.

Следовательно

5. Касательная наклонена под острым углом к положительному направлению оси ОХ. Следовательно,

6. Касательная параллельна оси ОХ, либо с ней совпадает. Следовательно, …

Задания 2 (по рядам) (решить выбрать карточку с ответом ) (один с каждого ряда решает пример на доске , остальные на местах ,потом сравнивают)

1. Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 14х - х² + 5 в точке с абсциссой х₀ = 3. ( 8-АБАСОВ)

2. Найдите тангенс угла наклона касательной к графику функции f(x) = 2х²+ 12х -3 в точке с абсциссой х₀ = 2.(20- АЛИ)

3. При движении тела по прямой расстояние S (в метраx) от начальной точки изменяется по закону S(t) = 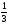t³ - 4t² + 15t + 2 (t - время движения в секундах). Найти скорость (м/с) тела через 2 секунды после начала движения.(3-АБАСОВИЧ.)

-- Вторым директором школы №7 был Али Абасович Абасов который оставил в городе, да, и пожалуй, и в республике, большой и добрый след.

Став директором каспийской школы №7, Али Абасович не только сохранил, но и приумножил ее лучшие традиции. Под его руководством школа стала и лучшим методическим центром для Северного Кавказа по повышению квалификации учителей.

А. Абасов загорелся идеей создать на основе школы гимназию. И его замыслы осуществились …- а это ,если вы знаете- хорошо, но если не знаете ,вы узнаете, выполнив след задания .

Задание 3

1 ряд

На доске написать число, которое получится при делении на (-2) т е 1

ответ 3. На доске умножив на 3= 9)

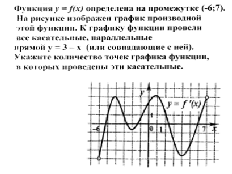
3На рисунке изображён график функции у = f(x) и девять точек на оси абсцисс: . В скольких из этих точек производная функции f(х) отрицательна?

( ответ 3. На доске умножив на 3= 9)

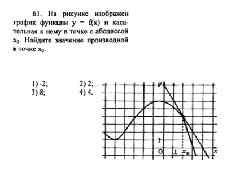
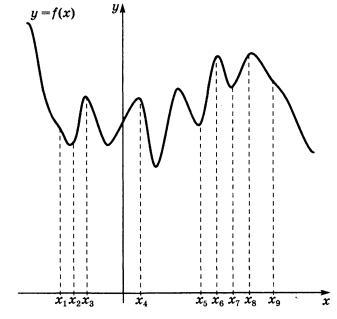
4.На рисунке изображены график функции у=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .( ответ-3

ответ .(1,5 на доске написать прибавив -1,5) т.е. 0

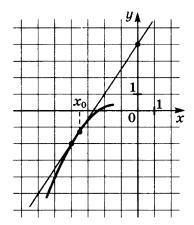
5. Чему равна производная в точке x₀

На доске должно быть 1990 год

-В этом году на основе школы №7 была создана гимназия ,значит, 15 января гимназии исполнится 29 лет, а школе № 7 -57 лет

Физминутка

1.Наклон головы вперёд-назад.

2.Наклон головы влево- вправо.

3.Описать головой полукруг.

4.Руки вперёд, кисти «замком», повороты сцепленными руками влево- вправо.

5.Руки вниз, поднимаем и опускаем плечи

-А теперь след задание (1 -1 ряду,2 -2 ряду,3 -3 ряду). Решить ,найти карточку с ответом и перевернуть

Задание 4

1.Найти наименьшее значение функции у=(х²+25)/х на отрезке [-10;-1]

Ответ: у=-26

2. Определите точку минимума функции

У=(2х²-16х+16)е^28-х

Ответ: х= 2

3. y = (3·x² + 2·x - 4)/x². Найти точку максимума функции

Ответ: х= 4

ответы; -26- ЛЕВИЦКАЯ Л.П.

2- АЛИЕВ М.Х.

4 - МАГОМЕДОВ М.С.

В 2001 году после безвременной кончины А.А. Абасова коллектив гимназии единодушно рекомендовал на должность директора своего завуча Людмилу Петровну Левицкую, которая продолжила прекрасное дело своего предшественника. На посту директора гимназии Людмила Петровна проработала до 2008 года, когда была назначена начальником Управления Образования г.Каспийска.

С 2008 по 2015 г. директором Каспийской гимназии былАлиев Магомед Хузайпович, заслуженный учитель Республики Дагестан, Отличник народного образования Республики Дагестан, Почетный работник общего образования Российской Федерации.

С 21 декабря 2015 г. директором Каспийской гимназии назначен Магомедов Магомед Сайпулаевич.

- Пока все решают задания, один ученик готовится к след заданию

Найти промежутки возрастания и убывания функции 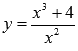.и построить график функции

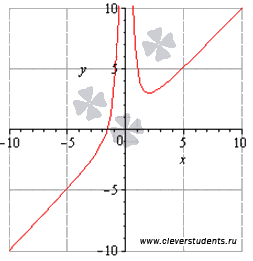
Ответ: функция возрастает при , убывает на интервале (0;2].

Возрастает при х ∈ (-∞; 0)- гимназия

[2; +∞) лучшая

и убывает при х ∈ (0; 2]. –школа

Итог урока (рефлексия результативности, настроения)

-Подведение итогов занятия

-Объявление оценок

-Задание на дом

-Рефлексия

- Каким вопросам был посвящен урок?

- Чему научились на уроке? 

- Какие теоретические факты обобщались на уроке?

Сегодня на уроке получили следующие оценки: (называю учащихся и оценки).