Логика (от греч. LOGOS – слово, понятие, рассуждение, разум) – наука о законах и формах рационального мышления, методах формализации
Основы логики были заложены величайшим древнегреческим философом Аристотелем
внук врачевателя Эскулапа, родился в городе Стагира, занимался воспитанием Александра Македонского.
Родился в Лейпциге в семье профессора философии. Указал пути для перевода логики “из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются совершенно точно”. Лейбниц надеялся даже, что в будущем философы, вместо того чтобы бесплодно спорить, станут брать бумагу и вычислять, кто из них прав. При этом в своих работах Лейбниц затрагивал и двоичную систему счисления. Однако алгебра логики им так и не была создана. Умер одиноким и всеми покинутым.
- Родился в городе Мадура (Индия) шотландский математик и логик. Профессор математики Университетского колледжа в Лондоне. Основные результаты сформулированы в сочинении «Формальная логика...», где он изложил элементы логики высказываний и логики классов, дал первую развитую систему алгебры отношений.
Английский математик-самоучка. Родился в Линкольне (Англия). Сын сапожного мастера. Окончил только начальную школу. С 1849 года – профессор математики. Женился на дочери профессора греческого языка Мери Эверест, она стала матерью четырех дочерей Буля, одна из которых, Этель Лилиан Буль, в замужестве Войнич, - автор популярного романа "Овод". Считается несомненным создателем символической (математической) логики. Его именем назван раздел математической логики - булева алгебра.
Британский логик и философ; основные труды в области логики классов; наиболее известен созданным им особым графическим аппаратом (диаграммы Венна), который используется во многих областях: теория множеств, теория вероятности, логика, статистика, компьютерные науки.
Алгебраические операции
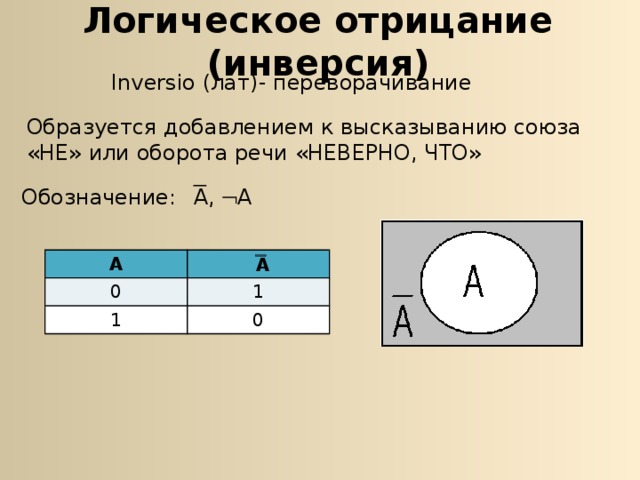
Логическое отрицание (инверсия)
Inversio (лат) - переворачивание
Образуется добавлением к высказыванию союза «НЕ» или оборота речи «НЕВЕРНО, ЧТО»
Обозначение: А, А
А
0
А
1
1
0
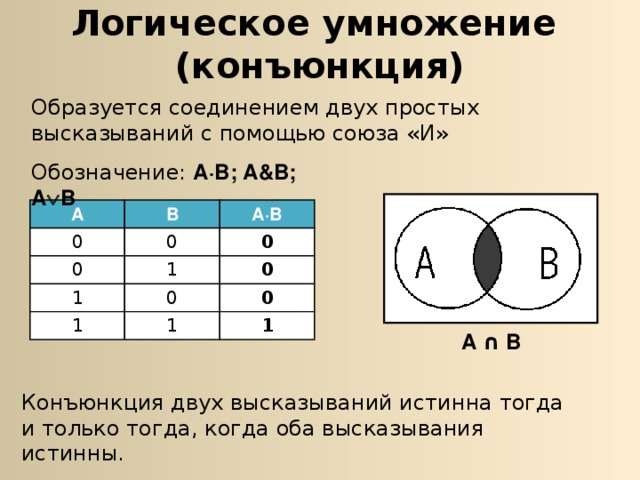
Логическое умножение (конъюнкция)
Образуется соединением двух простых высказываний с помощью союза «И»
Обозначение: А∙В; А&В; А В
А
В
0
А∙В
0
0
1
0
1
0
0
1
1
0
1
А ∩ В
Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны.
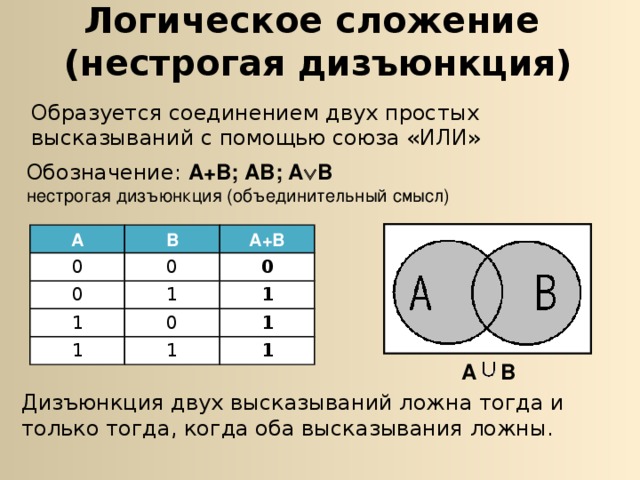
Логическое сложение (нестрогая дизъюнкция)
Образуется соединением двух простых высказываний с помощью союза «ИЛИ»
Обозначение: А+В; АВ; А В нестрогая дизъюнкция (объединительный смысл)
А
0
В
А+В
0
0
0
1
1
1
1
0
1
1
1
А В
Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны.
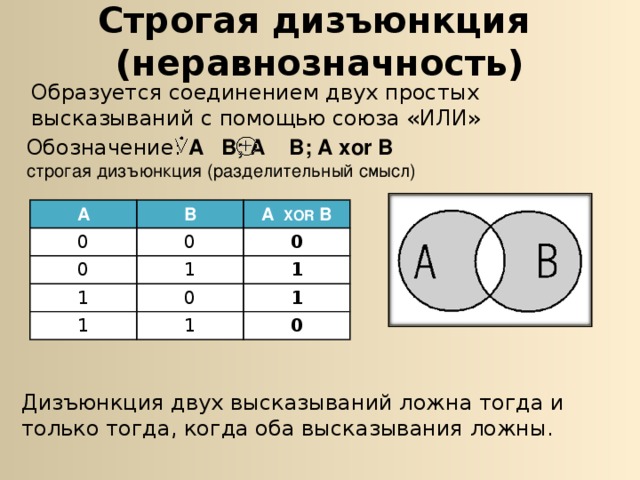
Строгая дизъюнкция (неравнозначность)
Образуется соединением двух простых высказываний с помощью союза «ИЛИ»
Обозначение: А В; А В; А xor В строгая дизъюнкция (разделительный смысл)
А
В
0
0
0
А XOR В
1
1
0
1
0
1
1
1
0
Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны.
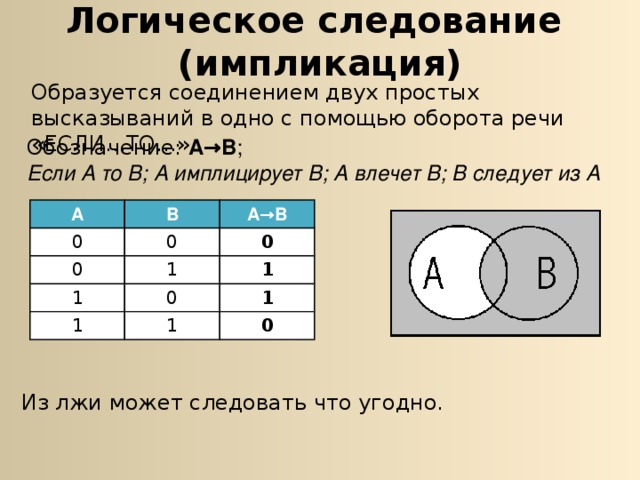
Логическое следование (импликация)
Образуется соединением двух простых высказываний в одно с помощью оборота речи «ЕСЛИ…ТО…»
Обозначение: А→В ; Если А то В; А имплицирует В; А влечет В; В следует из А
А
В
0
0
А→В
0
1
0
1
1
0
1
1
1
0
Из лжи может следовать что угодно.
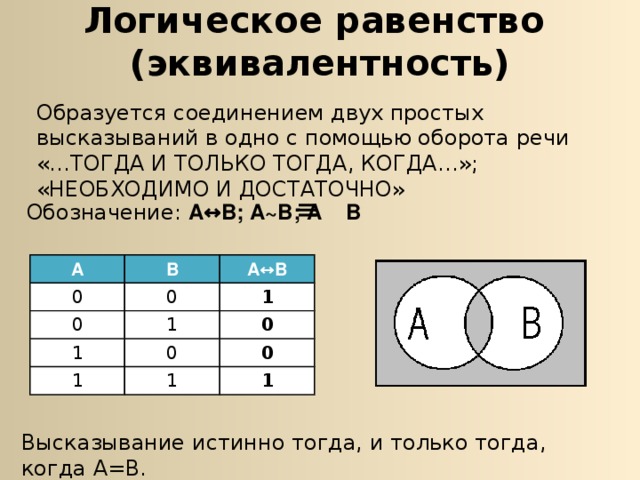
Логическое равенство (эквивалентность)
Образуется соединением двух простых высказываний в одно с помощью оборота речи «…ТОГДА И ТОЛЬКО ТОГДА, КОГДА…»; «НЕОБХОДИМО И ДОСТАТОЧНО»
Обозначение: А↔В; А~В; А В
А
0
В
А↔В
0
0
1
1
1
1
0
0
0
1
1
Высказывание истинно тогда, и только тогда, когда А=В.
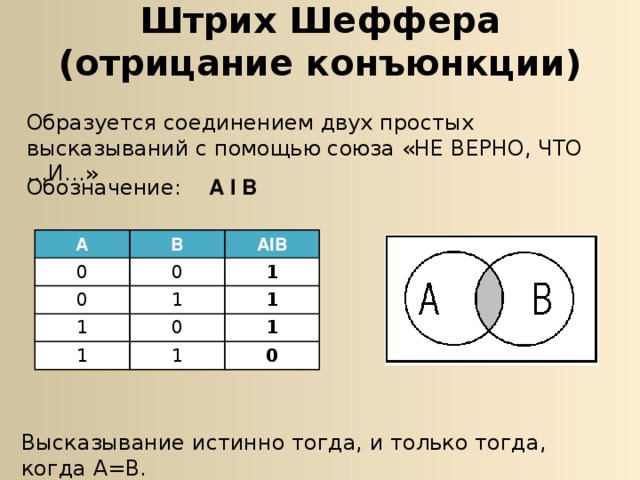
Штрих Шеффера (отрицание конъюнкции)
Образуется соединением двух простых высказываний с помощью союза «НЕ ВЕРНО, ЧТО …И…»
Обозначение: А l В
А
0
В
А l В
0
0
1
1
1
1
1
0
1
1
0
Высказывание истинно тогда, и только тогда, когда А=В.
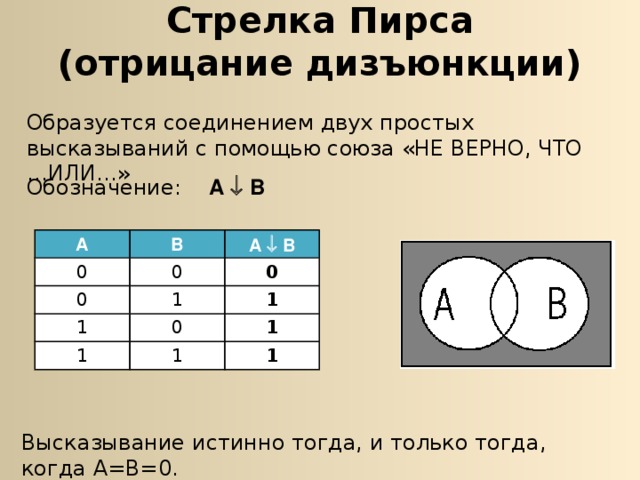
Стрелка Пирса (отрицание дизъюнкции)
Образуется соединением двух простых высказываний с помощью союза «НЕ ВЕРНО, ЧТО …ИЛИ…»
Обозначение: А В
А
0
В
А В
0
0
1
0
1
1
1
0
1
1
1
Высказывание истинно тогда, и только тогда, когда А=В=0.
Алгоритм построения таблиц истинности (ТИ)
- Определить количество строк и столбцов в ТИ
- Начертить таблицу и заполнить заголовок
- Заполнить исходные высказывания
- Заполнить остальные столбцы.
Получите свидетельство
Вход
Основы математической логики (1.22 MB)
0
1115
17
Нравится
0
