10 класс
Найдите сумму корней всех квадратных трехчленов вида
 ,где p принимает все целые значения от -100 до 100.
,где p принимает все целые значения от -100 до 100.
Дана функция от четырех переменных 𝑓(𝑎,𝑏,𝑐,𝑑)=𝑥, которая называется - сложное отношение четырех чисел: a,b,c и d. Найдите чему равно сложное отношение четырех чисел f(d,a,b,c); f(b,d,a,c); f(c,a,b,d); f(b,a,c,d); f(c,b,d,a), если x=5.
Найти площадь выпуклого четырехугольника ABCD, у которого AC=2, BD=1, а отрезки, соединяющие середины противоположных сторон, равны.
Решите систему уравнений:
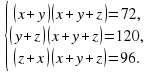
Докажите, что если
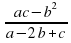 =
= 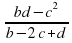 , то обе эти дроби равны выражению:
, то обе эти дроби равны выражению: 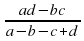 .
.
Решения
Поскольку
 для любого p ,то все трехчлены имеют два корня. Заметим, что по теореме Виета, сумма всех корней трехчлена
для любого p ,то все трехчлены имеют два корня. Заметим, что по теореме Виета, сумма всех корней трехчлена  равна –p , т.е. сумма корней всех написанных трехчленов равна (-100)+(-99)+(-98)+…+98+99+100=0.
равна –p , т.е. сумма корней всех написанных трехчленов равна (-100)+(-99)+(-98)+…+98+99+100=0.
Зная, что сложное отношение выражается формулой
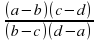 , можно подставить свои числа, например, a=0, b=1, c=2, d=3, подсчитать и получить следующие значения: −
, можно подставить свои числа, например, a=0, b=1, c=2, d=3, подсчитать и получить следующие значения: − 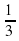 ;
;  ;
; ; 4;
; 4;  ; −3. Заметим, что -3 получается путем обращения числа −
; −3. Заметим, что -3 получается путем обращения числа − 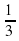 , значит 𝑓(𝑑,𝑎,𝑏,𝑐) =
, значит 𝑓(𝑑,𝑎,𝑏,𝑐) = 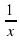 . Число
. Число  получается путем вычитания из 1 числа −
получается путем вычитания из 1 числа − 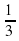 , значит 𝑓(𝑏,𝑑,𝑎,𝑐)= 1− 𝑥. Число 4 получается путем вычитания из 1 числа -3, значит 𝑓(𝑐,𝑎,𝑏,𝑑) =1−
, значит 𝑓(𝑏,𝑑,𝑎,𝑐)= 1− 𝑥. Число 4 получается путем вычитания из 1 числа -3, значит 𝑓(𝑐,𝑎,𝑏,𝑑) =1−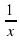 =
=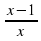 . Число
. Число  получается путем обращения числа 4, значит 𝑓(𝑏,𝑎,𝑐,𝑑)=
получается путем обращения числа 4, значит 𝑓(𝑏,𝑎,𝑐,𝑑)=  . Число
. Число  получается путем обращения числа
получается путем обращения числа  , значит 𝑓(𝑐,𝑏,𝑑,𝑎)=
, значит 𝑓(𝑐,𝑏,𝑑,𝑎)=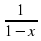 . Теперь, когда каждое число выражено через х и не зависит от а, b, с и d, мы можем вычислить их, подставив вместо х значение 5. 𝑓(𝑑,𝑎,𝑏,𝑐) =
. Теперь, когда каждое число выражено через х и не зависит от а, b, с и d, мы можем вычислить их, подставив вместо х значение 5. 𝑓(𝑑,𝑎,𝑏,𝑐) = 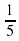 ; 𝑓(𝑏,𝑑,𝑎,𝑐) = −4; 𝑓(𝑐,𝑎,𝑏,𝑑) =
; 𝑓(𝑏,𝑑,𝑎,𝑐) = −4; 𝑓(𝑐,𝑎,𝑏,𝑑) = ; 𝑓(𝑏,𝑎,𝑐,𝑑) =
; 𝑓(𝑏,𝑎,𝑐,𝑑) = ; 𝑓(𝑐,𝑏,𝑑,𝑎) = −
 .
.
EF – средняя линия треугольника ABC , значит EF
AC. HG- средняя линия треугольника ADC, значит HG
AC, но тогда EF
HG. Аналогично доказываем, что EH
FG. Следовательно, EFGH- параллелограмм. Но по условию EG=HF, значит, EFGH – прямоугольник, то есть HG
FG, а тогда BD
AC. Получилось, что диагонали четырехугольника ABCD взаимно перпендикулярны, следовательно, .
Сложив все три уравнения системы, получим уравнение , из которого найдем . Подставляя вместо (x + y + z) числа 12 и - 12,получим в первом случае: x = 2,y = 4, z = 6,а во втором случае x = - 2, y = - 4, z = - 6.
Ответ: (2;4;6), (-2;-4;-6).
Обозначим дроби числами
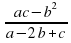 (1),
(1), 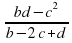 (2) и
(2) и 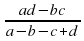 (3). Заметим, что в числителе первой дроби стоит выражение, напоминающее нам условие того, что три числа a, b и c составляют геометрическую прогрессию 𝑎𝑐 − 𝑏2 = 0. Подобное же выражение стоит в числителе второй дроби. В знаменателе мы видим выражение, которое у нас ассоциируется с арифметической прогрессией 𝑎−2𝑏+𝑐=0, условие того, что три числа a, b и c составляют арифметическую прогрессию. В третьей же дроби мы видим своеобразное правило, по которому знаменатели можно вывести из числителей. Например, в числителе произведение ad, а в знаменателе сумма 𝑎+𝑑 в числителе -bc, а в знаменателе -(b+c). Таким же образом получаются числители и знаменатели первой и второй дробей. Зная этот факт, предполагаем, что все три дроби равны, тогда запишем, что все три дроби равны некоторому k. Получаем наши уравнения в следующем виде:
(3). Заметим, что в числителе первой дроби стоит выражение, напоминающее нам условие того, что три числа a, b и c составляют геометрическую прогрессию 𝑎𝑐 − 𝑏2 = 0. Подобное же выражение стоит в числителе второй дроби. В знаменателе мы видим выражение, которое у нас ассоциируется с арифметической прогрессией 𝑎−2𝑏+𝑐=0, условие того, что три числа a, b и c составляют арифметическую прогрессию. В третьей же дроби мы видим своеобразное правило, по которому знаменатели можно вывести из числителей. Например, в числителе произведение ad, а в знаменателе сумма 𝑎+𝑑 в числителе -bc, а в знаменателе -(b+c). Таким же образом получаются числители и знаменатели первой и второй дробей. Зная этот факт, предполагаем, что все три дроби равны, тогда запишем, что все три дроби равны некоторому k. Получаем наши уравнения в следующем виде: ;
;
. Преобразуем первое из получившихся равенств:
⟹ 𝑎𝑐−𝑏2 = 𝑘𝑎−2𝑏𝑘+𝑘𝑐 ⟹ 𝑎𝑐−𝑘𝑎−𝑘𝑐 = 𝑏2−2𝑏𝑘+𝑘2⟹𝑎𝑐−𝑘𝑎−𝑘𝑐+𝑘2=𝑏2−2𝑏𝑘+𝑘2⟹(𝑎−𝑘)(𝑐−𝑘)=(𝑏−𝑘)2⟹ уравнение выражает тот факт, что a-k, b-k и c-k являются членами геометрической прогрессии. Рассматривая аналогичное второе равенство, получаем, что b-k, c-k и d-k тоже члены геометрической прогрессии. Так как по условию (1) = (2), то a-k, b-k, c-k, d-k - составляют геометрическую прогрессию. Но произведение первого и четвертого члена геометрической прогрессии равно произведению второго и третьего членов геометрической прогрессии, т.е.: (𝑎−𝑘)(𝑑−𝑘) = (𝑏−𝑘)(𝑐−𝑘) ⟹ 𝑎𝑑−𝑘𝑑−𝑎𝑘+𝑘2 =𝑏𝑐−𝑏𝑘−𝑐𝑘+𝑘2 ⟹𝑎𝑑−𝑏𝑐=𝑎𝑘−𝑏𝑘−𝑐𝑘+𝑑𝑘 ⟹ 𝑎𝑑−𝑏𝑐𝑎−𝑏−𝑐+𝑑 = 𝑘 т.е.:
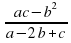 =
= 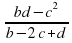 =
= 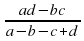

 Получите свидетельство
Получите свидетельство Вход
Вход












 Олимпиадные задания по математике 10 класс. (41.4 KB)
Олимпиадные задания по математике 10 класс. (41.4 KB)
 0
0 6471
6471 236
236 Нравится
0
Нравится
0


