Олимпиадные задания по математике (8 класс)

Задача 1

Два совершенно одинаковых катера, имеющих одинаковую скорость в стоячей воде, проходят по двум различным рекам одинаковое расстояние (по течению) и возвращаются обратно (против течения). В какой реке на эту поездку потребуется больше времени: в реке с быстрым течением или в реке с медленным течением?

Решение

Пусть скорость катеров v км/ч, скорость течения в первой реке v1 км/ч, а скорость течения во второй реке v2 км/ч. Пусть v1>v2. Если обозначить расстояние, проходимое в одном направлении катерами, через S, то время, затраченное первым катером на весь путь, t1 = S/(v+v1) + S/(v-v1) = 2Sv/(v2-v12), а время, затраченное вторым катером, t2 = 2Sv/(v2-v22).

Поскольку числители у обоих выражений одинаковы, то большей будет дробь с меньшим знаменателем, а так как знаменатели есть разности с равными уменьшаемыми, то знаменатель меньше у первой дроби, у которой вычитаемое v12 больше.

Ответ

Больше времени потребуется на поездку в реке с более быстрым течением.

Задача 2

Найти скорость и длину поезда, если известно, что он проходит мимо неподвижного наблюдателя в течение 7 с и затратил 25 с, чтобы проехать вдоль платформы длиной в 378 м.

Полную информацию смотрите в файле. 

Олимпиадные задания по математике 8 класс с решением.

Задача 1

Два совершенно одинаковых катера,
имеющих одинаковую скорость в стоячей воде,
проходят по двум различным рекам одинаковое расстояние
(по течению) и возвращаются обратно (против течения).
В какой реке на эту поездку потребуется больше времени:
в реке с быстрым течением или
в реке с медленным течением?

Решение

Пусть скорость катеров v км/ч,
скорость течения в первой реке v₁ км/ч,
а скорость течения во второй реке v₂ км/ч.
Пусть v₁v₂ .
Если обозначить расстояние, проходимое в одном направлении катерами, через S ,
то время, затраченное первым катером на весь путь,

t₁ = S/(v+v₁) + S/(v-v₁) = 2Sv/(v²-v₁²),

а время, затраченное вторым катером,

t₂ = 2Sv/(v²-v₂²).

Поскольку числители у обоих выражений одинаковы,
то большей будет дробь с меньшим знаменателем,
а так как знаменатели есть разности с равными уменьшаемыми,
то знаменатель меньше у первой дроби,
у которой вычитаемое v₁² больше.

Ответ

Больше времени потребуется на поездку в реке с более быстрым течением.

Задача 2

Найти скорость и длину поезда,

если известно,
что он проходит мимо неподвижного наблюдателя в течение 7 с

и затратил 25 с,
чтобы проехать вдоль платформы длиной в 378 м.

Решение

Пусть x (м) - длина поезда,

y (м/с) - его скорость.

Тогда x/y = 7 и (x + 378)/y = 25 ,

откуда x = 147 (м), y = 21 (м/с).

Скорость можно определить сразу:
для проезда мимо платформы поезду потребовалось 25 - 7 = 18 (с).
Следовательно, его скорость
378 : 18 = 21 (м/с),
длина его 21 х 7 = 147 (м).

Ответ

21 м/с, 147 м.

Задача № 3

Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки меда, 4 тарелки сгущенки и 2 тарелки варенья, а после этого не смог выйти наружу из-за того, что сильно растолстел от такой еды.
Но известно, что если бы он съел 2 тарелки меда, 3 тарелки сгущенки и 4 тарелки варенья или 4 тарелки меда, 2 тарелки сгущенки и 3 тарелки варенья, то спокойно смог бы покинуть нору гостеприимного Кролика.
От чего больше толстеют: от варенья или от сгущенки?

Решение :

По условию 3м + 4с + 2в  2м + 3с + 4в,
откуда м + с  2в. (*)
По условию же 3м + 4с + 2в  4м + 2с + 3в,
откуда 2с  м + в.
Складывая последнее неравенство с неравенством (*), получаем м + 3с  м + 3в, откуда с  в.

Задача № 4

В каждой клетке клетчатой доски размером 50  х  50 записано по числу.
Известно, что каждое число в 3 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по стороне, и в 2 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по диагонали.
Докажите, что каждую клетку доски можно покрасить в красный или синий цвет так, что сумма всех чисел, записанных в красных клетках, равна сумме всех чисел, записанных в синих клетках.

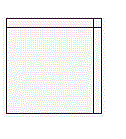
Решение :

Покажем, что подойдет раскраска клеток доски в шахматном порядке. Заметим, что сумма данного числа и его соседей по диагоналям равна сумме соседей этого числа по сторонам: обе суммы втрое больше данного числа. Поэтому в квадрате 2 х 2, находящемся в углу доски, суммы чисел в красных и синих клетках совпадают: обе они втрое больше числа, стоящего в угловой клетке доски. Также совпадают суммы чисел в красных и синих клетках любого прямоугольника 3 х 2, примыкающего длинной стороной к краю доски: обе они втрое больше числа, стоящего в средней клетке стороны, примыкающей к краю доски. Наконец, совпадают суммы чисел в красных и синих клетках любого квадрата 3 х 3: обе они втрое больше числа, стоящего в центре квадрата.

Разобьем доску 50 х 50 на квадрат 48 х 48, квадрат 2 х 2 и два прямоугольника 2 х 48, как показано на рисунке. Квадрат 48 х 48 разобьем на квадраты 3 х 3, а прямоугольники 2 х 48 — на прямоугольники 3 х 2, примыкающие длинной стороной к краю доски. В каждом из этих квадратов и прямоугольников суммы чисел, стоящих в красных и синих клетках, равны. Значит, они равны и на всей доске.