ОГЭ Задание 17. Окружность. Вписанные и центральные углы.

Подготовка к ОГЭ

Задание 17

Окружность Вписанные и центральные углы

(по материалам открытого банка заданий ОГЭ по математике)

Повторение теории

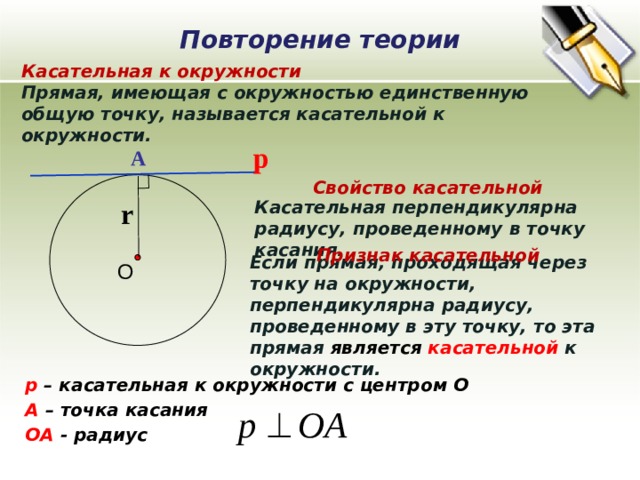
Касательная к окружности

Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.

р

А

Свойство касательной

Касательная перпендикулярна радиусу, проведенному в точку касания.

r

Признак касательной

Если прямая, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то эта прямая  является касательной к окружности.

О

р – касательная к окружности с центром О

А – точка касания

OА - радиус

Повторение теории

В

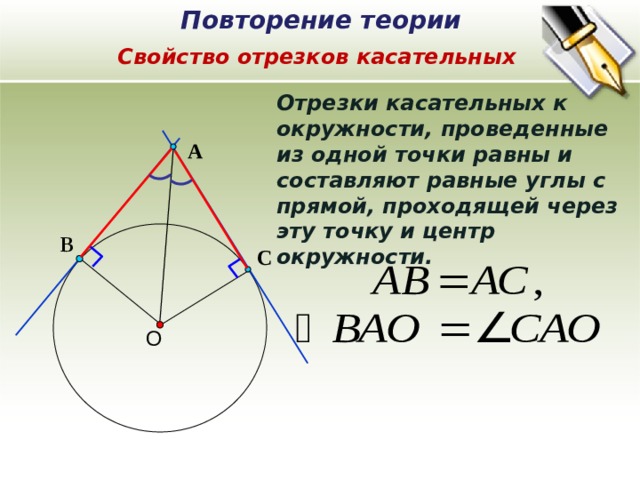
Свойство отрезков касательных

Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

А

С

О

3

Повторение теории

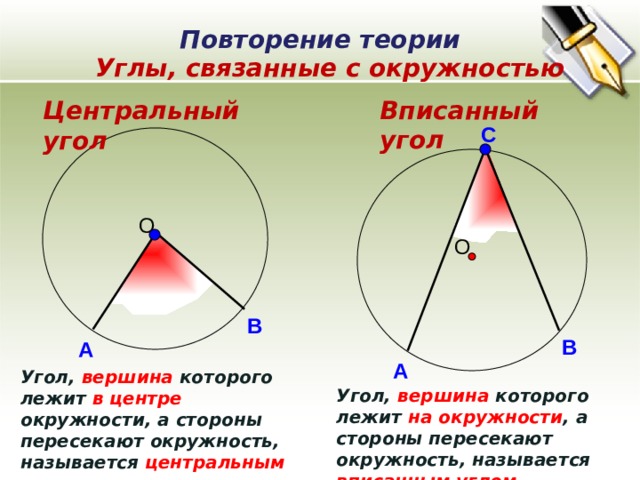
Углы, связанные с окружностью

Вписанный угол

Центральный угол

С

О

О

В

В

А

А

Угол, вершина которого лежит в центре окружности, а стороны пересекают окружность, называется центральным углом .

Угол, вершина которого лежит на окружности , а стороны пересекают окружность, называется вписанным углом .

4

Повторение теории

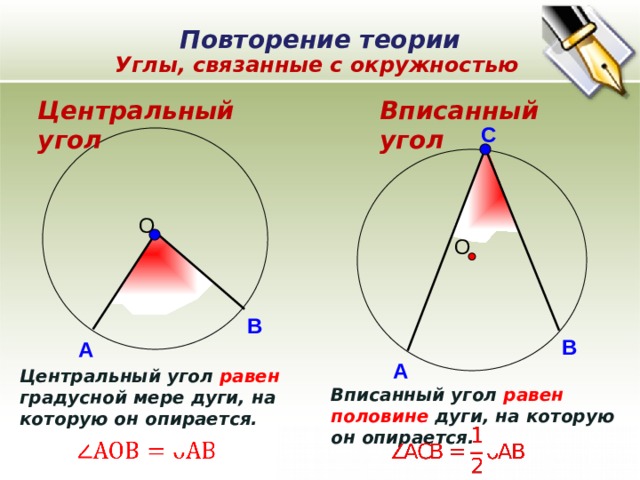
Углы, связанные с окружностью

Вписанный угол

Центральный угол

С

О

О

В

В

А

А

Центральный угол равен градусной мере дуги, на которую он опирается.

Вписанный угол равен половине дуги, на которую он опирается.

5

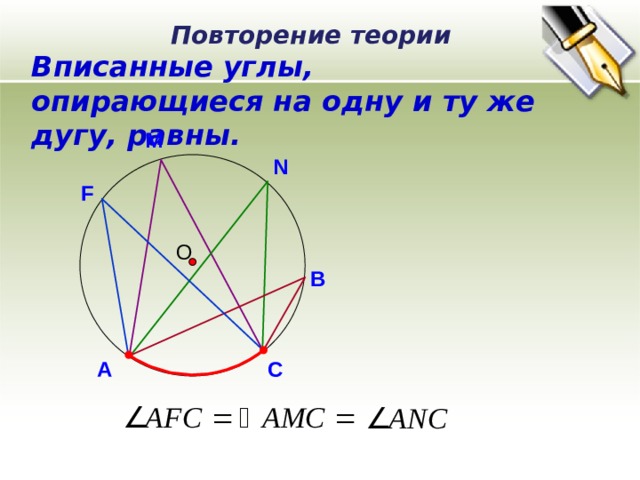
Повторение теории

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

M

N

F

О

В

А

С

6

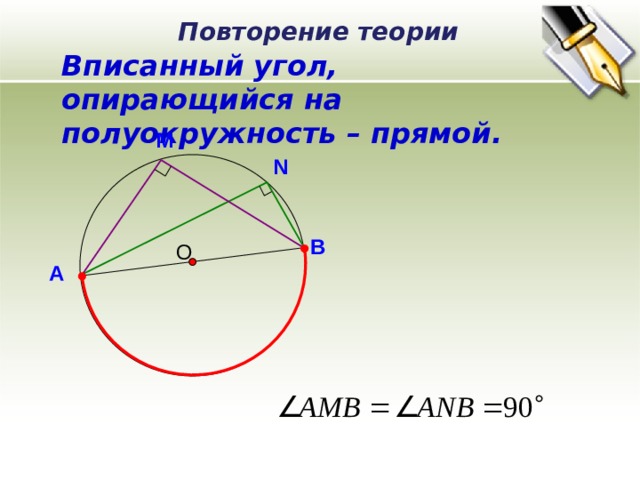
Повторение теории

Вписанный угол, опирающийся на полуокружность – прямой.

M

N

В

О

А

°

7

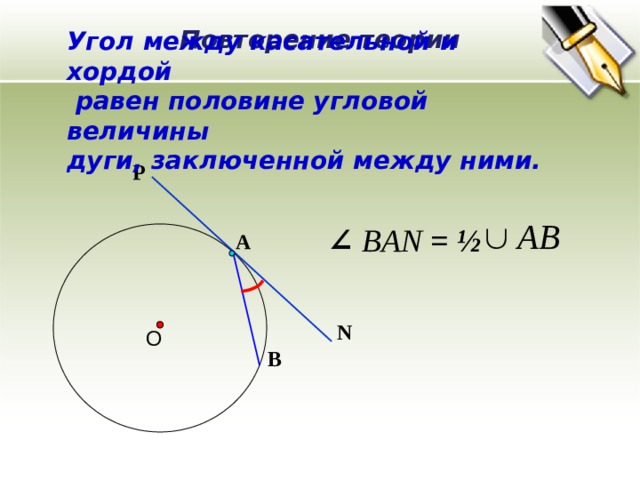
Повторение теории

Угол между касательной и хордой

равен половине угловой величины

дуги, заключенной между ними.

Р

∠ BAN = ½

А

N

О

В

8

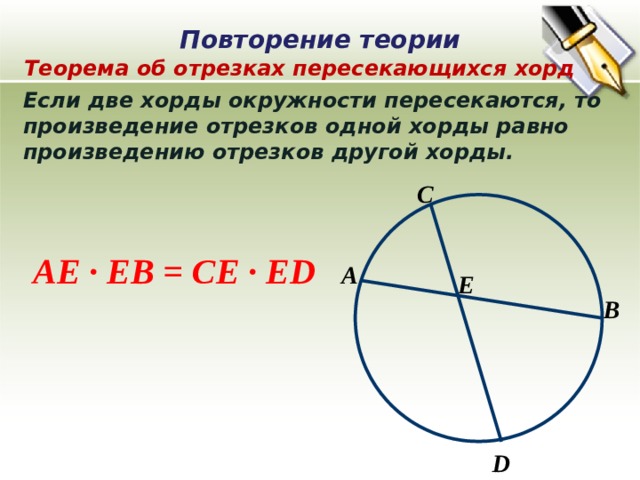
Повторение теории

Теорема об отрезках пересекающихся хорд

Если две хорды окружности пересекаются, то

произведение отрезков одной хорды равно

произведению отрезков другой хорды.

C

АЕ ∙ ЕВ = СЕ ∙ ЕD

А

E

B

D

Повторение теории

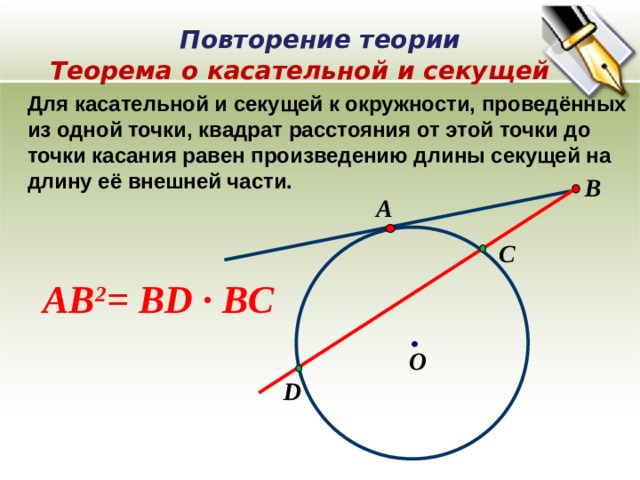
Теорема о касательной и секущей

Для касательной и секущей к окружности, проведённых из одной точки, квадрат расстояния от этой точки до точки касания равен произведению длины секущей на длину её внешней части.

B

А

C

AB 2 = BD ∙ ВC

О

D

Повторение теории

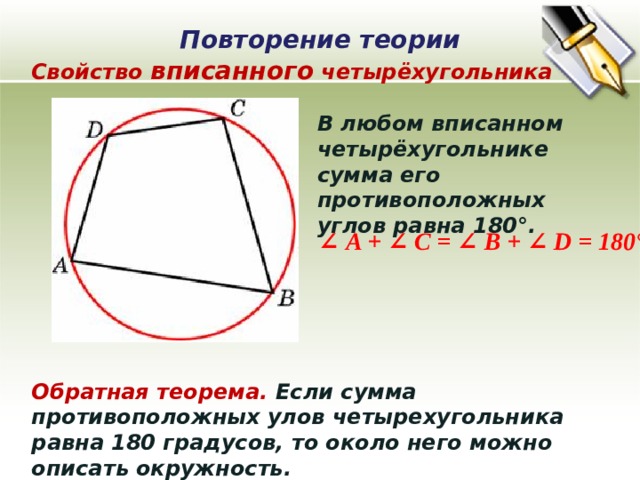
Свойство вписанного четырёхугольника

В любом вписанном четырёхугольнике сумма его противоположных углов равна 180°.

∠ A + ∠ C = ∠ B + ∠ D = 180°

Обратная теорема. Если сумма противоположных улов четырехугольника равна 180 градусов, то около него можно описать окружность.

Повторение теории

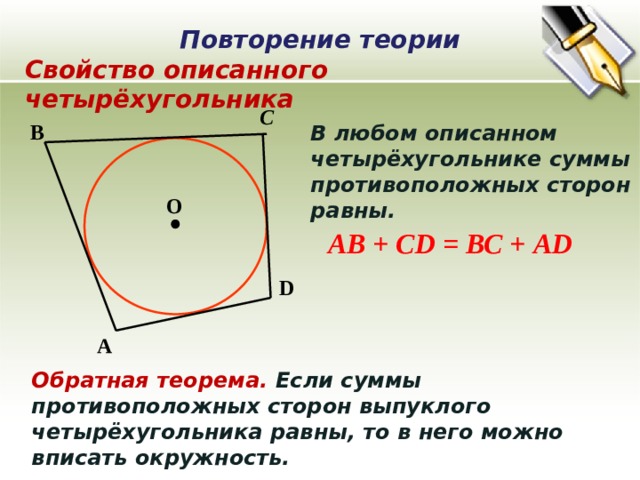
Свойство описанного четырёхугольника

С

В

В любом описанном четырёхугольнике суммы противоположных сторон равны.

О

АВ + СD = ВС + АD

D

А

Обратная теорема. Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.

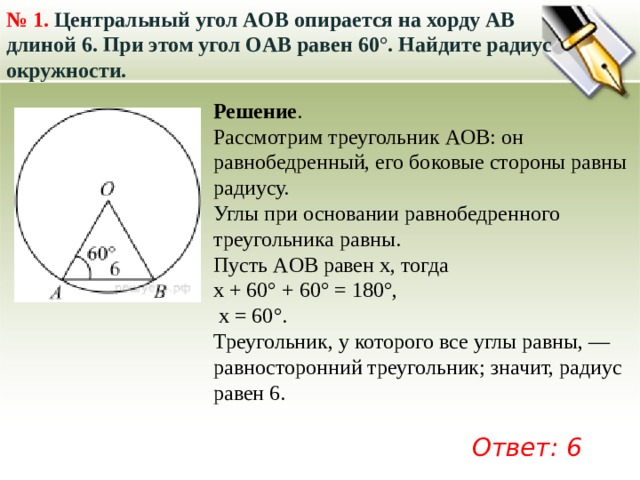
№ 1. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.

Решение .

Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу.

Углы при основании равнобедренного треугольника равны.

Пусть AOB равен x, тогда

x + 60° + 60° = 180°,

x = 60°.

Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.

Ответ: 6

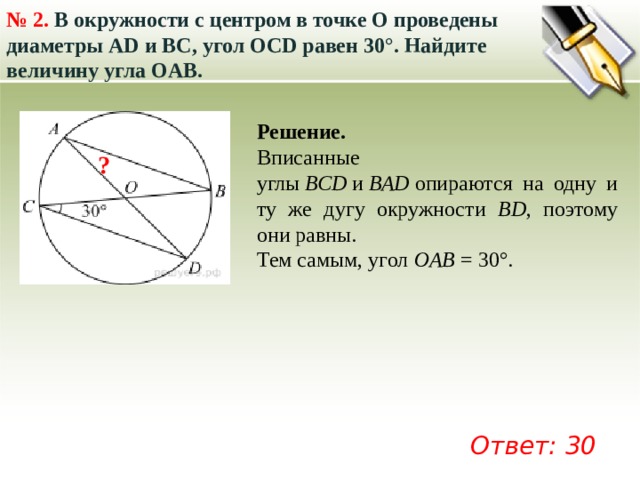
№ 2. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.

Решение.

Вписанные углы  ВСD  и  ВАD  опираются на одну и ту же дугу окружности BD , поэтому они равны.

Тем самым, угол  OAB  = 30°. 

?

Ответ: 30

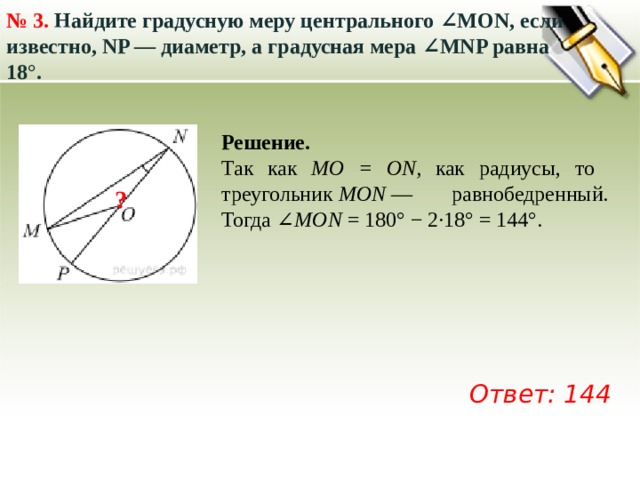
№ 3. Найдите градусную меру центрального ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.

Решение.

Так как MO = ON, как радиусы, то треугольник  MON  — равнобедренный. Тогда ∠ MON  = 180° − 2·18° = 144°.

?

Ответ: 144

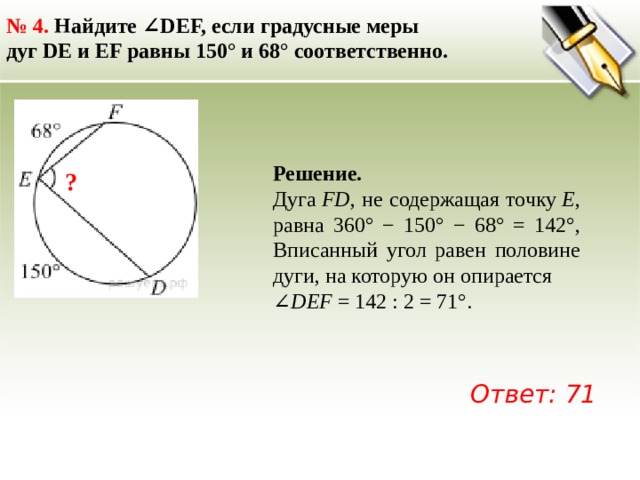
№ 4. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

Решение.

Дуга  FD , не содержащая точку  Е , равна 360° − 150° − 68° = 142°, Вписанный угол равен половине дуги, на которую он опирается

∠ DEF  = 142 : 2 = 71°.

?

Ответ: 71

№ 5. Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера центрального ∠AOC равна 96°.

Решение.

Так как ∠ AOC  и ∠ AOB  — смежные,

∠ AOB  = 84°.

Центральный угол равен дуге на которую он опирается, поэтому градусная мера дуги  AB  равна 84°.

Угол  ACB  — вписанный и равен половине дуги, на которую опирается, поэтому ∠ ACB  = 84° : 2 = 42°.

?

Ответ: 42

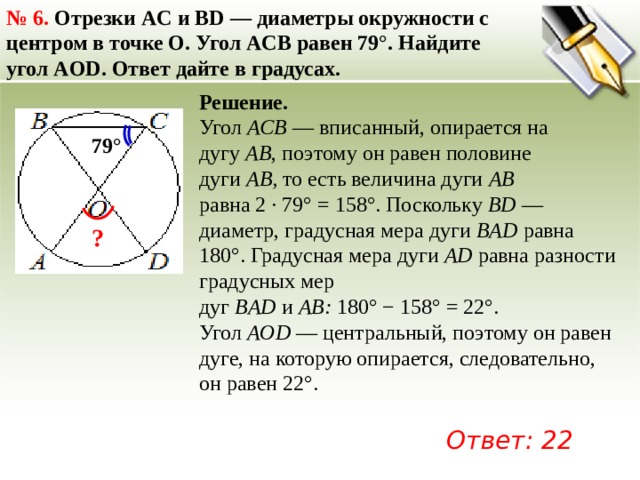
№  6. Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.

Решение.

Угол  ACB  — вписанный, опирается на дугу  AB , поэтому он равен половине дуги  AB,  то есть величина дуги  AB   равна 2 · 79° = 158°. Поскольку  BD  — диаметр, градусная мера дуги  BAD  равна 180°. Градусная мера дуги  AD  равна разности градусных мер дуг  BAD  и  AB:  180° − 158° = 22°. Угол  AOD  — центральный, поэтому он равен дуге, на которую опирается, следовательно, он равен 22°.

79°

?

Ответ: 22

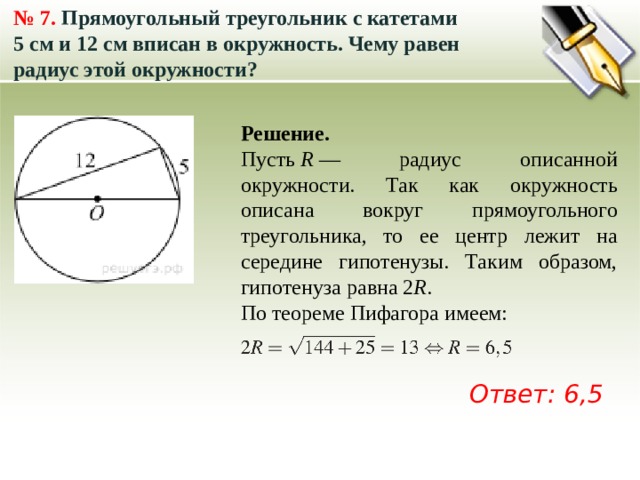
№ 7. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?

Решение.

Пусть  R  — радиус описанной окружности. Так как окружность описана вокруг прямоугольного треугольника, то ее центр лежит на середине гипотенузы. Таким образом, гипотенуза равна 2 R .

По теореме Пифагора имеем:

Ответ: 6,5

№ 8. Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.

Решение.

Дуги окружности относятся как 9:11, что в сумме дает 20 частей.

Поэтому длина меньшей дуги составляет от всей окружности, тем самым, она равна

Так как угол AOB — центральный, то он равен той дуге на которую он опирается. Таким образом, .

Ответ: 162

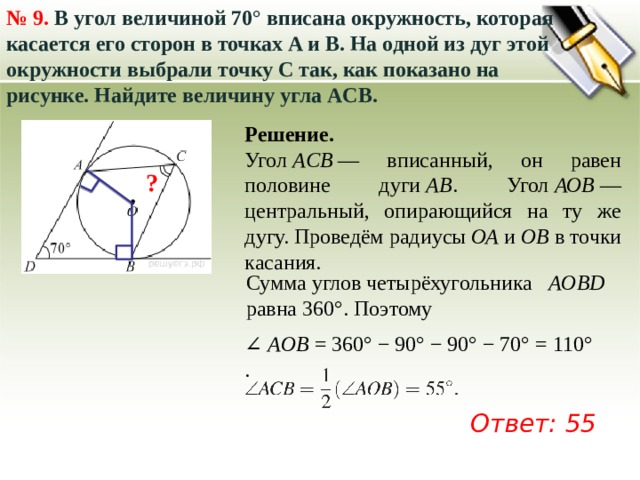
№ 9. В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.

Решение.

Угол  ACB  — вписанный, он равен половине дуги  AB . Угол  АОВ  — центральный, опирающийся на ту же дугу. Проведём радиусы  ОА  и  ОВ  в точки касания.

?

Сумма углов четырёхугольника  AOBD  

равна 360°. Поэтому

∠  AОB  = 360° − 90° − 90° − 70° = 110°.

Ответ: 55

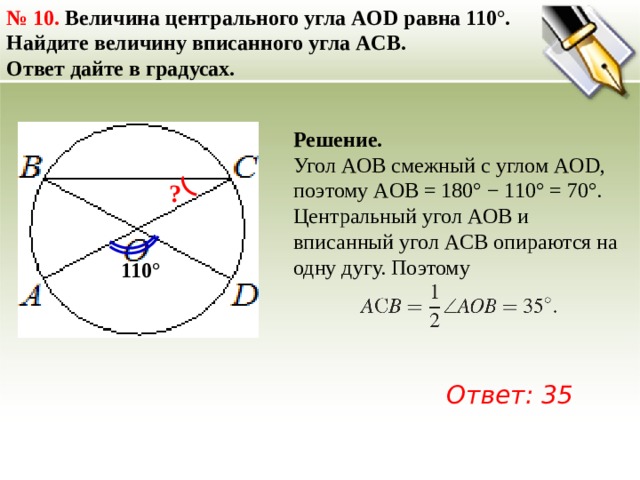
№  10. Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB.

Ответ дайте в градусах.

Решение.

Угол AOB смежный с углом AOD, поэтому AOB = 180° − 110° = 70°. Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Поэтому

?

110°

Ответ: 35

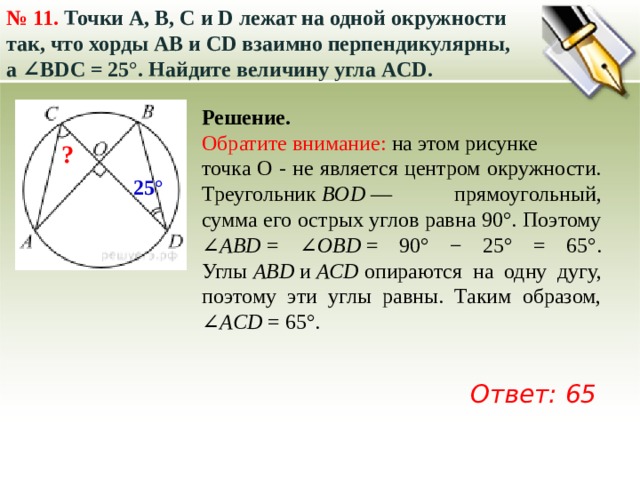
№ 11. Точки A, B, C и D лежат на одной окружности так, что хорды AB и СD взаимно перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.

Решение.

Обратите внимание: на этом рисунке

точка О - не является центром окружности. Треугольник  BOD  — прямоугольный, сумма его острых углов равна 90°. Поэтому ∠ ABD  = ∠ OBD  = 90° − 25° = 65°. Углы  ABD  и  ACD  опираются на одну дугу, поэтому эти углы равны. Таким образом, ∠ ACD  = 65°.

?

25°

Ответ: 65

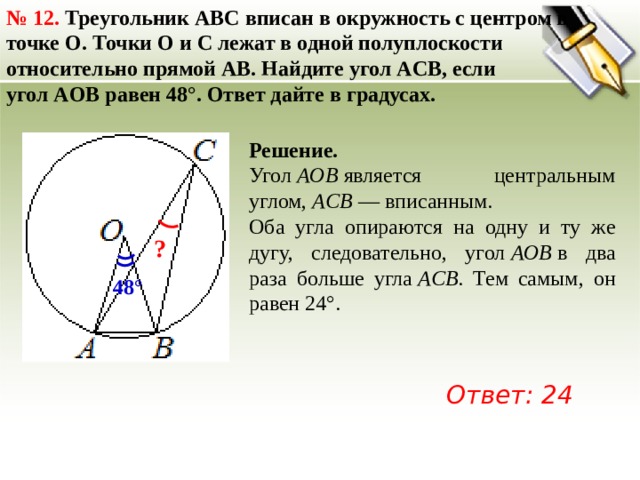
№  12. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 48°. Ответ дайте в градусах.

Решение.

Угол  AOB  является центральным углом,  ACB  — вписанным.

Оба угла опираются на одну и ту же дугу, следовательно, угол  AOB  в два раза больше угла  ACB . Тем самым, он равен 24°.

?

48°

Ответ: 24

№ 13. Точка О — центр окружности, ∠AOB = 84°. Найдите величину угла ACB (в градусах).

Решение.

Вписанный угол  ACB  равен половине центрального угла  AOB , опирающегося на ту же дугу, поэтому он равен 42°.

?

84°

Ответ: 42

№ 14. На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 63. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги АВ равна х .

х

63

дуга

в градусах

меньшая

в единицах

28 о

большая

длины

360 о - 28 о

63

х

28°

Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 747

№  15. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что 

∠ NBA=38°. Найдите угол NMB. Ответ дайте в градусах.

Решение.

Угол  NBA  — вписанный, поэтому он равен половине дуги, на которую он опирается. Следовательно, дуга  AN  = 2∠ NBA  = 2 · 38° = 76°. Диаметр  AB  делит окружность на две равные части, поэтому величина дуги  ANB  равна 180°. Откуда дуга  NB  = 180° − 76° = 104°.

Угол  NMB  — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен 104° : 2 = 52°.

38°

?

Ответ: 52

№  16. Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 15° и ∠OAB = 8°. Найдите угол BCO. Ответ дайте в градусах.

Решение.

Проведём радиус  OB .

8°

Рассмотрим треугольник  AOB :  AO  =  OB , следовательно, углы ∠ OAB  = ∠ ABO  = 8°.

∠ OBС  = ∠ ABC  − ∠ ABO  = 15° − 8° = 7°.

Рассмотрим треугольник  BOC :  BO  =  OC , следовательно, ∠ BCO  = ∠ OBC  = 15° − 8° = 7°.

15°

?

Ответ: 7

№  17. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 8,5. Найдите BC, если AC=8.

Решение.

Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол — прямой, и данный треугольник является прямоугольным. По теореме Пифагора получаем :

8

?

8,5

8,5

Ответ: 15

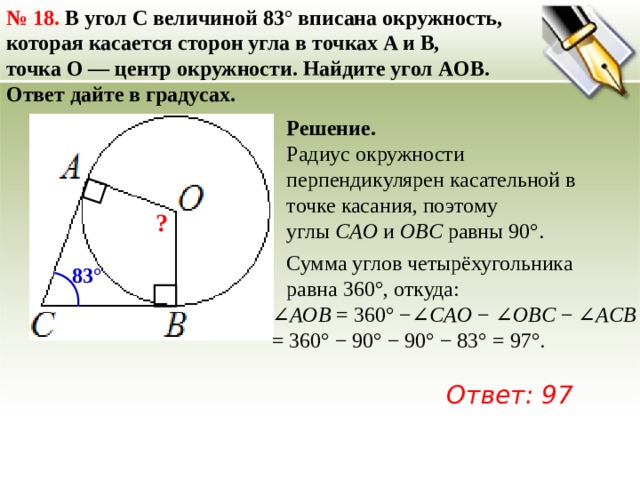
№  18. В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B,

точка O — центр окружности. Найдите угол AOB.

Ответ дайте в градусах.

Решение.

Радиус окружности перпендикулярен касательной в точке касания, поэтому углы  CAO  и  OBC  равны 90°.

?

Сумма углов четырёхугольника равна 360°, откуда:

83°

∠ AOB  = 360° −∠ CAO  − ∠ OBC  − ∠ ACB  

= 360° − 90° − 90° − 83° = 97°.

Ответ: 97

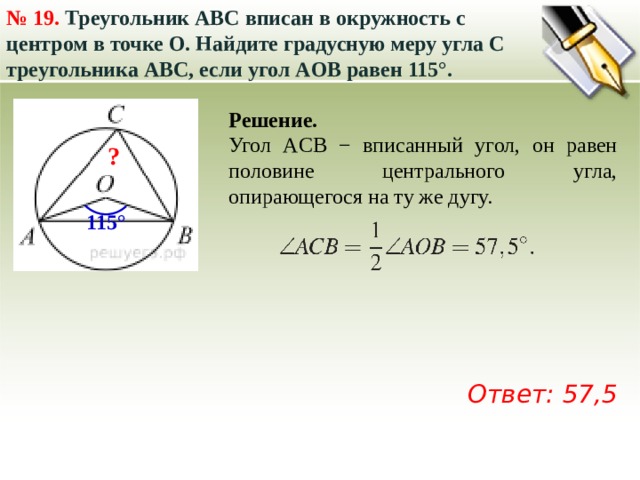
№ 19. Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 115°.

Решение.

Угол ACB − вписанный угол, он равен половине центрального угла, опирающегося на ту же дугу. 

?

115°

Ответ: 57,5

№  20. Сторона AC треугольника ABC содержит центр описанной около него окружности. Найдите , если

. Ответ дайте в градусах.

Решение.

Сторона AC треугольника ABC содержит центр описанной около него окружности AC — диаметр окружности.

- вписанный и опирается на полуокружность  AC   ∠АВС = 90°

Треугольник АВС - прямоугольный.

75°

?

Сумма острых углов прямоугольного треугольника равна 90°.

Значит,

Ответ: 15

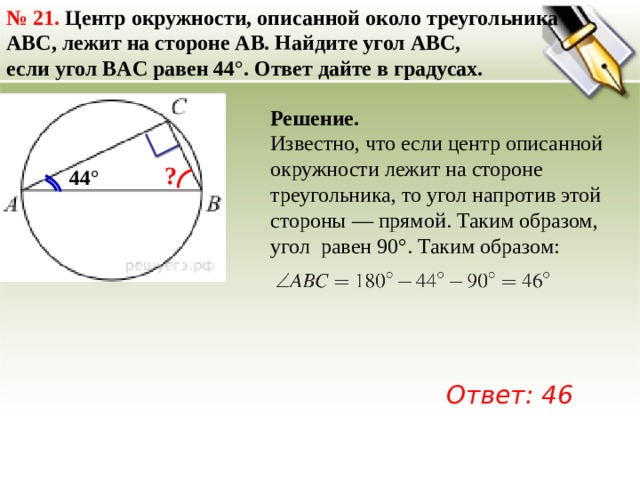
№  21. Центр окружности, описанной около треугольника 

ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 44°. Ответ дайте в градусах.

Решение.

Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол равен 90°. Таким образом:

?

44°

Ответ: 46

№  22. На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый.

Найдите угол ABC. Ответ дайте в градусах.

Решение.

Пусть точка O — центр окружности.

Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°.

О

Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол  OBC  прямой, то угол  ABC  = 90° − 54° = 36°.

Ответ: 36

№  22. На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый.

Найдите угол ABC. Ответ дайте в градусах.

Решение.

Угол между касательной и хордой

равен половине угловой величины

дуги, заключенной между ними.

Ответ: 36

Какие из следующих утверждений верны?

1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

2) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность не пересекаются.

3) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.

4) Около всякого треугольника можно описать не более одной окружности.

5) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.

6) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

7) Около любого ромба можно описать окружность.

8) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

9) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

Ответ: 1, 3, 4, 6, 8, 9 .