ГАПОУ «Оренбургский областной медицинский колледж»
Методическая разработка
для преподавателя
по дисциплине БД.04 МАТЕМАТИКА
«Обратные и сложные функции»
Оренбург – 2019
Рассмотрено и одобрено
на заседании ПЦК
общеобразовательных дисциплин
Протокол № ___ от «__»_______
Председатель ПЦК
_________________ Н.В. Лапина
Автор:
Е.В. Данилова, преподаватель математики высшей квалификационной категории.
Аннотация:
Методическая разработка предназначена для преподавателей математики.
Содержит план занятия, конспект занятия, список источников информации.
В разработке предложены различные формы работы студентов и методы контроля знаний и умений.
Содержание
| Технологическая карта занятия………………………………………………………. Ход занятия……………………………………………………………………………... Список источников…………………………………………………………………….. | 4 6 10 |
Технологическая карта занятия
Тема: Обратные и сложные функции.
Вид занятия: теоретическое занятие.
Тип занятия: изучение нового.
Цели:
Образовательные:
Знать: Функции. Область определения и множество значений. График функции. Обратная и обратимая функции. Область определения и область значений обратной функции. График обратной функции. Вертикальные и горизонтальные асимптоты графиков. Симметрия относительно прямой у = х. Сложная функция (композиции).
Уметь: определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения.
поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения.
Развивающие: Развивать память, логическое мышление, умение анализировать, систематизировать, проводить аналогии, делать выводы.
Воспитательные: Способствовать развитию потребности к самообразованию; саморазвитию. Воспитывать аккуратность и дисциплинированность.
Методическая: Ввести понятие обратной и обратимой функций. Отметить связь области определения и множества значений взаимно обратных функций и их графиков. Ввести понятие сложной функции (композиции).
Опорные понятия, термины: Функции. Область определения и множество значений. График функции. Обратная и обратимая функции. Область определения и область значений обратной функции. График обратной функции. Вертикальные и горизонтальные асимптоты графиков. Симметрия относительно прямой у = х. Сложная функция (композиция).
Межпредметные связи: физика.
Внутрипредметные связи: элементарные функции и их свойства, преобразования графиков функции, производная и первообразная функции.
Формы контроля: устный (фронтальный опрос), решение задач.
Методы: словесные, практические, наглядные, алгоритмизации.
Оснащение:
Методическое: рабочая программа, тематическое планирование, Федеральный компонент государственного стандарта среднего общего образования, план занятия.
Дидактическое: учебник «Алгебра и начала математического анализа 10-11».
Литература: Алимов Ш. А., Колягин Ю.М., Ткачёва М.В. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровень). Просвещение, 2018г.
Оборудование: доска классная, мел, линейка.
СВР: Арифметические операции над функциями.
Этапы занятия:
Организационный этап (1-2 мин).
Постановка цели и задач занятия. Мотивация учебной деятельности учащихся (2-3 мин).
Актуализация знаний (5-7 мин).
Изучение новой темы (60-65 мин).
Первичная проверка понимания (10-12 мин).
Рефлексия, подведение итогов занятия (2-3 мин).
Домашнее задание (1-2 мин).
План занятия
Организационный этап (1-2 мин).
Проверка готовности студентов к занятию. Проверка присутствующих.
Постановка цели и задач занятия. Мотивация учебной деятельности учащихся (2-3 мин).
Сообщение темы, целей, задач и плана занятия. Обоснование важности изучаемой темы.
Актуализация знаний (12-15 мин).
Фронтальный опрос на знание основных понятий темы «Функции и их графики».
Нахождение области определения функции и множества значений.
Симметрия относительно осей координат.
Изучение новой темы (55-60 мин).
Обратимая функция.
Обратная функция.
Область определения и множество значений взаимно обратных функций.
График обратной функции.
Сложная функция.
Первичная проверка понимания (7-10 мин).
Рефлексия, подведение итогов занятия (2-3 мин).
Домашнее задание (1-2 мин).
§7, № 131(четные), 132(2,3).
Ход занятия
Актуализация знаний
Вопросы фронтального опроса:
Что называется функцией?
Что такое область определения функции?
Что такое множество значений функции?
Что такое асимптота графика функции?
Какую функцию мы называем монотонной?
Какая функция называется возрастающей на интервале?
Какая функция называется убывающей на интервале?
Задание: Найти область определения функции.
а)  ; б)
; б) 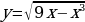
Задание: Найти множество значений функции.
а) 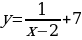 ; б)
; б) 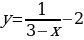
Задание: Отразить график функции, заданной графически, симметрично относительно: а) оси абсцисс; б) начала координат.
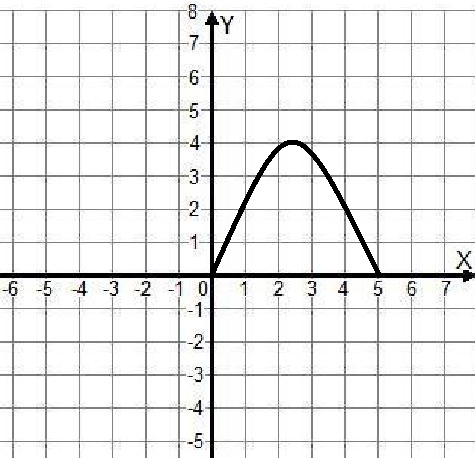
Изучение новой темы
Обратимая функция
Рассмотрим функции 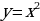 и
и 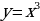 и их графики.
и их графики.


Вторая функция каждое свое значение у она принимает только в одной точке х, в отличие от первой, которая принимает каждое свое значение у в двух точках х, за исключением одной точки (вершины). Про первую функцию говорят, что она не обратима, а про вторую - обратима.
Определение: Если функция 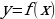 принимает каждое свое значение только при одном значении х, то эту функцию называют обратимой.
принимает каждое свое значение только при одном значении х, то эту функцию называют обратимой.
Теорема: Монотонная функция является обратимой.
Обратная функция
Пусть имеется обратимая функция 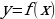 . Тогда каждому значению у из множества значений функции соответствует единственное значение х из ее области определения, такое что
. Тогда каждому значению у из множества значений функции соответствует единственное значение х из ее области определения, такое что  . Это соответствие определяет функцию х от у, которую обозначим
. Это соответствие определяет функцию х от у, которую обозначим  . В этой зависимости в соответствии с принятыми обозначениями поменяем местами х и у. Получим
. В этой зависимости в соответствии с принятыми обозначениями поменяем местами х и у. Получим 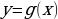 .
.
Функцию 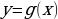 называют обратной к функции
называют обратной к функции 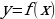 .
.
Исходную функцию и обратную ей называют взаимно обратными.
Пример: Найти функцию, обратную к функции:
а)  б)
б) 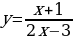
Решение: 


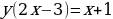
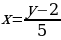
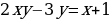

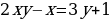

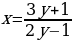

Ответ: а)  ; б)
; б)  .
.
Область определения и множество значений взаимно обратных функций
Из определения обратной функции следует, что область определения обратной функции совпадает со множеством значений исходной функции, а множеством значений обратной функции совпадает с областью определения исходной функции.
График обратной функции
Построим в одной системе координат графики функции  и обратной ей.
и обратной ей.
Найдем область определения исходной функции.
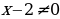

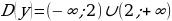 .
.
Составим таблицу значений исходной функции.
| X | -2 | -1 | 0 | 1 | 3 | 4 | 5 |
| Y | -1/4 | -1/3 | -1/2 | -1 | 1 | 1/2 | 1/3 |
Построим ее график.
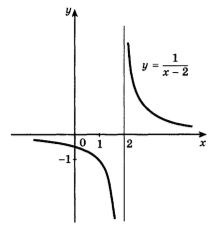
Следуя алгоритму нахождения обратной функции, получим функцию 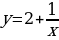 .
.
Ее область определения  . Составим таблицу значений.
. Составим таблицу значений.
| X | -1/3 | -1/2 | -1 | 1/3 | ½ | 1 | 2 |
| Y | -1 | 0 | 1 | 5 | 4 | 3 | 2,5 |

Если проведем прямую y=x, то можно заметить, что графики взаимно обратных функций симметричны относительно этой прямой.
Теорема: Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой y=x.
Сложная функция
Мы часто в повседневной речи считаем слова “сложный” и “трудный” синонимами. Иногда можно услышать от тех учеников, которым нелегко дается математика, что сложная функция потому так называется, что она “трудная”. Но на самом деле “сложный” и “трудный” далеко не всегда означают одно и то же.
Сложная функция – это композиция функций, т.е. функция от функции.
Сложная функция это когда одна функция (внутренняя) находится внутри другой функции (внешней), т.е. аргументом функции является другая функция.
Пример сложной функции:
y = (x + 2)5
Выражение x + 2 – это функция. Но эта функция в нашем примере возводится в 5-ю степень, т.е. над функцией есть ещё одна функция.
Чтоб увидеть вот эту внешнюю функцию обозначим x + 2 через t, получаем: y = t5 (вот так выглядит внешняя функция).
Но t сама является функцией, т.е. у нас функция оказалась под знаком другой функции.
Сложную функцию обычно представляют так (формула сложной функции): y = f (g(x)).
Здесь x находится под знаком функции g, а функция g находится под знаком функции f. Одна функция оказалась внутри другой, стала аргументом другой функции, это и есть сложная функция.
Итак, если аргументом функции является другая функция, то мы имеем дело со сложной функцией.
Первичная проверка понимания
№ 131 (нечетные)
№ 132 (1,4)
№ 133 (5)
Задайте формулами элементарные функции f и g, из которых составлена сложная функция h(x)=f(g(x)).
h(x)=(2x+1)7
б) h(x)=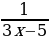
Домашнее задание
§7, №131 (четные),№132 (2,3)
СВР: Арифметические операции над функциями.
Список источников
Алимов Ш. А., Колягин Ю.М., Ткачёва М.В. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровень). Просвещение, 2018г.
Муравин Г.К., Муравина О.В. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый уровень). 10 класс. Дрофа, 2015г.
Никольский С.М., Потапов М.К., Решетников Н.Н. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровень). 10 класс. Просвещение, 2018г.
Интернет-ресурсы
http://school-collection.edu.ru/catalog/teacher/
http://www.school.edu.ru/

 Получите свидетельство
Получите свидетельство Вход
Вход












 Обратная и сложная функция (252.29 KB)
Обратная и сложная функция (252.29 KB)
 0
0 173
173 0
0 Нравится
0
Нравится
0


