Международная научно-практическая конференция
студентов и учащихся
«Наука и культура: новый взгляд»
Секция: математика
Удивительная лента Мёбиуса
Исследовательская работа
Выполнила: ученица 8 класса
МБОУ «СОШ им. Г.Г.Гарифуллина
с. Ядыгерь» Кукморского района РТ
Башарова Фирюза Маратовна.
Научный руководитель: учитель
математики Файзрахманова Г.З.
2016 год
Содержание
Введение………………………………………………………………………3
1. Мёбиус Август Фердинанд………………………………………………..5
2. Открытие Мебиуса…………………………………………………………6
3. Свойства листа Мебиуса…………………………………………………..8
4. Уравнения листа Мебиуса………………………………………………...11
5. Подобные объекты………………………………………………………...12
6. Применение листа Мебиуса
6.1. Лист Мебиуса в науке и технике……………………………………...13
6.2. Лист Мебиуса живописи и архитектуре……………………………...13
6.3. Лист Мебиуса в литературе и цирковом искусстве………………….14
6.4. Лист Мебиуса в искусстве……………………………………………..15
7. Задачи………………………………………………………………………16
8. Наши опыты……………….……………………………………………….17
Выводы ………………………………………………………………………..23
Заключение………………………………………………................................24
Список использованной литературы……………………………………….. 25
Введение
Для многих людей математика является и трудной, и непонятной, и неинтересной. Современник Сухомлинский считал, «что чувство удивления – могучий источник желания знать: от удивления к знаниям – один шаг». А математика замечательный предмет для удивления. Одним из таких предметов является лента Мебиуса.
Интересность ленты заключается уже в том, что в отличие от обыкновенного листа бумаги она имеет только одну поверхность, а не две. То есть, если начать закрашивать лист бумаги, не переходя через грань, то закрасится только одна сторона. Если проделать то же самое с лентой Мебиуса, лента закрасится с обеих сторон.
Загадки продолжаются, и когда мы начинаем разрезать ленту Мёбиуса. Лист Мёбиуса служил вдохновением для скульптур и для графического искусства.
Нас так заинтересовал этот лист, что мы стали искать про него разную информацию и проводить с ним разные опыты, о результатах которых я расскажу в своей работе.
Отсюда, объект исследования: лист Мёбиуса как модель односторонней поверхности. Предмет исследования: свойства односторонний поверхности на примере ленты Мёбиуса
Цель работы:
-определить и опытно – экспериментальным путём проверить удивительные свойства ленты Мёбиуса.
В соответствии с поставленной целью и выдвинутой гипотезой определились следующие задачи:
- раскрыть понятие топологии;
-изучить вклад А.Ф. Мёбиуса в развитие науки топологии;
- описать лист Мёбиуса и процесс его изготовления;
- показать использование листа Мёбиуса в искусстве;
- разработать методику определения удивительных свойств листа Мёбиуса;
- проверить опытно-экспериментальным путём эти свойства.
Метод исследования: практический эксперимент.
Теоретическая значимость нашей работы в том, что в последнее столетие большое влияние на ряд совершенно различных областей знания приобрела новая ветвь геометрии - топология. В наше время эта наука бурно развивается и находит применение в различных областях. Однако ей не уделяется должного внимания в школьном курсе геометрии.
1. Мёбиус Август Фердинанд
Одним из великих геометров XIX столетия был Август Фердинанд Мёбиус(1790-1868) - немецкий математик и астроном - теоретик. Родился 17 ноября 1790 года на территории княжеской школы Шульпфорте, близ Наумбурга (Саксония-Анхальт). Его отец занимал в этой школе должность учителя танцев. Мать Мёбиуса была потомком Мартина Лютера. Отец умер, когда мальчику было всего три года. Начальное образование Мёбиус получил дома и сразу показал интерес к математике. С 1803 по 1809 годы учился в колледже Шульпфорте, затем поступил в Лейпцигский университет. Первые полгода, в соответствии с рекомендациями семьи, он изучал право, но затем принял окончательное решение посвятить жизнь математике и астрономии. В 1813—1814 годах Мёбиус жил в Гёттингене, где посещал университетские лекции Гаусса по астрономии. Затем он уехал в Халле, чтобы прослушать курс лекций математика Иоганна Пфаффа, учителя Гаусса. В результате Мёбиус получил глубокие знания по астрономии и математике. Когда Мёбиус работал над докторской (1815 год), была сделана попытка призвать его в прусскую армию. С трудом, избежав этой угрозы, он успешно получил докторское звание. Математические исследования Мёбиуса принесли ему известность в научном мире. В 1848 году Мёбиус становится директором обсерватории.
2. Открытие Мебиуса
В 1858 году в возрасте шестидесяти восьми лет Мебиус представил Парижской академии мемуары об «односторонних» поверхностях. В своей работе «Об объёме многогранников» он описал геометрическую поверхность, обладающую совершенно невероятным свойством: она имеет только одну сторону! Семь лет он дожидался рассмотрения своей работы и, не дождавшись, опубликовал ее результаты.
Что же подтолкнуло Мебиуса к этому открытию? Есть три версии:
Открыть свой «лист» Мёбиусу помогла служанка, сшившая однажды неправильно концы ленты.
2. Придумал ленту Мёбиус, когда наблюдал за горничной, неправильно одевшей на шею свой платок.
3. Виноват во всём портной, который неправильно вшил манжет рубашки
Позже эта поверхность была названа лентой Мебиуса. В 1868 году Август Фердинанд Мёбиус умирает. Статья о знаменитой ленте Мёбиуса опубликована посмертно.
Одновременно с Мёбиусом изобрел этот лист и другой ученик К. Ф. Гаусса — Иоганн Бенедикт Листинг (1808— 1882), профессор Геттингенского университета. Свою работу он опубликовал на три года раньше, чем Мёбиус,— в 1862 году.
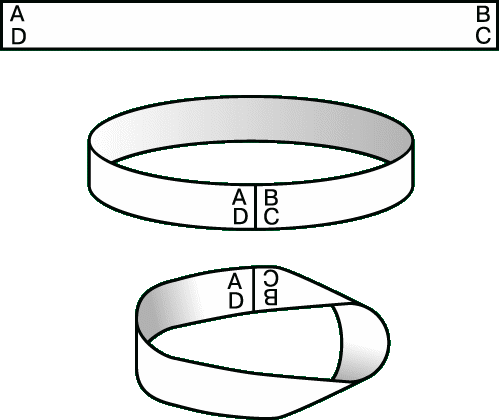
Что же это за поверхность – лента Мебиуса? Самое удивительное то, что сделать её своими руками совсем несложно: надо лишь взять полоску бумаги и склеить её концы, предварительно повернув один из них на 180о. И тогда в ваших руках окажется лист, или лента Мёбиуса. (Приложение №1)
Таинственный и знаменитый лист Мёбиуса имеет удивительные свойства: он имеет один край; одну поверхность. Действительно, начав закрашивать лист с любого места, можно убедиться, что постепенно вся поверхность будет закрашена. “Если на внутреннюю сторону обычного кольца посадить паука, а на наружную – муху и разрешить ползать как угодно, запретив лишь перелезать через края кольца, то паук не сможет добраться до мухи, не так ли? (Приложение№2) А если их обоих посадить на лист Мёбиуса, то бедная муха будет съедена, если конечно, паук ползает быстрее. Так изучение свойств именно этой поверхности во многом положила начало развитию новой ветви геометрии – науки топологии. В Вашингтоне у входа в Музей истории и техники установлен вращающийся монумент этой поверхности – стальной ленты закрученной на полвитка.
Лист Мёбиуса - один из объектов топологии. Интересно, что с точки зрения топологии гайка, макаронина и кружка - одинаковые объекты. Их роднит то, что каждый из них имеет одно и только одно отверстие. Если бы мы из пластилиновой гайки, не разрывая и не склеивая пластилин, захотели вылепить макаронину или кружку, то нам бы это удалось. А вот кастрюлю с двумя ручками уже не вылепить (в ней две дырки-ручки).Среди букв русского алфавита тоже есть топологически одинаковые буквы. (Приложение№3)
Чудесные свойства ленты Мебиуса породили множество фантастических рассказов. В одном из них описывался случай в Нью-Йоркском метро, когда потерялся во времени поезд, отправившийся в путь по сути, замкнутом в ленту Мебиуса. А в рассказе известного писателя-фантаста Артура Кларка «Стена Мрака» один из героев совершает путешествие по необычной планете, изогнутой в виде листа Мебиуса.
Физики пришли к выводу, что наша Вселенная вполне вероятно замкнута в ту же самую ленту согласно теории относительности Эйнштейна и его предположением, что космический корабль, всё время летящий прямо, может вернуться к месту старта, что подтверждает неограниченность и конечность Вселенной, изогнутой в пространстве большого числа измерений.
3. Свойства листа Мебиуса
Какими же свойствами обладает этот замечательный лист? (Прилож. №4)
1)Возьмем карандаш и начнем закрашивать ленту в каком-нибудь направлении. Вскоре мы вернемся в то место, откуда начали. Закрашенной оказалась вся лента целиком! А ведь мы ее не переворачивали, чтобы закрасить с другой стороны. Да и не смогли бы перевернуть, даже если бы очень захотели. Потому как поверхность ленты Мёбиуса - односторонняя. Такое вот любопытное свойство!
Что же из этого свойства следует? А следуют удивительные превращения ленты, если разрезать ее вдоль. При разрезании точно посередине, мы получили большое перекрученное кольцо. А вот если разрезать ленту на расстоянии 1/3 ее ширины от края, то получаются два кольца - но! - одно большое и сцепленное с ним маленькое. Если же разрезать еще и маленькое кольцо вдоль посередине, то получаются переплетенные два кольца - одинаковых по размеру, но разных по ширине. Другие интересные комбинации лент могут быть получены из лент Мёбиуса с двумя или более полуоборотами в них. Например, если разрезать ленту с двумя полуоборотами, то получится два одинаковых кольца, сцепленных между собой. Если разрезать ленту с тремя полуоборотами, последовательно два раза, то получится четыре кольца, сцепленных между собой. Разрез ленты Мёбиуса с дополнительными оборотами даёт неожиданные фигуры, названные парадромными кольцами.
2)Второе свойство – непрерывность. На листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом не придётся переходить через край «ленты». Разрывов нет – непрерывность полная.
3)Еще одно интересное свойство – связность. Если квадрат разрезать бритвой от стороны к стороне, то он распадётся на два отдельных куска. Точно также любой удар ножом разделит яблоко на две части. Но вот чтобы располовинить кольцо, нужно уже два разреза. И два раза придётся резать бублик, если вы хотите угостить им двух друзей. Поэтому любой тополог скажет вам, что квадрат– односвязен, кольцо и оправа от очков – друсвязны, а всяческие решётки, диски с отверстиями и подобные сложные фигуры – многосвязны. Ну, а лист Мёбиуса? Конечно двусвязен, т.к. если разрезать его вдоль, он превратится не в два отдельных кольца, а в одну целую ленту. Если перекрутить ленту на два оборота, то лист становится односвязным. Три оборота – связность снова равна двум. Связность принято оценивать числом Бетти, названным так в честь известного итальянского математика и физика. Иногда пользуются другой величиной – эйлеровой характеристикой – с той же целью: определить число сквозных, от края и до края, разрезов, которое выдерживает фигура, не распадаясь при этом на части.
4)Ориентированность - это то, чего нет у листа Мёбиуса! Вообразите, что в нём заключён целый плоский мир, где есть только два измерения, а его обитатели – несимметричные рожицы, не имеющие, как и сам лист никакой толщины. Если эти несчастные создания пропутешествуют по всем изгибам листа Мёбиуса и вернутся в начальную точку, то в изумлении обнаружат, что превратились в своё собственное зеркальное отображение. Конечно, всё это случится только, если они живут в листе, а не на нём.
5)«Хроматический номер». Он равен максимальному числу областей, которые можно нарисовать на поверхности так, чтобы каждая из них имела общую границу со всеми другими. Если каждую такую область выкрасить по-разному, то любой цвет должен соседствовать с любым другим. Лист Мёбиуса находит многочисленные применения в науке, технике и изучении свойств Вселенной. Есть гипотеза, что спираль ДНК сама по себе является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того - такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение или аннигиляция, как подтверждают физики. Они, кстати, утверждают также, что все оптические законы основаны на свойствах ленты Мебиуса, в частности отражение в зеркале - это своеобразный перенос во времени, краткосрочный, длящийся сотые доли секунды, ведь мы видим перед собой зеркального своего двойника. В ритмологическом ключе знак ленты Мёбиуса приобретает иное наполнение. Мы знаем, что есть ритмы, благодаря которым мы развиваем своё энергетическое, сердечное начало, и есть ритмы, обеспечивающие раскрытие нашего мозга, наших информационных возможностей. Чтобы эти противоположные начала развивались в нас равновелико и гармонично, между «энерго» - ритмами и «информо» - ритмами разместились ритмы Мёбиусного вихря. Благодаря им, мы имеем возможность непрерывно и бесконечно перемещаться от сердца к мозгу, от информации к энергии, сохраняя при этом баланс между планетарной и человеческой сторонами жизни. Ритмы Мёбиусного вихря позволяют нам совершать своеобразный «обмен» энергии на информацию и наоборот.
4. Уравнения листа Мебиуса
Параметрическое описание листа Мёбиуса. (Приложение №5)
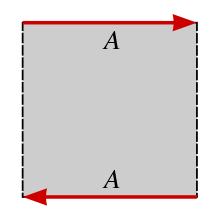
Чтобы превратить квадрат в лист Мёбиуса, соедините края, помеченные ![]() так, чтобы направления стрелок совпали.
так, чтобы направления стрелок совпали.
Одним из способов представления листа Мёбиуса как подмножества ![]() является параметризация:
является параметризация:
![]()
![]()
![]()
где ![]() и
и ![]() . Эти формулы задают ленту Мёбиуса ширины 1, чей центральный круг имеет радиус 1, лежит в плоскости x − y с центром в
. Эти формулы задают ленту Мёбиуса ширины 1, чей центральный круг имеет радиус 1, лежит в плоскости x − y с центром в ![]() . Параметр u пробегает вдоль ленты, в то время как v задает расстояние от края.
. Параметр u пробегает вдоль ленты, в то время как v задает расстояние от края.
В цилиндрических координатах ![]() , неограниченная версия листа Мёбиуса может быть представлена уравнением:
, неограниченная версия листа Мёбиуса может быть представлена уравнением:
![]()
где функция логарифма имеет произвольное основание.
5. Подобные объекты
1. Бутылка Клейна
Близким "странным" геометрическим объектом является бутылка Клейна — (определённая не ориентируемая поверхность). Бутылка Клейна может быть получена путём склеивания двух лент Мёбиуса по краям. В обычном трёхмерном евклидовом пространстве сделать это, не создавая самопересечения, невозможно.
Бутылка Клейна — это определённая неориентируемая поверхность. Бутылка Клейна впервые была описана в 1882 г. немецким математиком Феликсом Христианом Клейном. Она тесно связана с лентой Мёбиуса. Если разрезать бутылку Клейна пополам вдоль её оси симметрии, то результатом будет лента Мёбиуса. В отличие от обычной бутылки бутылка Клейна не имеет края, а еe поверхность нельзя разделить на внутреннюю и наружную. Та поверхность, которая кажется наружной, непрерывно переходит в ту, которая кажется внутренней, как переходят друг в друга две, на первый взгляд различные.
2. Поверхность Кипенского
Односторонняя поверхность А. В. Кипенского (Приложения№6)
Поверхность Кипенского получается из трёх цилиндрических полосок бумаги, склеенных последовательно друг с другом. То, что поверхность односторонняя, видно из среднего рисунка, обход по синей линии возвращает к этой точке с другой стороны бумаги, хотя линия не переходит через край. Интересно, что если поверхность разрезать по красным линиям, она разбивается на две зеркально-симметричные части. Одна из них показана на нижнем рисунке. Такой вариант поверхности был придуман А. В. Кипенским
6. Применение листа Мебиуса.
6.1. Лист Мёбиуса в науке и технике
Существовали технические применения ленты Мёбиуса.
Патентная служба зарегистрировала немало изобретений, в основе, которых лежит всё та же односторонняя поверхность. В 1923 году выдан патент изобретателю Ли де форсу, который предложил записывать звук на киноленте без смены катушек, сразу с двух сторон. Придуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания.
В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса. В 1971 году изобретатель с Урала Чесноков П.Н. применил фильтр в виде листа Мёбиуса. Полоса ленточного конвейера выполнялась в виде ленты Мёбиуса, что позволяло ему работать дольше, потому что вся поверхность ленты равномерно изнашивалась.
В матричных принтерах красящая лента имела вид листа Мёбиуса для увеличения срока годности. Также в системах записи на непрерывную плёнку применяются ленты Мёбиуса (чтобы удвоить время записи).
Устройство под названием резистор Мёбиуса — это недавно изобретённый электронный элемент, который не имеет собственной индуктивности.
Благодаря ленте Мебиуса появился "Механизм управления", на который получено Авторское свидетельство №1453110 (Приоритет 26.07.1985, автор Смирнов В.Б.). Механизм управления можно применить в детских заводных игрушках, в конструкции стабилизатора штурвала рулевого привода, в щелевом затворе фото- или кинокамеры.
В 2003 году японские учёные смогли получить в лабораторных условиях односторонние кристаллы в форме мёбиусной ленты.
6.2. Лист Мёбиуса в живописи и архитектуре
У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка. В 1967 году, когда в Бразилии состоялся международный математический конгресс, его устроители выпустили памятную марку достоинством в пять сентаво. На ней была изображена лента Мёбиуса. И монумент высотой более чем в два метра, и крохотная марка – своеобразные памятники немецкому математику и астроному Августу Фердинанду Мёбиусу, профессору Лейпцигского университета (Прил. №5).
6.3. Лист Мёбиуса в литературе и цирковом искусствеБолее 100 лет лист Мёбиуса используется для показа различных фокусов и развлечений. Удивительные свойства листа демонстрировались даже в цирке, где подвешивались яркие ленты, склеенные в виде листов Мёбиуса. Фокусник закуривал сигарету и горящим концом дотрагивался до средней линии каждой ленты, которая была выполнена из калийной селитры. Огненная дорожка превращала первую ленту в более длинную, а вторую - в две ленты, продетая одна в другую. (В этом случае фокусник разрезал лист Мёбиуса не посередине, а на расстоянии в одну треть его ширины).
Фокусники используют лист Мебиуса уже на протяжении 75 лет. Вот пример еще одного фокуса: фокусник вручает зрителю три больших бумажных кольца, каждое из которых получилось путем склеивания концов длинной ленты. Зритель разрезает ножницами первое кольцо вдоль ленты посередине, пока не вернется в исходную точку. В результате получаются два отдельных кольца. Разрезая таким же образом второе кольцо, он получает, к своему удивлению, не два кольца, а одно, которое вдвое длиннее исходного. Наконец, разрезая третье, он снова получает поразительный результат: два кольца, сцепленных друг с другом. Результат этого фокуса зависит от того, как были сомкнуты концы ленты перед склейкой. Первое наше кольцо получилось путем простого соединения концов ленты без перекручивание. Второе кольцо получается при соединении концов ленты, перекрученной один раз на 180ْ. Третье кольцо получилось при разрезании ленты, концы которой перекручивались перед склейкой дважды. Известно еще много фокусов с применением ленты Мебиуса.
6.4. Лист Мёбиуса в искусстве
Лист Мёбиуса служил вдохновением для скульптур и для графического искусства. Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных, показывает муравьев, ползающих по поверхности листа Мёбиуса.
Лист Мёбиуса также постоянно встречается в научной фантастике, например в рассказе Артура Кларка «Стена Темноты». Иногда научно-фантастические рассказы (вслед за физиками-теоретиками) предполагают, что наша Вселенная вполне вероятна, замкнута в ленту Мебиуса. Согласно теории относительности - чем больше масса, тем больше кривизна пространства.
Лист Мёбиуса иногда называют прародителем символа бесконечности, т.к. находясь на поверхности ленты Мёбиуса, можно было бы идти по ней вечно. Это не соответствует действительности, так как символ использовался для обозначения бесконечности в течение двух столетий до открытия ленты Мёбиуса.
Некоторые ломали головы над тем, как сделать ленту Мёбиуса неким «предком» символа бесконечности, ведь двигаться поверхностью ленты можно действительно вечно. Но этот факт себя не оправдал, так как данный символ существовал задолго до открытия Мёбиуса.
7. Задачи
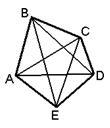
1)Каждые две из пяти произвольно заданных в плоскости точек A, B, C, D, E соединены прямой. Площади возникающих при этом пяти треугольников EAB,ABC, BCD, CDE, DEA заданы; требуется выразить через них площадь пятиугольника ABCDE.
Решение: вместо площадей этих пяти треугольников можно также считать заданными ![]() площади пяти четырёхугольников: BCDE, CDEA, DEAB, EABC, ABCD, — и искать выражение через них площади пятиугольника ABCDE (Приложение№7)
площади пяти четырёхугольников: BCDE, CDEA, DEAB, EABC, ABCD, — и искать выражение через них площади пятиугольника ABCDE (Приложение№7)
Площадь ![]() пятиугольника ABCDE у которого площади треугольников EAB, ABC, BCD, CDE, DEA равны соответственно a, b, c, d,e есть корень квадратичного уравнения
пятиугольника ABCDE у которого площади треугольников EAB, ABC, BCD, CDE, DEA равны соответственно a, b, c, d,e есть корень квадратичного уравнения
![]()
Не менее интересно и то, что площадь ![]() пятиугольника ABCDE, у которого площади четырёхугольников BCDE, CDEA, DEAB, EABC, ABCD равны соответственно
пятиугольника ABCDE, у которого площади четырёхугольников BCDE, CDEA, DEAB, EABC, ABCD равны соответственно ![]() есть корень "такого же" квадратного уравнения
есть корень "такого же" квадратного уравнения
![]()
Мёбиус рассматривает не только выпуклые многоугольники, но и учитывает что порядок, в котором следуют точки A, B, C и точки B, C, D, соответствует обходу по сторонам эти треугольников по часовой стрелке, а порядок, в котором следуют точки C, D, E— обходу по сторонам треугольника CDE против часовой стрелки. Более того, Мёбиус рассматривает не только "обычные" многоугольники, но и такие, у которых стороны могут пересекаться не только в вершинах многоугольника (рис.9).И как итог, можно сказать— если каждые две точки какой- либо системы и точек, расположенных в плоскости, соединить прямой линией, и если считать заданными площади (независимые между собой) каких-либо 2n-5 многоугольников , возникающих от пересечения этих прямых, то через них можно выразить площадь каждого из остальных многоугольников".
8. Наши опыты
| I опыт: | Поставили точку на одной стороне кольца и начертили непрерывную линию вдоль него. |
| II опыт: | Закрасили полностью только одну сторону колец. Раскрасили внутреннюю и внешнюю сторону обычного кольца разными красками. |
| III опыт: | Закрасили непрерывной линией только один край колец. Закрасили узенькую полоску края ленты. |
| IV опыт: | На внутреннюю сторону обычного кольца мысленно посадим зайца, а на наружную волка. Разрешим им бегать как угодно, запретив перелезать через края кольца. Посадим на ленту Мебиуса зайца и волка. Разрешим им бежать в разных направлениях. |
| V опыт: | Разрезали кольца пополам вдоль. (Чтобы проверить, какая поверхность получилась необходимо снова прочертить непрерывную линию.) |
| VI опыт: | Разрезали кольцо вдоль, отступив от края 1/3. (Чтобы проверить, какая поверхность получилась необходимо снова прочертить непрерывную линию.) |
| VII опыт: | Разрезали результат I опыта (уже разрезанную ленту) пополам вдоль. |
| VIII опыт: | Склеили ленту из квадрата или из прямоугольника, у которого стороны приблизительно равны, не сминая бумаги. |
| IX опыт: | Склеили ленту из квадрата или из прямоугольника, у которого стороны приблизительно равны, складывая бумагу. |
| X опыт: | Проводили опыты с многоразовым перекручиванием и разрезанием. |
Можно, конечно, провести еще немало опытов с перекручиванием ленты на четыре оборота, на пять, на шесть и с последующим разрезанием кольца вдоль посередине, и на расстоянии в 1/3 ширины от края, и в 1/4.
Но усложнение эксперимента часто не приводит к более эффектным результатам.
Результаты моих экспериментов с бумагой и экспериментальных исследований свойств ленты Мебиуса представлены в Таблице 1.
Таблица 1
| I |
| Поставили точку на одной стороне каждого кольца и чертили непрерывную линию вдоль него, пока не пришли снова в отмеченную точку | ||||||
| Обычное кольцо |
| Линия проходит вдоль кольца по одной стороне, сходясь в точке начала. Вторая сторона остается чистой | (Приложение№8) | |||||
| Лента Мебиуса |
| Непрерывная линия проходит по двум сторонам, заканчиваясь в начальной точке |
| |||||
| II |
| Закрасили полностью только одну сторону колец | ||||||
| Обычное кольцо |
| Одна сторона закрашена, другая – нет | (Приложение№9) | |||||
| Лента Мебиуса |
| Лента закрашена целиком |
| |||||
| III |
| Закрасили непрерывной линией только один край колец | ||||||
| Обычное кольцо |
| Один край кольца закрашен, второй край нет | (Приложение№10) | |||||
| Лента Мебиуса |
| Линия края получилась, непрерывно закрашена на всем кольце |
| |||||
| IV |
| На внутренней поверхности стоит заяц, а по внешней идет в любую сторону волк | ||||||
| Обычное кольцо |
| Заяц и волк никогда не встретятся, не пересекая края | (Приложение№11)
| |||||
| Лента Мебиуса |
| Заяц и волк встретятся, не пересекая края в любом случае | (Приложение№12) | |||||
| V |
| Разрезали кольца вдоль пополам, по линии параллельной краям | ||||||
| Обычное кольцо |
| Получилось два кольца, уже, чем исходное, причем длина окружности каждого будет такой же, как длина окружности первоначально взятого | (Приложение№13) | |||||
| Лента Мебиуса |
| Получилось одно кольцо в виде восьмёрки |
| |||||
| V.A |
| Для проверки: какая получилась поверхность, на полученных в опыте V кольцах необходимо провести непрерывную линию | ||||||
| Обычное кольцо |
| Непрерывная линия будет проходить только по одной стороне кольца |
| |||||
| Лента Мебиуса |
| Непрерывная линия будет проходить только по одной стороне кольца. (Получилась не лента Мебиуса) |
| |||||
| VI |
| Разрезали кольцо вдоль, отступив от края на 1/3 ширины кольца | ||||||
| Обычное кольцо |
| Получилось 2 кольца одно уже, другое шире | (Приложение№14) | |||||
| Лента Мебиуса |
| Получилось два сцепленных друг с другом кольца, одно маленькое – другое большое |
| |||||
| VI.A |
| Для проверки: какая получилась поверхность, на полученных в опыте VI кольцах необходимо провести непрерывную линию | ||||||
| Обычное кольцо |
| Непрерывная линия будет проходить только по одной стороне кольца |
| |||||
| Лента Мебиуса |
| Непрерывная линия будет проходить только по одной стороне большого кольца (не лента Мебиуса), по всей поверхности маленького кольца будет проходить линия с двух сторон (лента Мебиуса) |
| |||||
| VII |
| Разрезали результат V опыта (уже разрезанную ленту) пополам вдоль | ||||||
| Обычное кольцо |
| Получились отдельные кольца | (Приложение№15) | |||||
| Лента Мебиуса |
| Получилось два больших кольца, переплетенные между собой в виде восьмерки |
| |||||
| VIII |
| Склеили ленту из квадрата или из прямоугольника, у которого стороны приблизительно равны не сминая бумаги | ||||||
| Обычное кольцо |
| Получилась «труба» |
| |||||
| Лента Мебиуса |
| Невозможно осуществить на практике, не сминая бумаги |
| |||||
| IX |
| Склеили ленту из квадрата или из прямоугольника, у которого стороны приблизительно равны складывая бумагу | ||||||
| Обычное кольцо |
| Получилась «труба» |
| |||||
| Лента Мебиуса |
| Получили ленту Мебиуса |
| |||||
| X |
| Проводили опыты с многоразовым перекручиванием и разрезанием (Приложение№16) | ||||||
Экспериментальные выводы
Итак, на основе проведенных мною теоретических и практических исследований можно сделать следующие выводы:
-Лента Мебиуса имеет 1 край.
-Лента Мебиуса имеет одну поверхность.
-Лента Мебиуса имеет одну искривленную поверхность, и если по ней двигаться, можно с внутренней части переместиться на внешнюю.
-Лист Мёбиуса - топологический объект. Как и любая топологическая фигура, лента Мёбиуса не меняет своих свойств, пока ее не разрезают, не разрывают, или не склеивают его отдельные куски.
-Один край и одна сторона листа Мебиуса не связаны с его положением в пространстве, не связаны с понятиями расстояния.
-Если закрашивать одну сторону ленты Мебиуса, не пересекая края, то в итоге закрасится вся поверхность ленты.
-Если пустить по поверхности ленты Мебиуса, движущиеся объекты, они будут двигаться бесконечно долго.
-Лента Мебиуса получается из прямоугольника, у которого длина намного больше ширины.
-Если допустить, что можно взять квадрат или прямоугольник любого размера и при этом можно сгибать бумажную поверхность, то мы сможем склеить ленту Мебиуса.
-Если разрезать ленту Мебиуса вдоль посередине параллельно краю, то можно получить не две отдельные ленты, а одну длинную ленту, которая будет уже исходной и дважды перекручена – но не лента Мебиуса.
Если разрезать ленту Мебиуса вдоль, отступив от края 1/3 ее ширины, то получится два кольца, сцепленные между собой, одно большое – не лента Мебиуса, другое маленькое – лента Мебиуса.
Также можно сделать такие эксперементы, как ниженаписанные
1) Завязать на шарфе узел, не выпуская из рук его концов.
( Это можно сделать так. Положите шарф на стол. Скрестите руки на груди. Продолжая держать их в таком положении, нагнитесь к столу и возьмите поочередно по одному концу шарфа каждой рукой. После того как руки будут разведены, в середине шарфа сам собой получится узел. Пользуясь топологической терминологией, можно сказать, что руки зрителя, его корпус и шарф образуют замкнутую кривую в виде “трехлистного” узла. При разведении рук узел только перемещается с рук на платок.)
2) Вывертывание жилета на изнанку, не снимая с человека.
(Владельцу жилета необходимо сцепить пальцы рук за спиной. Окружающие должны вывернуть жилет наизнанку, не разнимая рук владельца. Для демонстрации этого опыта необходимо расстегнуть жилет и стянуть его по рукам за спину владельца. Жилет будет болтаться в воздухе, но, конечно, не снимется, потому что руки сцеплены. Теперь нужно взять левую полу жилета и, стараясь не измять жилет, просунуть ее как можно дальше в правую пройму. Затем взять правую пройму и просунуть ее в ту же пройму и в том же направлении. Осталось расправить жилет и натянуть его на владельца. Жилет окажется вывернутым на изнанку
Выводы
Работая над этой темой я узнала много нового об известном учёном Мёбиусе и о его изобретениях. Лист Мёбиуса – первая односторонняя поверхность, которую открыл учёный. Позже математики открыли ещё целый ряд односторонних поверхностей. Но эта – самая первая, положившая начало целому направлению в геометрии, по – прежнему привлекает к себе внимание учёных, изобретателей, художников. В этой работе я пыталась описать свойства этой прекрасной поверхности-листа Мебиуса, показать его значимость на практике, доказать, что лист Мёбиуса – топологическая фигура.
Мы выяснили, что лист Мебиуса имеет один край, лист Мебиуса имеет одну сторону.
Лист Мёбиуса – топологический объект. Как и любая топологическая фигура лента Мёбиуса не меняет своих свойств, пока ее не разрезают, не разрывают или не склеивают его отдельные куски.
Главная ценность листа Мебиуса состоит в том, что он дал мощный толчок новым обширным математическим исследованиям
Лист Мёбиуса – первая односторонняя поверхность, которую открыл учёный. Позже математики открыли ещё целый ряд односторонних поверхностей. Но эта – самая первая, положившая начало целому направлению в геометрии, по – прежнему привлекает к себе внимание учёных, изобретателей, художников.
В этой работе мы пытались описать свойства этой прекрасной поверхности-листа Мебиуса, показать его значимость на практике, доказать, что лист Мёбиуса – топологическая фигура.
Мёбиус повлиял не только на математиков, но и на художников, скульпторов, архитекторов и многих, многих, многих… В результате появились картины, скульптуры, марки, наколки и прочие произведения искусства с изображение ленты Мёбиуса.
Я думаю, что следов Мёбиуса в искусстве будет ещё много.
Заключение
«Мышление начинается с удивления»,- заметил 2500 лет назад Аристотель. Наш современник Сухомлинский считал, «что чувство удивления – могучий источник желания знать: от удивления к знаниям – один шаг». А математика замечательный предмет для удивления.
Именно это мы попытались показать в своей работе, описывая лист Мёбиуса и процесс его изготовления, раскрывая опытным путём свойства этого поразительного открытия. Наше предположение подтвердилось: лента Мёбиуса обладает не только свойством односторонности, но и такими, действительно, неожиданными свойствами, как непрерывность и связность.
Удивительные свойства ленты Мёбиуса используются в самых различных изобретениях. Свойство односторонности листа Мебиуса было использовано в дизайне одежды и украшений, кулинарии, в химии, физике, технике, биологии. Если ременной передачи ремень сделать в виде листа Мебиуса, то его поверхность будет изнашиваться вдвое медленнее, чем у обычного кольца. Это дает ощутимую экономию. В матричных принтерах красящая лента также имела вид листa Мёбиуса для увеличения срока годности. В виде парадоксальной геометрической фигуры можно, оказывается, изготовить лопасти бетономешалки или обычного бытового миксера — энергозатраты снизятся на одну пятую, а качество бетона (или кондитерского крема) улучшится. Лист Мёбиуса применяют в велосипедной и волейбольной камере. Совсем недавно ей нашли другое применение - она стала играть роль особенной пружины в заводных игрушках. Такая пружина могла бы стать бесценной– её нельзя перекрутить, как обычную – своего рода вечный двигатель.
Работая над проектом, я пришла к выводу, что свойства, которыми обладает лента Мёбиуса можно использовать еще в швейной промышленности при оригинальном раскрое ткани, при автоматизации сельского хозяйства.
Список литературы:
Воронец А.М. Математические развлечения. М.: Учпедгиз, 1981.
Гарднер М. Математические досуги. М.: 1992.
Кордемский Б.А., Ахадов А.А. Удивительный мир чисел для учащихся. М.: Просвещение, 1996.
Кордемский Б.А. Топологические опыты своими руками./ «Квант» №3, 1974,стр73.
Коробенок Е.В., Столяр А.А. Сколько сторон у поверхности?: Беседы с учащимися VII-X классов. Минск: Народная асвета, 1995.
Леман И. Увлекательная математика. М.: Знание, 1985.
Лоповок Л.М. Математика на досуге: Книга для учащихся среднего школьного возраста (IV-VIII классы). М.: Просвещение, 1990.
Мубаракзянов Г.М.Математические символы и термины, история их возникновения. Казань: Изд-во “Фән” Академии наук Рт, 2008.
Рупасов К.А. Математика на школьной сцене. Тамбов, 1999.
Научно-популярный журнал "Квант" 1975год №7, 1977 №7.
10. Интернет – ресурсы:
http://websib.ru/noos/math/listmebiusa/index.html
http://canegor.urc.ac.ru/training/2/vozp.htm
http://host.km.ru/sashka/ho7/lenta.htm
| Приложения |
|
| Приложение №1
|
|
| Приложение №2
|
|
| Приложение№3
| |
| Приложение№4
|
|
| Приложения№5
|
|
| Приложения№6 |
|
| Приложение№7 |
|
| Приложение№8 |
|
| Приложение №9
| |
| Приложение№10
|
|
| Приложени№11
|
|
| Приложение№12
|
|
| Приложение№13
| |
| Приложение№14
| |
| Приложение№15
| |
| Приложение№16 |
26

 Получите свидетельство
Получите свидетельство Вход
Вход




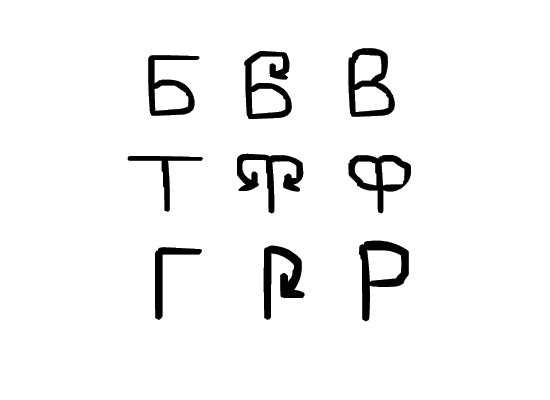













 Научная работа на тему "Удивительная лента Мебиуса" (534.5 KB)
Научная работа на тему "Удивительная лента Мебиуса" (534.5 KB)
 0
0 4714
4714 246
246 Нравится
0
Нравится
0


