Модульная педагогическая технология
на уроках математики
(из опыта работы учителя математики МБОУ Кировская СОШ Колохматовой О.В.)
Содержание:
Введение
Глава 1. Процесс планирования уроков на основе модульной педагогической технологии.
Глава 2. Структура проведения модульного практикума по теме «Линейные уравнения» в 6 классе
Заключение
Список литературы.
Приложения
Введение
Одним из положительных результатов обучения математики на сегодняшний день можно считать довольно широкую реализацию принципа дифференциации обучения. При дифференцированном обучении очень важно вести учет индивидуальных особенностей учащихся. Уровневую дифференциацию можно осуществлять и в модульной технологии, при этом каждый учащийся может определить свою «ступеньку» знаний.
Модульная технология в большей степени ориентирована на самостоятельную деятельность учащихся, которую они выполняют в течение определенного отрезка времени. В процессе самостоятельной деятельности учащийся анализирует свой «знаниевый» потенциал: а) умеет ли он воспроизводить решения по указаниям учителя (I уровень); б) делать выбор из имеющихся методов решения; в) находить выход из нестандартной ситуации. Такой самоанализ может сподвигнуть ученика либо серьёзнее заняться математикой, либо выйти за пределы учебника.
Глава 1. Процесс планирования уроков на основе модульной педагогической технологии.
Одной из главных целей применения на уроках модульной технологии является создание комфортного темпа работы для каждого ученика. Каждый ученик получает шанс определить свои возможности, уровень знаний, а также приспособиться к тем уровням изучения материала, которые предложены учителем.
Главным отличием данной технологии является применение принципа планирования совместной деятельности учителя и ученика.
На каждом этапе модуля определяются цели для учащихся, т.е. устанавливается, кто хочет знать не более того, что требуется государственным стандартом, а кто готов заниматься больше, поскольку планирует в будущем поступить в институт или просто получить высокую оценку. После того как учащиеся определились со своими целями, учитель выстраивает свое целеполагание, определяя содержание и объём педагогической помощи учащимся.
Исходя из целей проектируется итоговая диагностика. Она создается с учетом уровневой дифференциации, что позволяет учащимся осознанно определять тот минимум знаний, который необходим для получения оценки «3».
На основании целеполагания и планируемой итоговой диагностики отбирается предметное содержание (объяснения и задания из учебника, из дидактических материалов и т.д.).
На основании отобранного содержания выстраивается логика изучения темы (поурочное планирование), определяются время и место промежуточной и итоговой диагностик и учебной коррекции. Для каждого урока определяются микроцели учащихся и приемы обратной связи; создаются опорные конспекты для учащихся и задания к уроку.
В результате описанного процесса учитель создает:
логическую структуру уроков с промежуточной диагностикой;
разноуровневые материалы для диагностики знаний учащихся;
дидактический материал ко всем урокам.
Модульная педагогическая технология помогает осуществлять индивидуальный подход к учащимся, включать каждого в осознанную деятельность, мотивировать её, формировать навыки самообучения и самоорганизации, обеспечивая тем самым постепенный переход от пассивно воспринимающей позиции ученика к его сотрудничеству с учителем.
Глава 2. Структура проведения модульного практикума по теме «Решение уравнений» в 6 классе.
Рассмотрим пример проведения урока по данной технологии.
Целью изучения данного модуля является обобщение знаний и умений решать линейные уравнения, и распределяются по трем уровням: I уровень – самый общий, т.е. знаниями этого уровня должны овладеть все учащиеся, II уровень включает все, что достигнуто на I уровне, но в более сложном виде, а III уровень – все, что достигнуто на I и II уровнях, но теперь должно применяться в нестандартных ситуациях.
В результате овладения содержанием модуля учащиеся должны уметь:
I уровень – решать линейные уравнения по заданному алгоритму;
II уровень – решать линейные уравнения, самостоятельно выбирая метод решения;
III уровень – применять полученные знания в нестандартной ситуации.
Работа учащихся состоит из нескольких этапов, так называемых учебных элементов. Каждый учебный элемент содержит или указания учителя о том, что нужно знать и уметь, или краткие пояснения к выполнению заданий, а также список заданий. Вся работа над данным модулем сопровождается оценочным листом учащегося (см. Приложение 1).
Прочитав указания учителя, ученик выполняет самостоятельные работы, которые включены в учебный элемент, и проверяет их по эталонам решений. Эталон учитель демонстрирует ученику, когда тот объявляет о завершении самостоятельной работы. Ученик сравнивает свои ответы с эталонными и исправляет ошибки. Оценка за весь модуль зависит от суммы набранных баллов по всем учебным элементам.
Заключение
Математика является не только очень важным учебным предметом общеобразовательной школы, но и весьма сложным, так как математическими способностями обладают немногие школьники, а обучить математической грамоте необходимо всех. Для этого все средства хороши. И достижения учащихся во многом зависят не только от умения учителя преподать материал, но и во время дать учащемуся самому проанализировать свою учебную деятельность.
Библиографический список
Адрова,И.А., Ромашко,И.В. Модульный урок в X классе/ Математика в школе №4. – М.: Школа – пресс, 2001
Манвелов, К.Н. Конструирование современного урока математики.- М.: Просвещение, 2005. – 124 с.
Виленкин,Н.Я. Математика: учеб. для 6 кл. общеобразоват. учреждений. – М.: Просвещение, 2005. – 264 с.: ил.
Приложение 1.
Оценочный лист учащегося
| Ф.И. учащегося |
| Учебные элементы | Время выполнения задания | Выбранный уровень работы | Общее количество баллов за этап |
| №1 Входной контроль |
|
|
|
| №2 Решение линейных уравнений |
|
|
|
| №3 Решение уравнений с использованием основного свойства пропорции |
|
|
|
| №4 Решение уравнений с модулем |
|
|
|
| Итоговое количество баллов |
|
| №5 Выходной контроль |
|
| (Оценивается учителем) |
Приложение 2.
| УЭ - 0 |
Интегрирующая цель
|
|
| Продолжить формирование умений и навыков решения уравнений. Обобщение и систематизация алгоритмов и методов решений основных типов уравнений. Развитие навыков исследований в поисках приемов решений и их правильном оформлении. Развитие умений объективно оценивать свою работу.
|
| УЭ - 1 |
Входной контроль
|
|
| 1. Раскройте скобки и найдите значение выражения: а) -9,5 + (0,2 + 9,5) ; б) –(6,8 - 5,43) – 0,2; в) 3,15 – (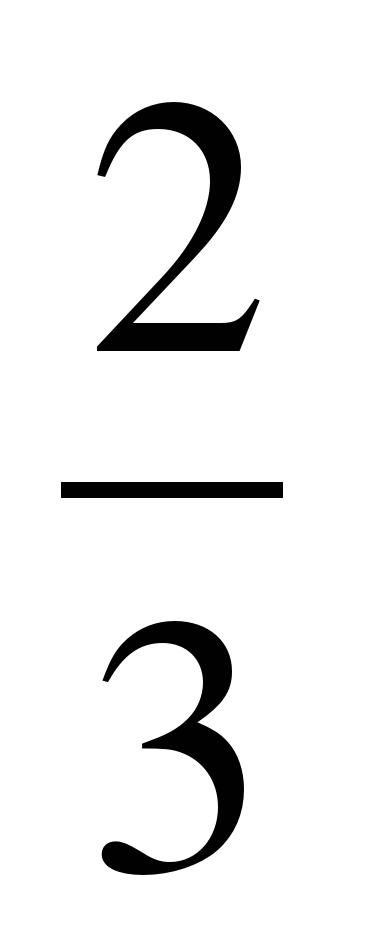 + 2,15) + 2,15)
2. Раскрой скобки а) 4(2с – 5); б) -3(а + 0,5); в) 12(-3у + 2х); г) -0,3(-5р – 2с)
3. Среди представленных выражений найдите сумму подобных слагаемых:
4с 0,3у -61 -3,6х у 9,5р -с 7ху 2,4х
| Работаем 5 мин. Каждое задание 1 балл. |
|
|
| УЭ - 2 |
Решение линейных уравнений
|
| 2.0 | Цель: проверить свои умения при решении линейных уравнений с помощью переноса слагаемых и умножения обеих частей уравнения на число. |
|
| 2.1 | Напомним правила при решении уравнений: Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и тоже число, не равное нулю. Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак. |
|
| 2.2

1 уровень

2 уровень | Решите самостоятельно.
1 вариант 2 вариант
Найдите корень уравнения  а) 6х – 12 = 5х + 4; а) -3у – 5 = 14у -22; а) 6х – 12 = 5х + 4; а) -3у – 5 = 14у -22; б) 5х + 8 = -4х – 1 б) -12р – 3 = 11р – 3
С помощью умножения обеих частей уравнения на одно и тоже число освободитесь от дробных чисел и решите уравнение:  а) а) 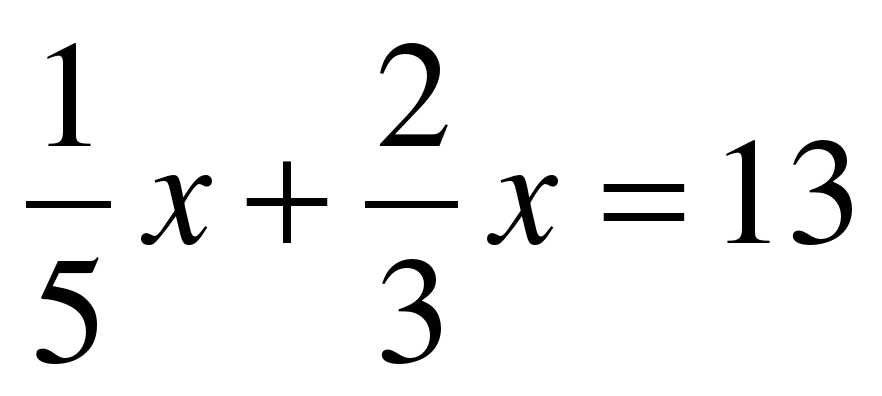 ; а) ; а) 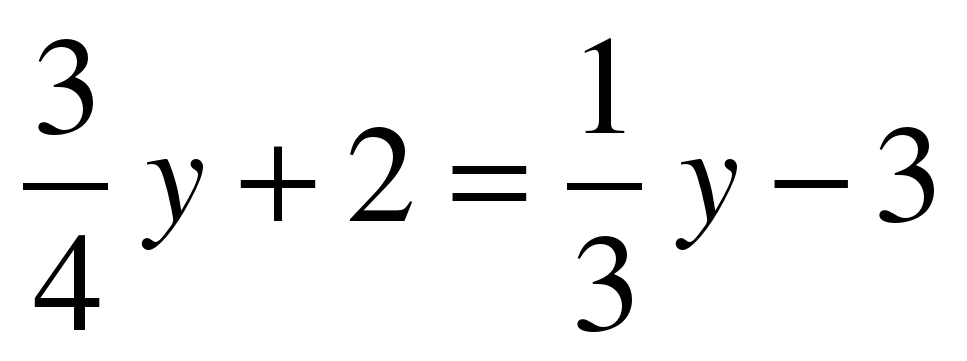 ; ; б) 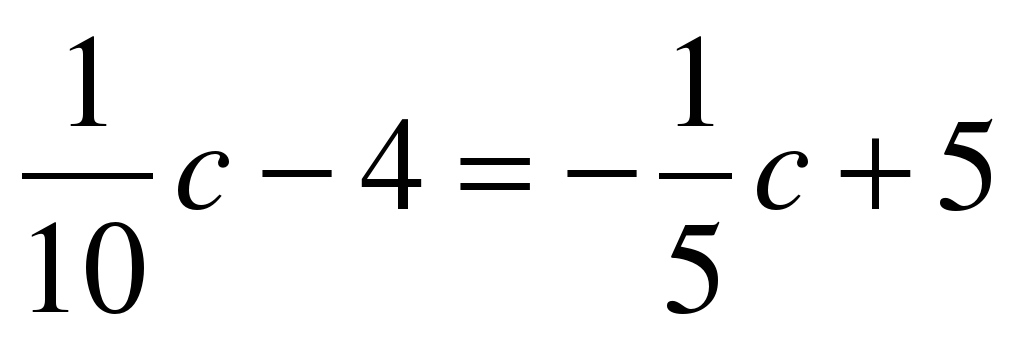 б) б) 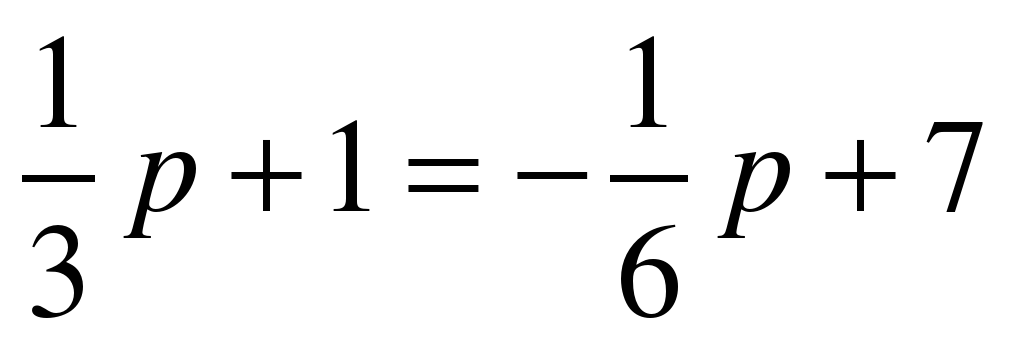
 Решите уравнение : Решите уравнение :
а) -20(х – 0,2) = 44 – (2х + 4); а) 0,4(у +5) = 5 – (7-1,4у) б) (3,6– 2с)∙ 3=-5 -2(-0,2с–1,1) б) -5(с – 3,4) = 0,8 -3(7-с)
Найдите корень уравнения:  а) а)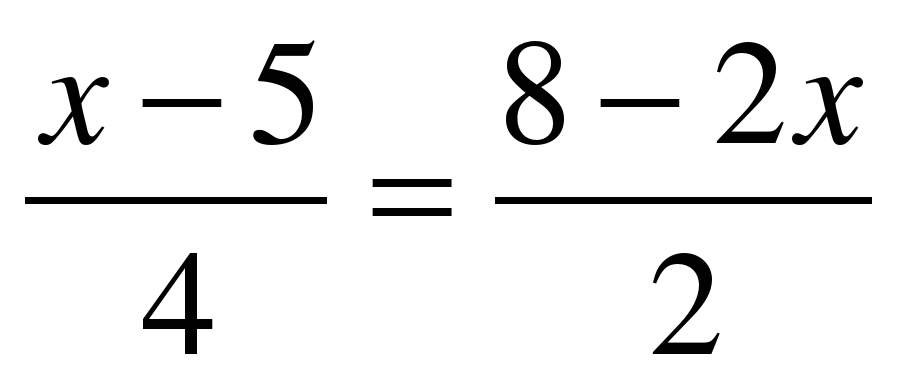 +1; а) +1; а) 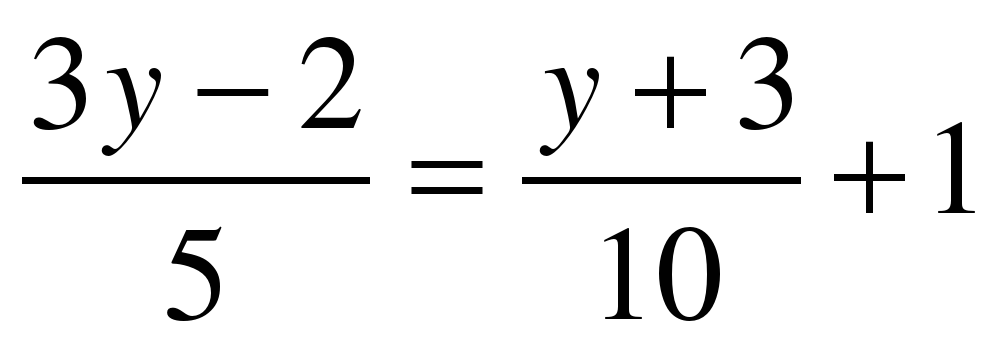 ; ; б) 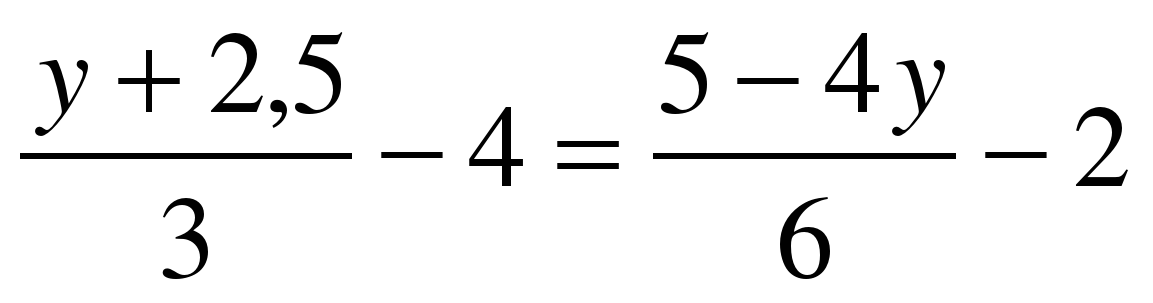 б) б) 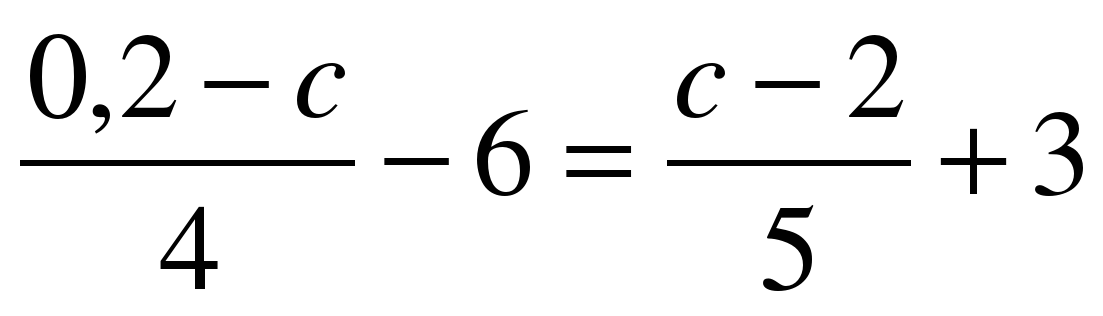
| Работаем 12 минут. Проверка по эталону на доске.
1балл 1 балл
2 балла
2 балла
2 балла 2 балла
2 балла
3 балла |
|
|
Оцените свою работу. Если возникли вопросы, задайте их учителю.
|
|
| УЭ - 3 |
Решение уравнений, с использованием основного свойства пропорции.
|
| 3.0 |
Цель: уметь правильно применить основное свойство пропорции при решении уравнений.
|
|
| 3.1 |
Напомним основное свойство пропорции: в верной пропорции произведение крайних членов равно произведению средних.
Пример: 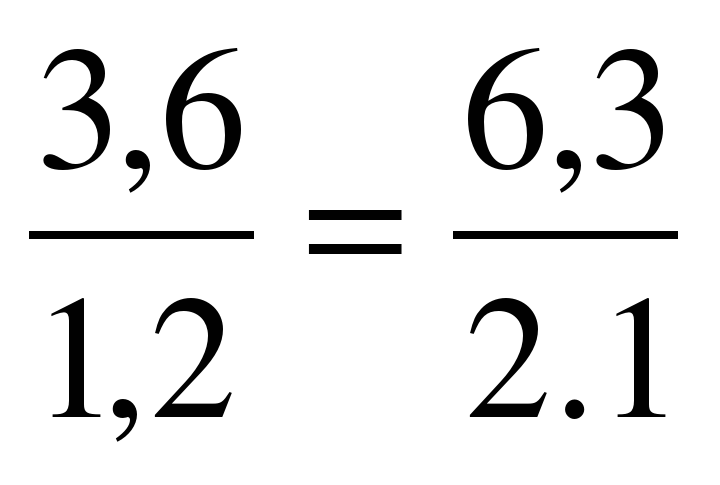 Найдем произведение её крайних и произведение её средних членов. Найдем произведение её крайних и произведение её средних членов. Получим 3,6 ∙ 2,1 = 6,3 ∙ 1,2 7,56 = 7,56
|
|
| 3.2 |
Решите самостоятельно уравнения (решить 2)  1 вариант 2 вариант 1 вариант 2 вариант
а) 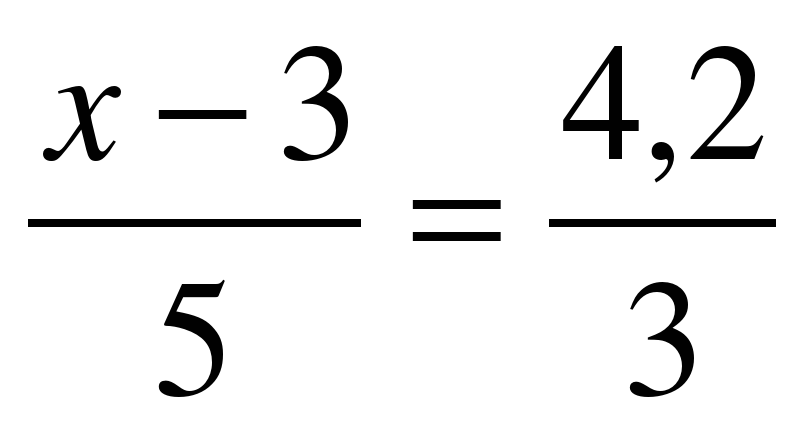 а) а) 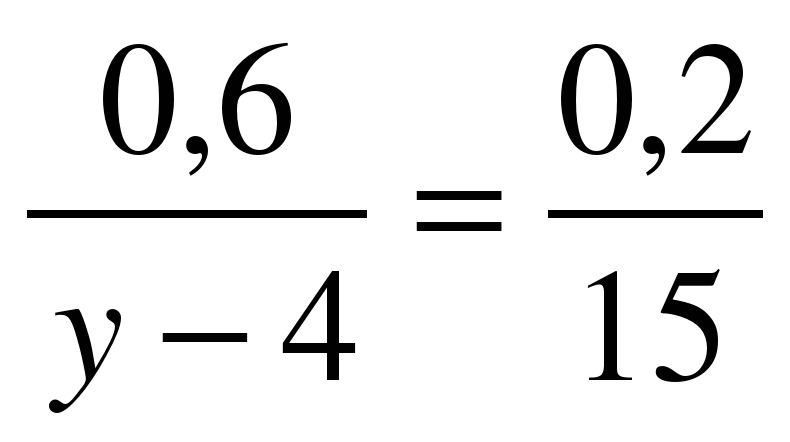 б) 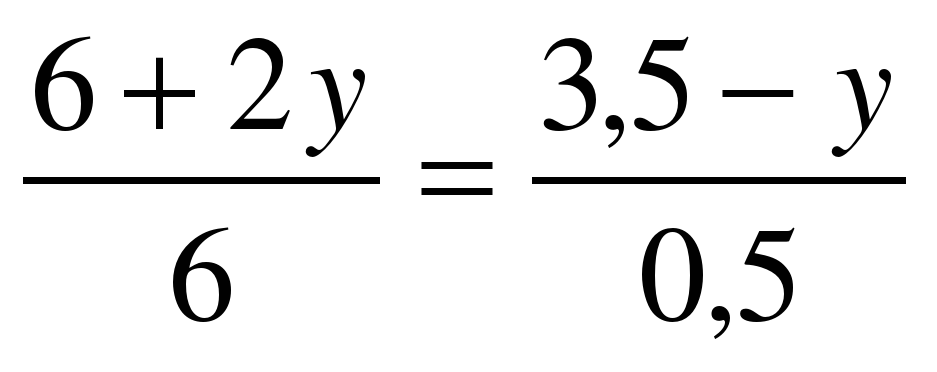 б) б) 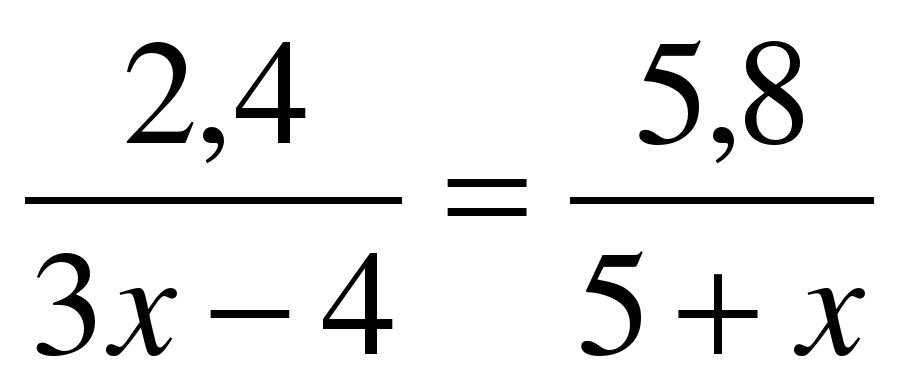 в) 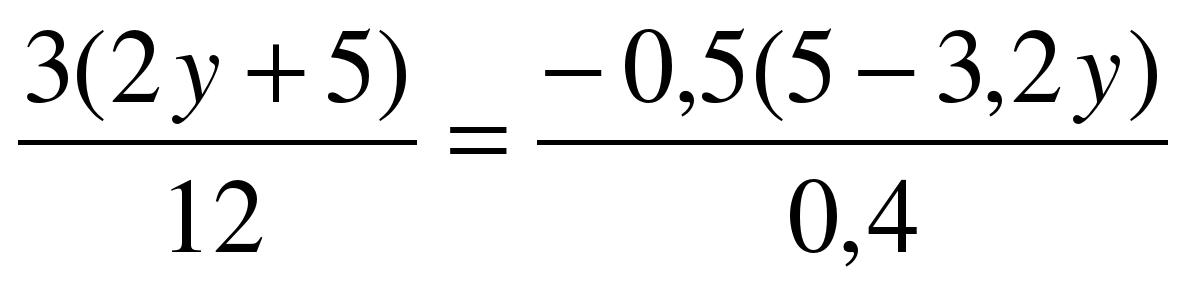 в) в) 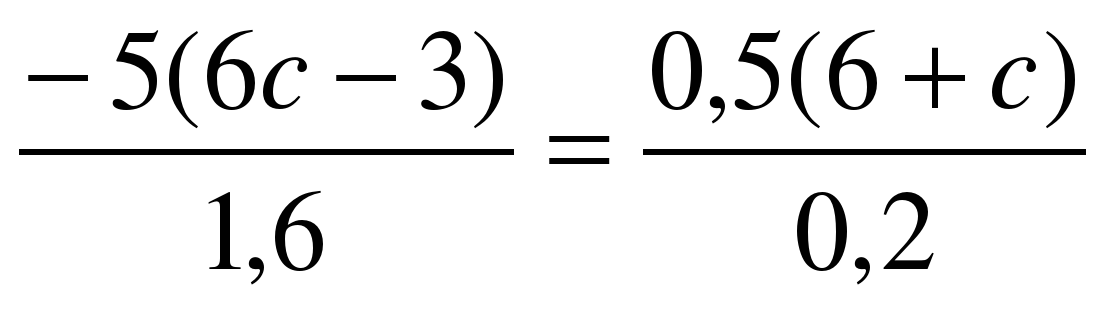
|
Работаем 10 минут.
1 балл
2 балла
3 балла |
|
|
Вернитесь к цели учебного элемента. Есть ли необходимость вернуться к какому-либо заданию? Оцените свою работу по достижению цели.
|
|
| УЭ - 4 |
Решение уравнений с модулем.
|
|
| 4.0 |
Цель: проверить и оценить умения применять знания о модуле при решении уравнений.
|
|
| 4.1 | Напомним теорию о модуле: Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а). Модуль числа 0 равен 0. Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного числа – противоположному числу.
Пример 1. | 7| = 7, |-5| = 5 Пример 2. Решить уравнение: | x | = 6 х = 6 или х = -6 Ответ: {6; -6} Пример 3. Решить уравнение: |x – 3| + 5 = 12 |x – 3| = 12 – 5 |x – 3| = 7 х – 3 = 7 или х – 3 = -7 х = 10 или х = -4 Ответ: {10; -4}
|
|
| 4.2

1 уровень

2 уровень | Решите самостоятельно.
1 вариант 2 вариант
а) |x – 5| = 2,5 а) |6 – x| = 12 б) 15 - |5 – 4y| = 3 б) 22 + |17 – 4y| = 28 в) |x + 3| +1 = 0 в) 13 - |x + 7| = 20
а) 43 - |x – 5| = 13 а) |7x – 1| -14 = 22 б) |5 – 2x| = x – 1 б) |3x + 5| = 5 – x в) |3y – 4| + 3 = 0 в) |3e + 1| +1 2 = 3
| В уровне 2(б) сделать проверку!
1 балл 2 балла 1 балл
2 балла 3 балла 1 балл |
|
|
Оцените свою работу. Если у вас есть вопросы, задайте их учителю.
|
Подсчитайте количество набранных вами баллов.
Если вы набрали 28 баллов, то вы молодцы, усвоили материал и можете выполнять более сложные задания.
Если вы набрали 21 – 27 баллов, то вам необходимо выполнить задания 1 уровня.
Если вы набрали менее 20 баллов (не расстраивайтесь, чуть больше усилий!), то вы должны выполнить задания 1 уровня.
| УЭ - 5 | Выходной контроль |
|

1 уровень

2 уровень | 1 вариант 2 вариант
Найдите корень уравнения: а) -4(-2р + 7) = р + 1,7 а) с – 32 = (4с + 12) – 5,2 б) б) в) в)
Решите уравнение с модулем: а) |2x – 4| -5 = 0 а) |3x + 12| -6 = 9 б) |x – 12| +4 = -4 б) 7 - |x – 3| = 7
Найдите корень уравнения:
а) -3(2,1m – 1)+4,8 = 6,7m-27,4 а) 0,8(2а – 6) = - 2(4а +3)
б) х : 3,5 = 1,2 :0,4 б) 2,5 :6,8 = 1,5 :х
в) в) Решите уравнение с модулем:
а) 12 - |x -3| = 2,5 -х а) 34,5 - |6y – 4| = 4,5+ х
б) |23 - |5+ x|| = 12 б) ||x+4| - 15| = 20
| Работаем 15 минут |
| УЭ - 6 |
Рефлексия
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход





 а) 6х – 12 = 5х + 4; а) -3у – 5 = 14у -22;
а) 6х – 12 = 5х + 4; а) -3у – 5 = 14у -22; а)
а)  Решите уравнение :
Решите уравнение : а)
а) 1 вариант 2 вариант
1 вариант 2 вариант










 Модульный практикум по математике "Решение уравнений" (0.12 MB)
Модульный практикум по математике "Решение уравнений" (0.12 MB)
 0
0 1014
1014 98
98 Нравится
0
Нравится
0


