Моделирование зависимостей между величинами

Моделирование зависимостей между величинами

к урокам информатики в 11 классе

Величины и зависимости между ними

Примеры зависимостей:

• время падения тела на землю зависит от его первоначальной высоты;
• давление газа в баллоне зависит от его температуры;
• уровень заболеваемости жителей города бронхиальной астмой зависит от концентрации вредных примесей в городском воздухе.

Реализация математической модели на компьютере требует владения приемами представления зависимостей между величинами.

Этапы построения зависимостей

• Выделение количественных характеристик исследуемого объекта:

• имя значение тип
• имя
• значение
• тип

• Определение качественных характеристик объекта (определение типа зависимости)

• функциональная (формула) статистическое прогнозирование корреляционная зависимость оптимальное планирование …
• функциональная (формула)
• статистическое прогнозирование
• корреляционная зависимость
• оптимальное планирование
• …

• Построение модели

• математическая модель табличная модель графическая модель
• математическая модель
• табличная модель
• графическая модель

• Отображение зависимости

• формула таблица график (диаграмма)
• формула
• таблица
• график (диаграмма)

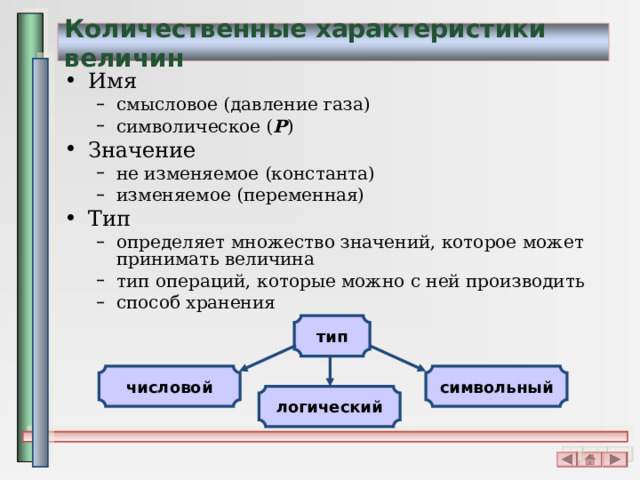
Количественные характеристики величин

• Имя

• смысловое (давление газа) символическое ( P )
• смысловое (давление газа)
• символическое ( P )

• Значение

• не изменяемое (константа) изменяемое (переменная)
• не изменяемое (константа)
• изменяемое (переменная)

• Тип

• определяет множество значений, которое может принимать величина тип операций, которые можно с ней производить способ хранения
• определяет множество значений, которое может принимать величина
• тип операций, которые можно с ней производить
• способ хранения

тип

числовой

символьный

логический

Падение тела

t (с) – время падения

H (м) – высота падения

Зависимость будем представлять, пренебрегая учетом сопротивления воздуха.

Ускорение свободного падения g (м/с 2 ) будем считать константой.

Значение H однозначно определяет значение t (функциональная зависимость).

Давление газа

P ( H/ м 2 ) – давление газа

t ( ° С) – температура газа

Давление при нуле градусов P 0 будем считать константой для данного газа.

Значение t однозначно определяет значение P (функциональная зависимость).

Математическая модель

• совокупность количественных характеристик некоторого объекта (процесса) и связей между ними, представленных на языке математики.

Падение тела

Давление газа

Функциональная зависимость

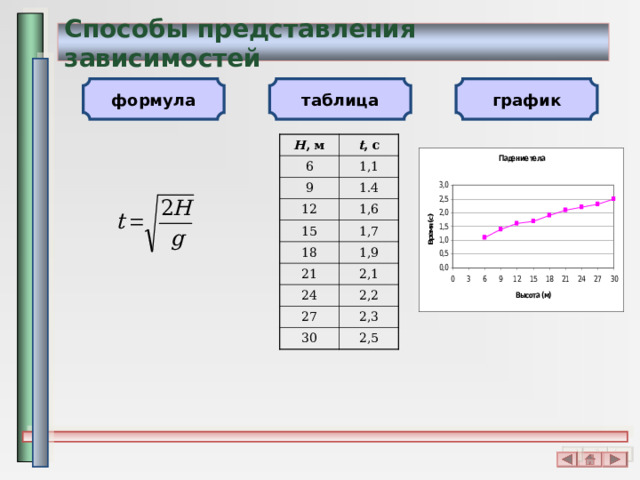
Способы представления зависимостей

график

формула

таблица

H , м

t , с

6

1 ,1

9

1.4

12

1,6

15

1,7

18

1,9

21

2,1

24

2,2

27

30

2,3

2,5

, м

, с

Динамические модели

• информационные модели. которые описывают развитие систем во времени.

В физике : описывают движение тел

В биологии : развитие организмов и популяций животных

В химии : протекание химических реакций

Домашнее задание

• § 17, № 2, 3.

02.02.23